✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
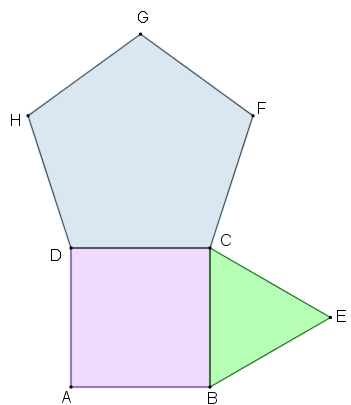
A figura abaixo mostra um triângulo equilátero, um quadrado e um pentágono regular.
Determinar a soma em graus das medidas dos ângulos [tex]E\hat{A}D[/tex] e [tex]E\hat{F}D[/tex].
Solução
(1) Inicialmente, observe que o triângulo e o pentágono são regulares e ambos têm um lado em comum com o quadrado (que é um quadrilátero regular).
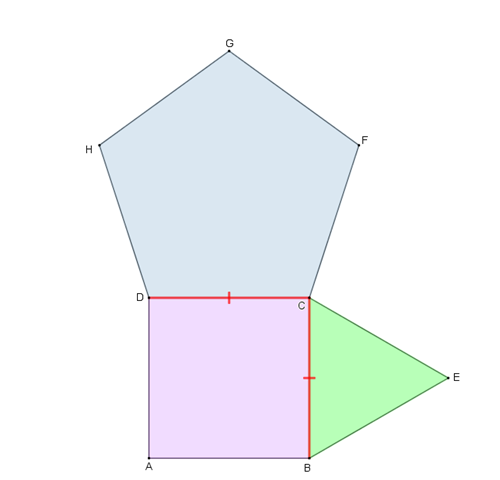
- Assim, os lados do triângulo, do pentágono e do quadrado têm todos o mesmo comprimento.
(2) Vamos determinar a medida [tex]\alpha \, [/tex], em graus, do ângulo [tex]E\hat{A}D[/tex].
- Como [tex]BCE[/tex] é um triângulo equilátero, a medida do ângulo [tex]E\hat{B}C[/tex] é [tex] 60^\circ[/tex].
- Como [tex]ABCD[/tex] é um quadrado, o ângulo [tex]A\hat{B}C[/tex] mede [tex]90^\circ[/tex].
- A aresta [tex]BC[/tex] é comum ao quadrado e ao triângulo, donde [tex]AB=BE[/tex] e, portanto, o triângulo [tex] ABE[/tex] é isósceles.
- A medida do ângulo [tex]E\hat{B}A [/tex] é dada por [tex] 60^\circ + 90^\circ = 150^\circ[/tex].
- Como a soma dos ângulos internos de um triângulo é igual a [tex]180^\circ[/tex] e o triângulo [tex] ABE[/tex] é isósceles, temos que a medida de [tex]E\hat{A}B[/tex] é
[tex]\qquad \dfrac{180^\circ-150^\circ}{2}=15^\circ[/tex].
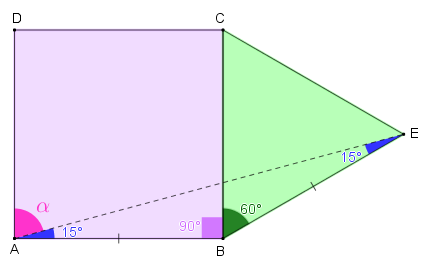
Assim, a medida de [tex]E\hat{A}D[/tex] é a diferença entre as medidas dos ângulos [tex]D\hat{A}B \, [/tex] e [tex] \, E\hat{A}B [/tex] e, dessa forma,
[tex]\hspace{3cm}\boxed{\alpha=90^\circ – 15^\circ = 75^\circ} \, .\qquad \textcolor{#800000}{(i)}[/tex]
(3) Agora, vamos determinar a medida [tex]\beta \, [/tex], em graus, do ângulo [tex]E\hat{F}D[/tex].
- Como o pentágono [tex]DCFGH[/tex] é regular, [tex]D\hat{C}F=108^\circ[/tex]. (Se você não sabe como justificar esse resultado, clique AQUI).
- Observando os ângulos em torno do vértice [tex]C[/tex] vemos que a medida do ângulo [tex]E\hat{C}F [/tex] pode ser assim obtida:
[tex]\qquad 360^\circ – (108^\circ + 90^\circ + 60^\circ)=102^\circ[/tex]. - Perceba que o triângulo [tex]FCE[/tex] é isósceles; logo, os seus ângulos da base têm a mesma medida. Como a soma dos ângulos internos de um triângulo é [tex]180^\circ[/tex], podemos então concluir que a medida do ângulo [tex]E\hat{F}C[/tex] é:
[tex]\qquad \dfrac{180^\circ-102^\circ}{2}=\dfrac{78^\circ}{2}= 39^\circ[/tex]. - O triângulo [tex]FCD[/tex] também é isósceles e a medida do ângulo [tex]C\hat{F}D[/tex] pode ser assim calculada:
[tex]\qquad \dfrac{180^\circ-108^\circ}{2}=\dfrac{72^\circ}{2}=36^\circ[/tex].
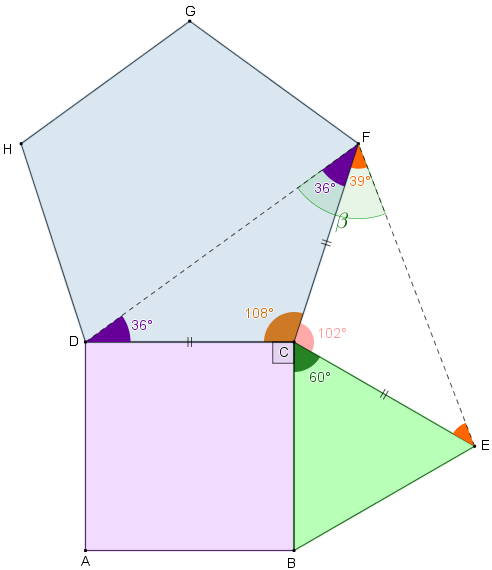
Portanto:
[tex]\hspace{3cm}\boxed{\beta=39^\circ + 36^\circ = 75^\circ} \, .\qquad \textcolor{#800000}{(ii)}[/tex].
Por [tex]\textcolor{#800000}{(i)} \, [/tex] e [tex] \, \textcolor{#800000}{(ii)}[/tex], concluímos que os ângulos [tex]E\hat{A}D[/tex] e [tex]E\hat{F}D[/tex] têm a mesma medida e a soma das duas medidas solicitada no problema é [tex] \, \fcolorbox{black}{#eee0e5}{$75^\circ+75^\circ=150^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
