✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
Considerando que [tex]x\, [/tex] e [tex]\, y[/tex] são números reais, resolva o seguinte sistema de desigualdades:
[tex] \begin{cases}
y\lt 3x+6 \\
x \gt -3 \\
y \leqslant 2
\end{cases}.[/tex]
Solução
Perceba que dos pares ordenados de números reais [tex](x,y)[/tex] tais que [tex]x \gt -3\, [/tex] e [tex]y \leqslant 2[/tex] teremos que determinar quais satisfazem a desigualdade [tex]y\lt 3x+6\, .[/tex]
Algebricamente não conseguimos exibir todos os pares ordenados que satisfazem as três desigualdade; conseguimos apenas trocar "seis por meia dúzia " e escrever que a solução [tex]S[/tex] do sistema de desigualdades em questão é:
[tex]S=\{\, (x,y) \in \mathbb{R}\times \mathbb{R}\, |\, x \gt -3\, ,\, y \leqslant 2 \text{ e }\, y\lt 3x+6\, \}\, .[/tex]
Dessa forma, vamos exibir " geometricamente " todas as soluções, analisando uma a uma as três desigualdades.
Vamos lá!
- Sabemos que a reta [tex]r[/tex] definida por [tex]x = -3\, [/tex] divide um plano cartesiano [tex]xOy[/tex] em três regiões disjuntas:
- Sabemos que a reta [tex]s[/tex] definida por [tex]y = 2\, [/tex] divide um plano cartesiano [tex]xOy[/tex] em três regiões disjuntas:
– os pontos [tex](x,y)[/tex] que estão sobre a reta [tex]s\, [/tex],
– os pontos [tex](x,y)[/tex] que estão acima da reta [tex]s\, [/tex],
– os pontos [tex](x,y)[/tex] que estão abaixo da reta [tex]s\, [/tex]. - Sabemos, também, que a reta [tex]t[/tex] definida por [tex]y= 3x+6\, [/tex] divide um plano cartesiano [tex]xOy[/tex] em três regiões disjuntas:
– os pontos [tex](x,y)[/tex] que estão sobre a reta [tex]t\, [/tex],
– os pontos [tex](x,y)[/tex] que estão acima da reta [tex]t\, [/tex],
– os pontos [tex](x,y)[/tex] que estão abaixo da reta [tex]t\, [/tex].
– os pontos [tex](x,y)[/tex] que estão sobre a reta [tex]r\, [/tex],
– os pontos [tex](x,y)[/tex] que estão à direita da reta [tex]r\, [/tex],
– os pontos [tex](x,y)[/tex] que estão à esquerda da reta [tex]r\, [/tex].
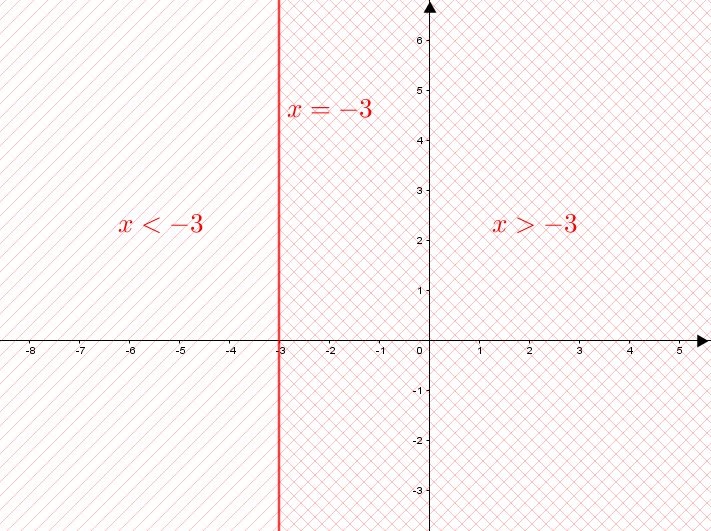
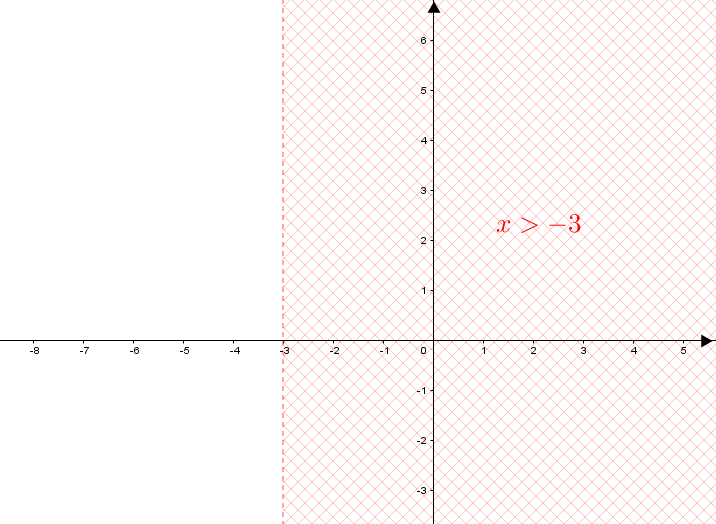
Para atender à desigualdade [tex]x \gt -3\, [/tex], nos interessam os pontos que estão à direita de [tex]r\, .[/tex]
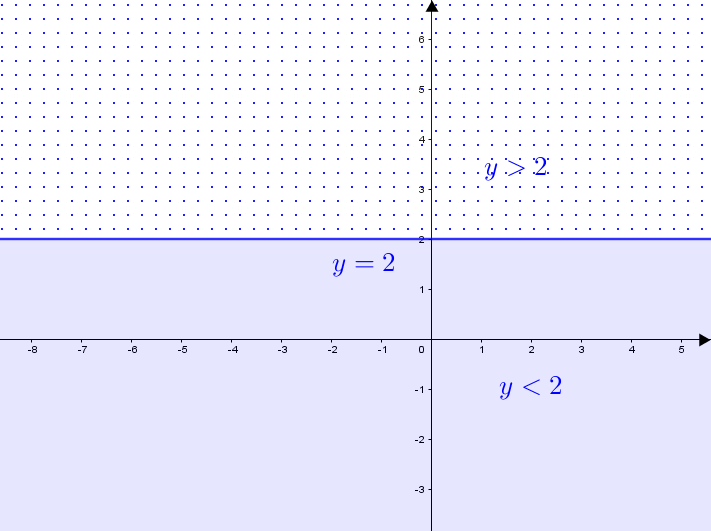
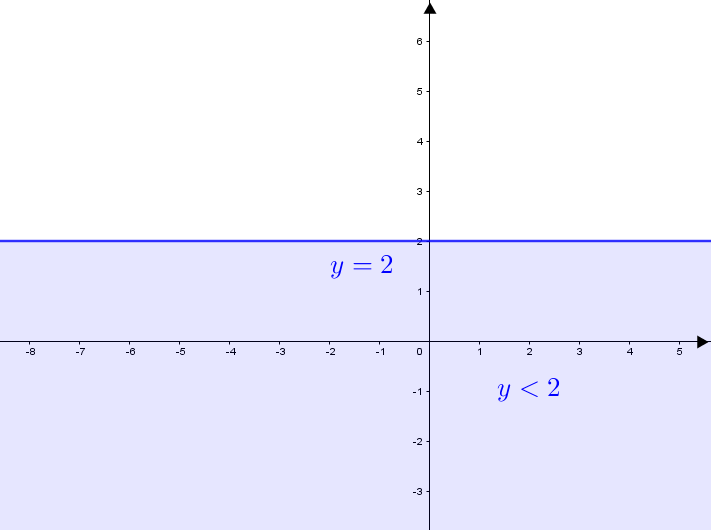
Aqui, para atender à desigualdade [tex]y \leqslant 2\, [/tex], nos interessam os pontos que estão abaixo de [tex]s\, [/tex] ([tex]y \lt 2\, [/tex]) e também os pontos que estão sobre [tex]s\, [/tex] ([tex]y=2\, [/tex]).
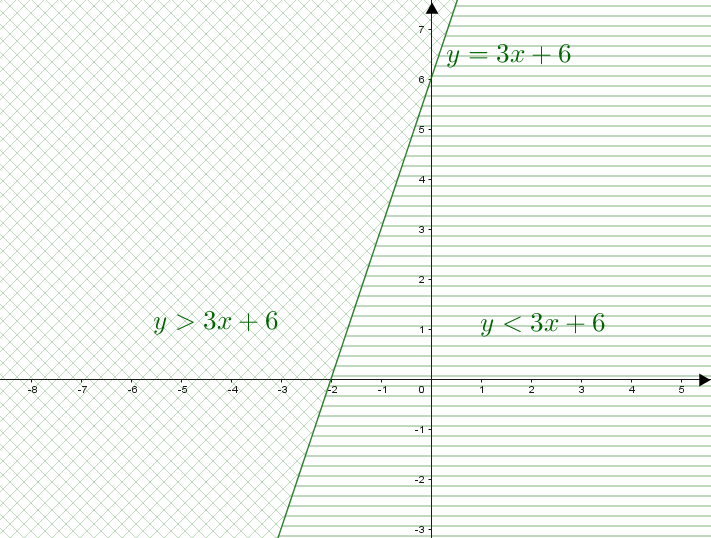
Para atender esta desigualdade [tex]y\lt 3x+6\, [/tex], nos interessam os pontos que estão abaixo de [tex]t\, .[/tex]
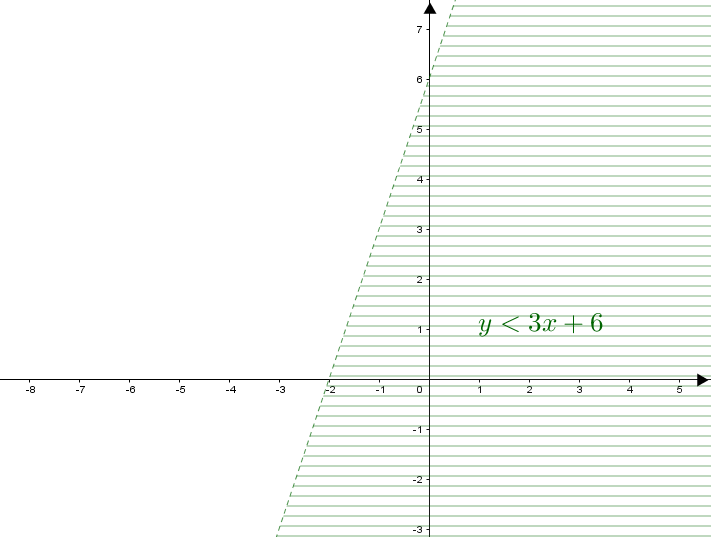
Vamos, agora, observar as três regiões que representam geometricamente as desigualdades que compõem o sistema, para fazermos a interseção delas, já que as três desigualdades devem ser simultaneamente satisfeitas.
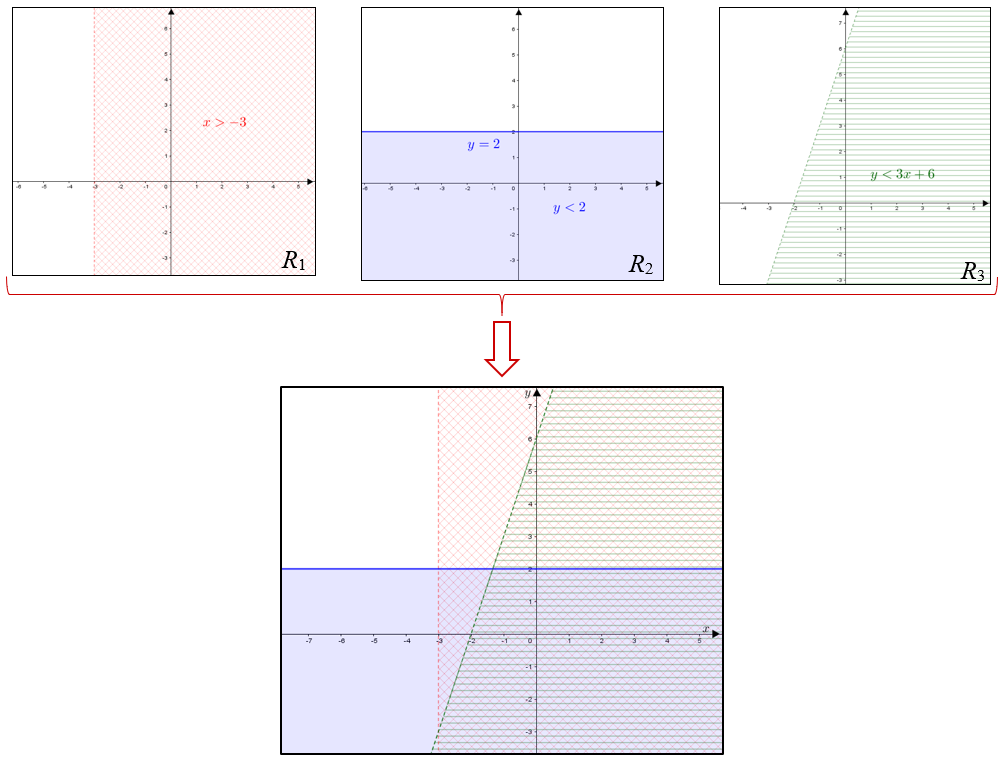
Passando a limpo, a solução da desigualdade proposta no problema é a região destacada na figura abaixo. Observem atentamente as fronteiras da região.
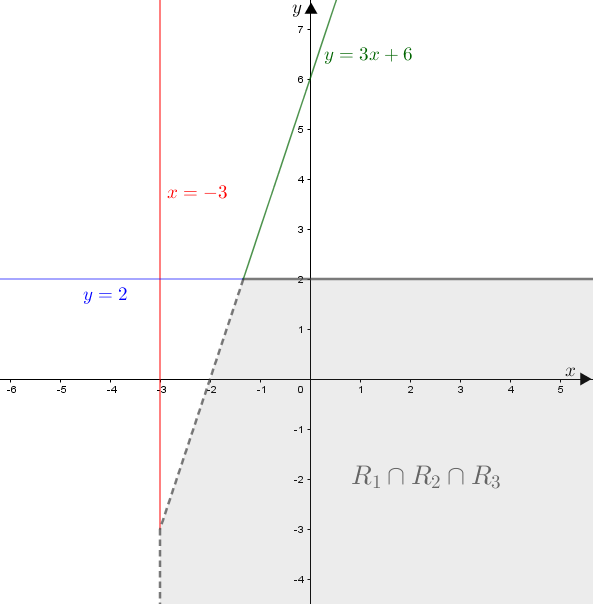
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
