✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Muito Difícil)
Em um triângulo retângulo [tex]ABC[/tex], com ângulo reto no vértice [tex]C[/tex], temos que
[tex]\hspace{3cm}6(cos^3 \hat{A})=\dfrac{sen\hat{A}+sen\hat{B}}{tan\hat{A}+tan\hat{B}}[/tex].
Determine [tex]tan\hat{A}[/tex].

Lembrete
Para solucionar este problema, vamos precisar de algumas das relações entre as medidas dos lados e dos ângulos internos de um triângulo retângulo. Seja, então, um triângulo retângulo [tex]ABC[/tex], cujos lados têm comprimentos [tex]a,\, b,\, c\, [/tex] e os ângulos agudos têm medidas [tex]\alpha[/tex] e [tex]\beta[/tex], conforme indicado na figura.
Então:
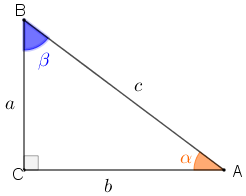
✐ [tex]sen\, \hat{A}=sen\, \alpha=\dfrac{a}{c}=cos\, \beta=cos\, \hat{B}[/tex]
✐ [tex]cos\, \hat{A}=cos\, \alpha=\dfrac{b}{c}=sen\, \beta=sen\, \hat{B}[/tex]
✐ [tex]tan\, \hat{A}=tan\, \alpha=\dfrac{a}{b}[/tex]
✐ [tex]tan\, \hat{B}=tan\, \beta=\dfrac{b}{a}[/tex]
Solução 1
Seja [tex]ABC[/tex] um triângulo retângulo.
A partir da notação indicada na figura do Lembrete, podemos reescrever a igualdade fornecida no problema; observe:
[tex]\qquad 6(cos^3 \hat{A})=\dfrac{sen\hat{A}+sen\hat{B}}{tan\hat{A}+tan\hat{B}}[/tex]
[tex]\qquad 6\left(\dfrac{b}{c}\right)^3=\dfrac{\frac{a}{c}+\frac{b}{c}}{\frac{a}{b}+\frac{b}{a}}[/tex]
[tex]\qquad 6\left(\dfrac{b^3}{c^3}\right)=\dfrac{\frac{a+b}{c}}{\frac{a^2+b^2}{ab}}[/tex]
Pelo Teorema de Pitágoras, [tex]a^2+b^2=c^2[/tex], assim:
[tex]\qquad 6\left(\dfrac{b^3}{c^3}\right)=\dfrac{\frac{a+b}{c}}{\frac{c^2}{ab}}[/tex]
[tex]\qquad 6\left(\dfrac{b^3}{c^3}\right)=\dfrac{ab(a+b)}{c^3}[/tex]
[tex]\qquad 6b^2=a(a+b)[/tex]
[tex]\qquad a^2+ab-6b^2=0.\qquad \textcolor{#800000}{(i)}[/tex]
Essa última igualdade mostra a relação entre os comprimentos [tex]a\, [/tex] e [tex]\, b[/tex] dos catetos de um triângulo retângulo que satisfaz a igualdade indicada no problema.
Como [tex]a\ne 0\, [/tex] e [tex]\, b\ne \, 0[/tex], pois ambos são comprimentos dos catetos de um triângulo, podemos olhar a equação [tex]\textcolor{#800000}{(i)}[/tex] como uma equação do segundo grau na variável [tex]\, a[/tex] ou [tex]b\, [/tex] e se aplicarmos a fórmula de resolução de uma equação do segundo grau podemos escrever [tex]a\, [/tex] em função de [tex]\, b[/tex] ou [tex]b\, [/tex] em função de [tex]\, a[/tex]. Particularmente, vamos considerar [tex]\textcolor{#800000}{(i)}[/tex] como uma equação do segundo grau na variável [tex]\, a[/tex] e dessa forma teremos que:
[tex]\qquad a=\dfrac{-b\pm\sqrt{b^2-(4 \times (-6b^2))}}{2}[/tex]
[tex]\qquad a=\dfrac{-b\pm\sqrt{b^2+24b^2\, }}{2}[/tex]
[tex]\qquad a=\dfrac{-b\pm\sqrt{25b^2\, }}{2}[/tex]
Como sabemos que [tex]b \gt 0\, [/tex], pois é uma medida, temos que:
[tex]\qquad a=\dfrac{-b\pm 5b}{2}[/tex]
[tex]\qquad a=\dfrac{-b+5b}{2} \quad \text{ou} \quad a=\dfrac{-b-5b}{2}[/tex]
[tex]\qquad a=\dfrac{4b}{2} \quad \text{ou} \quad a=\dfrac{-6b}{2}[/tex]
[tex]\qquad a=2b \quad \text{ou} \quad a=-3b[/tex]
Como [tex]a\, [/tex] e [tex]\, b[/tex] são positivos, a igualdade [tex]a=-3b[/tex] não nos interessa. Assim, [tex]a=2b[/tex] e, portanto,
[tex]\qquad \fcolorbox{black}{#eee0e5}{$tan\, \hat{A}=\dfrac{a}{b}=\dfrac{2b}{b}=2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.

Ajuda para a segunda Solução
Para a próxima solução, precisaremos de algumas das relações do Lembrete, mas escritas de maneira diferente.
Considere um triângulo retângulo [tex]ABC[/tex], cujos ângulos agudos têm medidas [tex]\alpha[/tex] e [tex]\beta[/tex], conforme indicado na figura.
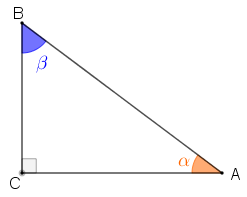
✐ [tex]sen\, \hat{A}=sen\, \alpha=cos\, \beta=cos\, \hat{B}[/tex]
✐ [tex]cos\, \hat{A}=cos\, \alpha=sen\, \beta=sen\, \hat{B}[/tex]
✐ [tex]tan\, \hat{A}=tan\, \alpha=\dfrac{sen\, \alpha}{cos\, \alpha}[/tex]
✐ [tex]tan\, \hat{B}=tan\, \beta=\dfrac{sen\, \beta}{cos\, \beta}[/tex]
Solução 2
Seja [tex]ABC[/tex] um triângulo retângulo.
A partir da notação indicada na figura da Ajuda, podemos reescrever a igualdade fornecida no problema da seguinte maneira:
[tex]\qquad \begin{align*}6(cos^3 \, \hat{A})&=\dfrac{sen\, \hat{A}+sen\, \hat{B}}{tan\, \hat{A}+tan\, \hat{B}}=\dfrac{sen\, \hat{A}+cos\, \hat{A}}{\frac{sen\, \hat{A}}{cos\, \hat{A}}+\frac{sen\, \hat{B}}{cos\, \hat{B}}}\\
&=\dfrac{sen\, \hat{A}+cos\, \hat{A}}{\frac{sen\, \hat{A}}{cos\, \hat{A}}+\frac{cos\, \hat{A}}{sen\, \hat{A}}}=\dfrac{sen\, \hat{A}+cos\, \hat{A}}{\frac{sen^2\hat{A}+cos^2\hat{A}}{cos\, \hat{A}\cdot sen\, \hat{A}}}\\
\end{align*}[/tex]
A relação fundamental da trigonometria nos garante que [tex]sen^2\hat{A}+cos^2\hat{A}=1[/tex], assim:
[tex]\qquad \begin{align*}6(cos^3 \, \hat{A})&=\dfrac{sen\, \hat{A}+cos\, \hat{A}}{\frac{sen^2\hat{A}+cos^2\hat{A}}{cos\, \hat{A}\cdot sen\, \hat{A}}}=\dfrac{sen\, \hat{A}+cos\, \hat{A}}{\frac{1}{cos\, \hat{A}\cdot sen\, \hat{A}}}\\
&=cos\, \hat{A}\cdot sen\, \hat{A}\cdot \left(sen\, \hat{A}+cos\, \hat{A}\right).\\
\end{align*}[/tex]
Como [tex]\hat{A}[/tex] é um ângulo agudo, então [tex]cos\, \hat{A}\ne 0[/tex]; portanto podemos simplificar a última igualdade e, assim:
[tex]\qquad 6(cos^2 \, \hat{A})=sen\, \hat{A}\cdot \left(sen\, \hat{A}+cos\, \hat{A}\right)[/tex]
[tex]\qquad sen\, \hat{A}\left(sen\, \hat{A}+cos\, \hat{A}\right)-6(cos^2 \, \hat{A})=0[/tex]
[tex]\qquad sen\, ^2\hat{A}+sen\, \hat{A}\cdot cos\, \hat{A}-6cos^2 \, \hat{A}=0.[/tex]
Agora, um artifício: [tex]\boxed{sen\, \hat{A}\cdot cos\, \hat{A}}=\boxed{3sen\, \hat{A}\cdot cos\, \hat{A}-2sen\, \hat{A}\cdot cos\, \hat{A}}[/tex], logo:
[tex]\qquad sen\, ^2\hat{A}+\left(sen\, \hat{A}\cdot cos\, \hat{A}\right)-6cos^2 \, \hat{A}=0[/tex]
[tex]\qquad sen\, ^2\hat{A}+\left(3sen\, \hat{A}\cdot cos\, \hat{A}-2sen\, \hat{A}\cdot cos\, \hat{A}\right)-6cos^2 \, \hat{A}=0[/tex]
[tex]\qquad \left(sen\, ^2\hat{A}-2sen\, \hat{A}\cdot cos\, \hat{A}\right)+\left(3sen\, \hat{A}\cdot cos\, \hat{A}-6cos^2 \, \hat{A}\right)=0[/tex]
[tex]\qquad sen\, \hat{A} \left(sen\, \hat{A}-2cos\, \hat{A}\right)+3cos\, \hat{A}\left(sen\, \hat{A}-2cos\, \hat{A}\right)=0[/tex]
[tex]\qquad \left(sen\, \hat{A}+3cos\, \hat{A}\right)\left(sen\, \hat{A}-2cos\, \hat{A}\right)=0.\qquad \textcolor{#800000}{(i)}[/tex]
Sabemos que se um produto é igual a zero, então um dos fatores é zero, não é? Então, segue de [tex] \textcolor{#800000}{(i)}[/tex] que:
► [tex]\qquad \boxed{\left(sen\, \hat{A}+3cos\, \hat{A}\right)=0}\, \, [/tex] ou[tex]\, \, \boxed{\left(sen\, \hat{A}-2cos\, \hat{A}\right)=0}.[/tex]
Mais uma vez observamos que [tex]\hat{A}[/tex] é um ângulo agudo; logo, [tex]cos\, \hat{A}\gt 0[/tex] e [tex]sen\, \hat{A}\gt 0[/tex]. Portanto, [tex]\left(sen\, \hat{A}+3cos\, \hat{A}\right)\gt 0\, [/tex] e com isso necessariamente [tex]\left(sen\, \hat{A}-2cos\, \hat{A}\right)=0.[/tex]
Mas se [tex]sen\, \hat{A}-2cos\, \hat{A}=0\, [/tex] e [tex]\, cos\, \hat{A}\ne 0\, [/tex], segue que:
[tex]\qquad sen\, \hat{A}-2cos\, \hat{A}=0[/tex]
[tex]\qquad sen\, \hat{A}=2cos\, \hat{A}[/tex]
[tex]\qquad \dfrac{sen\, \hat{A}}{cos\, \hat{A}}=2[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$tan\, \hat{A}=2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
