✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 6º ano do E. F. – Nível de dificuldade: Difícil)
Podemos usar o algoritmo da divisão e dividir [tex]870[/tex] por [tex]40[/tex] da seguinte maneira:
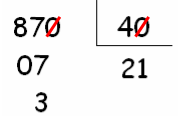
Qual é o quociente e o resto dessa divisão?
Justifique o resultado.

Ajuda
Sejam [tex]n[/tex] e [tex]a[/tex] números naturais, com [tex]a\ne 0.[/tex]
O que acontece com o quociente e o resto da divisão de [tex]n[/tex] por [tex]a[/tex]?
Observemos…
|
[tex]\qquad \qquad \begin{array}{r} n \, \end{array} \begin{array}{|r} \, a \, \, \, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} r \end{array}\begin{array}{r} \, \, \, q \end{array}\qquad \qquad[/tex] |
Ao dividirmos [tex]n[/tex] por [tex]a[/tex] encontraremos um quociente [tex]q [/tex] e um resto [tex]r [/tex], naturais e únicos, tais que: [tex] \, \, \, (1) \, \, 0 \le r \lt a \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, [/tex] [tex](2) \, \, n=q \times a+r[/tex]. |
Solução
A princípio, alguém poderia responder: que pergunta boba; é só olhar para o diagrama da chave que foi apresentado e concluir que o quociente é [tex]21[/tex] e o resto é [tex]3[/tex].
Mas observe que a informação [tex](2) [/tex] da ajuda nos dá uma relação importante entre o dividendo, o divisor, o quociente e o resto de uma divisão euclidiana e com esses valores de quociente e de resto a igualdade [tex](2) [/tex] não é satisfeita:
[tex]\qquad \boxed{21 \times 40+3=843\ne 870} \, .[/tex]
Perceba que no diagrama apresentado, foi feita a divisão de [tex]87[/tex] por [tex]4[/tex], como uma maneira simplificada de efetuarmos a divisão de [tex]870[/tex] por [tex]40[/tex]:
|
[tex]\qquad \qquad \begin{array}{r} 87 \, \end{array} \begin{array}{|r} \, 4 \, \, \, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} \, \, 3 \end{array}\begin{array}{r} \, \, \, 21 \end{array}\qquad \qquad[/tex] |
Os números [tex]q=21 [/tex] e [tex]r=3 [/tex] são, respectivamente, o quociente e o resto da divisão de [tex]87[/tex] por [tex]4[/tex], assim: [tex]\qquad \qquad (3) \, \, 0 \le 3 \lt 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,\, \, \, [/tex] [tex](4) \, \, 87=21 \times 4+3[/tex]. |
Ao multiplicarmos a igualdade [tex](4)[/tex] por [tex]10[/tex], temos que:
[tex]\qquad 87\times 10=\left(21 \times 4+3\right)\times 10[/tex]
[tex]\qquad 870=21 \times 40+30 \, .[/tex]
Assim, como
[tex]\qquad \textcolor{#800000}{(*)} \, \, 0 \le 30 \lt 40 [/tex],
[tex]\qquad \textcolor{#800000}{(**)} \, \, 870=21 \times 40+30[/tex],
a unicidade do resto e do quociente da divisão de [tex]870[/tex] por [tex]40[/tex] nos garante que:
[tex]\qquad \qquad \begin{array}{r}
870 \, \end{array} \begin{array}{|r}
\, 40 \, \, \, \, \\ \hline
\end{array}[/tex]
[tex]\qquad \qquad\begin{array}{r}
\, \, 30
\end{array}\begin{array}{r}
\, \, \, 21
\end{array}[/tex]
ou seja, o resto da divisão de [tex]870[/tex] por [tex]40[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$30$}[/tex] e, o quociente, [tex]\fcolorbox{black}{#eee0e5}{$21$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
