✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Na figura, vemos um quadrado inscrito em uma circunferência que, por sua vez, está inscrita em um outro quadrado.
Cada lado do quadrado externo mede [tex]4 \, cm[/tex].
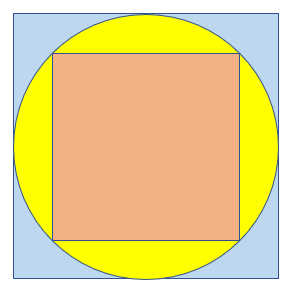
Qual a área em [tex]cm^2[/tex] da região colorida de amarelo?
Solução 1
Observando a figura do problema, vemos que a área da região colorida de amarelo pode ser calculada fazendo a diferença entre a área do círculo e a área do quadrado interno:
[tex]\qquad \qquad \boxed{A_{am}=A_{circ}-A_{qi}}. \qquad \textcolor{#800000}{(i)} [/tex]
Para calcularmos essas duas áreas que definem a área solicitada no problema, precisaremos do raio do círculo e do lado do quadrado interno que aparecem na figura.
Note que, como cada lado do quadrado externo mede [tex]4 \, cm[/tex] e a circunferência que define o círculo está inscrita nesse quadrado, o raio do círculo é [tex]2 \, cm.[/tex] Assim, a área do círculo é:
[tex]\qquad \qquad \boxed{A_{circ}=4\pi \, cm^2}. \qquad \textcolor{#800000}{(ii)} [/tex]
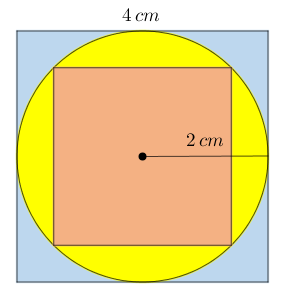
Para calcularmos o comprimento [tex]l[/tex] do lado do quadrado interno, vamos ter um pouquinho mais de trabalho. Perceba, inicialmente, que o interior desse quadrado pode ser decomposto em quatro triângulos retângulos isósceles cujos lados congruentes medem [tex]2 \, cm[/tex], já que estes lados são raios do círculo da figura.
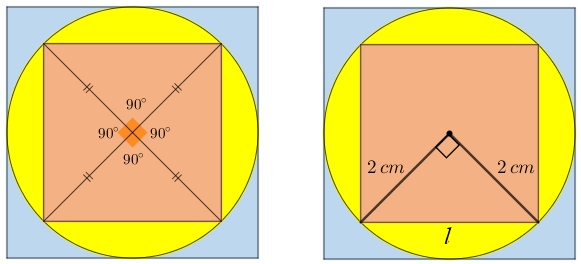
Aplicando o Teorema de Pitágoras a um desses triângulos, obtemos que:
[tex]\qquad l^2=2^2+2^2\\
\qquad l^2=8 \\
\qquad l=\pm \sqrt{8}\\
\qquad l=\pm 2\sqrt{2}[/tex]
[tex] \qquad l=2\sqrt{2} \, cm[/tex], já que [tex] l \gt 0[/tex] por ser um comprimento.
Logo, a área do quadrado interno é:
[tex]\qquad \qquad \boxed{A_{qi}=8 \, cm^2}. \qquad \textcolor{#800000}{(iii)} [/tex]
Finalizando, por [tex]\textcolor{#800000}{(i)} [/tex], [tex]\textcolor{#800000}{(ii)} [/tex] e [tex]\textcolor{#800000}{(iii)} [/tex], segue que:
[tex] \qquad A_{am}=A_{circ}-A_{qi}=\left(4\pi-8\right) \, cm^2.[/tex]
Portanto, a área da região colorida de amarelo é [tex]\fcolorbox{black}{#eee0e5}{$\left(4\pi-8\right) \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
A figura do problema nos sugere que a área da região colorida de amarelo pode ser calculada fazendo a diferença entre a área do círculo e a área do quadrado interno, conforme denotamos a seguir:
[tex]\qquad \qquad A_{am}=A_{circ}-A_{qi}.[/tex]
Assim, se [tex]l[/tex] e [tex]R[/tex] são os comprimentos em centímetros dos lados do quadrado interno e do raio, respectivamente, segue que
[tex]\qquad \qquad \boxed{A_{am} = \pi R^2 – l^2}. \qquad \textcolor{#800000}{(i)} [/tex]
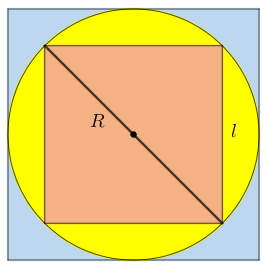
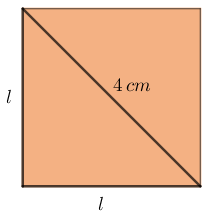
Mas sabemos que o raio da circunferência é [tex]2\,cm[/tex], logo a diagonal do quadrado mede [tex]4\,cm[/tex]; portanto, utilizando o Teorema de Pitágoras, temos que:
[tex]\qquad \qquad l^2 + l^2 = d^2\\
\qquad \qquad 2l^2 = 4^2 \\
\qquad \qquad \boxed{l^2 = 8\ cm^2} \, .[/tex]
Logo, segue de [tex]\textcolor{#800000}{(i)} [/tex] que
[tex] \qquad \qquad A_{am} = \pi \cdot 2^2 – 8 \\
\qquad \qquad A_{am} = 4\pi – 8[/tex]
e, assim, a área da região colorida de amarelo é [tex]\fcolorbox{black}{#eee0e5}{$\left(4\pi-8\right) \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 3
Se o quadrado externo tem 4 cm de cada lado, a circunferência inscrita nele terá 4 cm de diâmetro. Consequentemente, o raio da circunferência terá 2 cm. Usando a fórmula a=π.r² para calcular a área do círculo, temos que:
a=3,14.2²
a=3,14.4
a=12,56
A área da circunferência será aproximadamente 12,56 cm².
Como a diagonal do quadrado inteiro é um diâmetro da circunferência, o comprimento da diagonal do quadrado interno é 4 cm. Dividindo o quadrado interno em 2 partes, a partir da diagonal, teremos 2 triângulos retângulos. Usando o Teorema de Pitágoras:
d²=l²+l²
d²=2l²
l²=d²/2
l²=4²/2
l²=16/2
l²=8
l=√8
l=√2³
l=2√2
Descobrimos então que o lado do quadrado interno é 2√2. Como a área do quadrado é l*l, a área do quadrado será 2√2*2√2=8 cm². Agora basta subtrair esse valor da área do círculo, para saber a área colorida de amarelo: 12,56-8,00=4,56.
Resposta: A área colorida de amarelo na figura será de 4,56 cm², aproximadamente.
Solução elaborada pelo COM OCTETO MATEMÁTICO.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
