.Problema para ajudar na escola: Obtendo quadrados perfeitos

Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)

Um número natural [tex]A[/tex] é dito um quadrado perfeito se existir um número natural [tex]n[/tex] tal que [tex]A=n^2.[/tex] Assim, um quadrado perfeito é simplesmente o produto de um número natural por si próprio: [tex]\boxed{A=n^2=n\cdot n}.[/tex]

Preencha a tabela abaixo utilizando os [tex]16[/tex] primeiros números naturais não nulos, sem repetição, de modo que a soma de dois ”números vizinhos” seja um quadrado perfeito.

Solução

Observe inicialmente que o menor e o maior número resultante da soma de dois números naturais distintos escolhidos dentre os [tex]16[/tex] primeiros números naturais não nulos são [tex]1+2=3[/tex] e [tex]15+16=31[/tex], respectivamente.
Por outro lado, os quadrados perfeitos entre [tex]3[/tex] e [tex]31[/tex] são [tex]4=2^2[/tex], [tex]9=3^2[/tex], [tex]16=4^2[/tex] e [tex]25=5^2[/tex], e esses quatro quadrados perfeitos podem ser escritos como soma de números naturais distintos entre [tex]1[/tex] e [tex]16[/tex] das seguintes formas:

• [tex]4=\textcolor{red}{1}+\textcolor{#FF00FF}{3}[/tex];
• [tex]9=\textcolor{red}{1}+\textcolor{#4CC417}{8}[/tex]; [tex]9=\textcolor{blue}{2}+\textcolor{#FFA62F}{7}[/tex]; [tex]9=\textcolor{#FF00FF}{3}+\textcolor{#A52A2A}{6}[/tex]; [tex]9=\textcolor{#00FFFF}{4}+\textcolor{#00FF00}{5}[/tex];
• [tex]16=\textcolor{red}{1}+\textcolor{#FFB86B}{15}[/tex]; [tex]16=\textcolor{blue}{2}+\textcolor{#60D4FF}{14}[/tex]; [tex]16=\textcolor{#FF00FF}{3}+\textcolor{#934CFF}{13}[/tex]; [tex]16=\textcolor{#00FFFF}{4}+\textcolor{#D98BFF}{12}[/tex]; [tex]16=\textcolor{#00FF00}{5}+\textcolor{#43BFC7}{11}[/tex]; [tex]16=\textcolor{#A52A2A}{6}+\textcolor{#F535AA}{10}[/tex]; [tex]16=\textcolor{#FFA62F}{7}+\textcolor{#800080}{9}[/tex];
• [tex]25=\textcolor{#800080}{9}+\textcolor{# 008000}{16}[/tex]; [tex]25=\textcolor{#F535AA}{10}+\textcolor{#FFB86B}{15}[/tex]; [tex]25=\textcolor{#43BFC7}{11}+\textcolor{#60D4FF}{14}[/tex]; [tex]25=\textcolor{#D98BFF}{12}+\textcolor{#934CFF}{13}[/tex].

Para melhor visualização dos vizinhos possíveis para cada número, vamos construir uma tabela com todas as combinações possíveis.

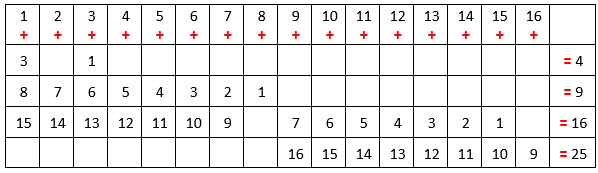
Note que os números [tex]8[/tex] e [tex]16[/tex] só podem ter um vizinho, já que são parcelas de apenas uma soma cada um; esses vizinhos são [tex]1[/tex] e [tex]9[/tex], respectivamente. Dessa forma, [tex]8[/tex] e [tex]16[/tex] ficarão nos extremos da tabela.

\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#4CC417}{8}&\textcolor{red}{1}&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\textcolor{#800080}{9}&\textcolor{#008000}{16}\\
\hline \end{array}

\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#008000}{16}&\textcolor{#800080}{9}&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\textcolor{red}{1}&\textcolor{#4CC417}{8}\\
\hline
\end{array}
Veja que o [tex]1[/tex] e o [tex]3[/tex] têm três possíveis vizinhos, mas os números restantes têm apenas dois possíveis vizinhos. Particularmente, o segundo vizinho do [tex]9[/tex] é o [tex]7[/tex] e com isso completamos mais um espaço das duas possíveis tabelas.

[tex]\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#4CC417}{8}&\textcolor{red}{1}&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\textcolor{#FFA62F}{7}&\textcolor{#800080}{9}&\textcolor{#008000}{16}\\
\hline
\end{array}\\
\,\\
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#008000}{16}&\textcolor{#800080}{9}&\textcolor{#FFA62F}{7}&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\,\,&\textcolor{red}{1}&\textcolor{#4CC417}{8}\\
\hline
\end{array}[/tex]

O segundo vizinho do [tex]7[/tex] é o [tex]2[/tex]. O segundo vizinho do [tex]2[/tex] é o [tex]14[/tex]. O segundo vizinho do [tex]14[/tex] é o [tex]11[/tex]. O segundo vizinho do [tex]11[/tex] é o [tex]5[/tex]. O segundo vizinho do [tex]5[/tex] é o [tex]4[/tex]. O segundo vizinho do [tex]4[/tex] é o [tex]12[/tex]. O segundo vizinho do [tex]12[/tex] é o [tex]13[/tex]. O segundo vizinho do [tex]13[/tex] é o [tex]3[/tex]. Paramos por aqui, por enquanto.
Vejam nossas duas tabelas:

[tex]\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#4CC417}{8}&\textcolor{red}{1}&\,\,&\,\,&\,\,&\textcolor{#FF00FF}{3}&\textcolor{#934CFF}{13}&\textcolor{#D98BFF}{12}&\textcolor{#00FFFF}{4}&\textcolor{#00FF00}{5}&\textcolor{#43BFC7}{11}&\textcolor{#60D4FF}{14}&\textcolor{blue}{2}&\textcolor{#FFA62F}{7}&\textcolor{#800080}{9}&\textcolor{#008000}{16}\\
\hline
\end{array}\\
\,\\
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#008000}{16}&\textcolor{#800080}{9}&\textcolor{#FFA62F}{7}&\textcolor{blue}{2}&\textcolor{#60D4FF}{14}&\textcolor{#43BFC7}{11}&\textcolor{#00FF00}{5}&\textcolor{#00FFFF}{4}&\textcolor{#D98BFF}{12}&\textcolor{#934CFF}{13}&\textcolor{#FF00FF}{3}&\,\,&\,\,&\,\,&\textcolor{red}{1}&\textcolor{#4CC417}{8}\\
\hline
\end{array}.[/tex]

Os possíveis vizinhos do [tex]3[/tex] seriam [tex]1[/tex], [tex]6[/tex] e [tex]13[/tex]; mas, como [tex]1[/tex] e [tex]13[/tex] já foram utilizados, resta apenas o [tex]6.[/tex]

[tex]
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#4CC417}{8}&\textcolor{red}{1}&\,\,&\,\,&\textcolor{#A52A2A}{6}&\textcolor{#FF00FF}{3}&\textcolor{#934CFF}{13}&\textcolor{#D98BFF}{12}&\textcolor{#00FFFF}{4}&\textcolor{#00FF00}{5}&\textcolor{#43BFC7}{11}&\textcolor{#60D4FF}{14}&\textcolor{blue}{2}&\textcolor{#FFA62F}{7}&\textcolor{#800080}{9}&\textcolor{#008000}{16}\\
\hline
\end{array}\\
\,\\
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#008000}{16}&\textcolor{#800080}{9}&\textcolor{#FFA62F}{7}&\textcolor{blue}{2}&\textcolor{#60D4FF}{14}&\textcolor{#43BFC7}{11}&\textcolor{#00FF00}{5}&\textcolor{#00FFFF}{4}&\textcolor{#D98BFF}{12}&\textcolor{#934CFF}{13}&\textcolor{#FF00FF}{3}&\textcolor{#A52A2A}{6}&\,\,&\,\,&\textcolor{red}{1}&\textcolor{#4CC417}{8}\\
\hline
\end{array}[/tex]

Dos possíveis vizinhos do [tex]1[/tex] resta apenas o [tex]15.[/tex]

[tex]
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#4CC417}{8}&\textcolor{red}{1}&\textcolor{#FFB86B}{15}&\,\,\,&\textcolor{#A52A2A}{6}&\textcolor{#FF00FF}{3}&\textcolor{#934CFF}{13}&\textcolor{#D98BFF}{12}&\textcolor{#00FFFF}{4}&\textcolor{#00FF00}{5}&\textcolor{#43BFC7}{11}&\textcolor{#60D4FF}{14}&\textcolor{blue}{2}&\textcolor{#FFA62F}{7}&\textcolor{#800080}{9}&\textcolor{#008000}{16}\\
\hline
\end{array}\\
\,\\
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#008000}{16}&\textcolor{#800080}{9}&\textcolor{#FFA62F}{7}&\textcolor{blue}{2}&\textcolor{#60D4FF}{14}&\textcolor{#43BFC7}{11}&\textcolor{#00FF00}{5}&\textcolor{#00FFFF}{4}&\textcolor{#D98BFF}{12}&\textcolor{#934CFF}{13}&\textcolor{#FF00FF}{3}&\textcolor{#A52A2A}{6}&\,\,\,&\textcolor{#FFB86B}{15}&\textcolor{red}{1}&\textcolor{#4CC417}{8}\\
\hline
\end{array}[/tex]

Finalizando e conferindo, o número [tex]10[/tex], que sobrou, é de fato um possível vizinho do [tex]6[/tex] e do [tex]15.[/tex] Portanto, são estas as possíveis tabelas que atendem às hipóteses do problema:

[tex]\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#4CC417}{8}&\textcolor{red}{1}&\textcolor{#FFB86B}{15}&\textcolor{#F535AA}{10}&\textcolor{#A52A2A}{6}&\textcolor{#FF00FF}{3}&\textcolor{#934CFF}{13}&\textcolor{#D98BFF}{12}&\textcolor{#00FFFF}{4}&\textcolor{#00FF00}{5}&\textcolor{#43BFC7}{11}&\textcolor{#60D4FF}{14}&\textcolor{blue}{2}&\textcolor{#FFA62F}{7}&\textcolor{#800080}{9}&\textcolor{#008000}{16}\\
\hline
\end{array}\\
\,\\
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textcolor{#008000}{16}&\textcolor{#800080}{9}&\textcolor{#FFA62F}{7}&\textcolor{blue}{2}&\textcolor{#60D4FF}{14}&\textcolor{#43BFC7}{11}&\textcolor{#00FF00}{5}&\textcolor{#00FFFF}{4}&\textcolor{#D98BFF}{12}&\textcolor{#934CFF}{13}&\textcolor{#FF00FF}{3}&\textcolor{#A52A2A}{6}&\textcolor{#F535AA}{10}&\textcolor{#FFB86B}{15}&\textcolor{red}{1}&\textcolor{#4CC417}{8}\\
\hline
\end{array}.[/tex]

Solução elaborada pelos Moderadores do Blog.