✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
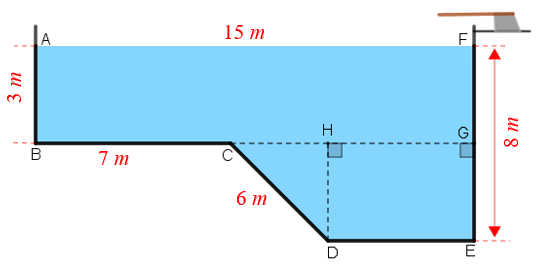
A largura de uma piscina cuja vista lateral é mostrada na figura abaixo é [tex]10 \, m[/tex].
Determine o seu volume aproximado.

Lembrete e notação
Não importa se um prisma é regular ou não, se ele é um prisma reto ou oblíquo: o seu volume [tex]V[/tex] é dado pelo produto entre a área da sua base e a sua altura: [tex]\boxed{V=\text{área da base} \times \text{altura}} \, .[/tex]
Abaixo vemos os volumes de dois prismas que utilizaremos: o prisma trapezoidal e o prisma retangular (paralelepípedo).
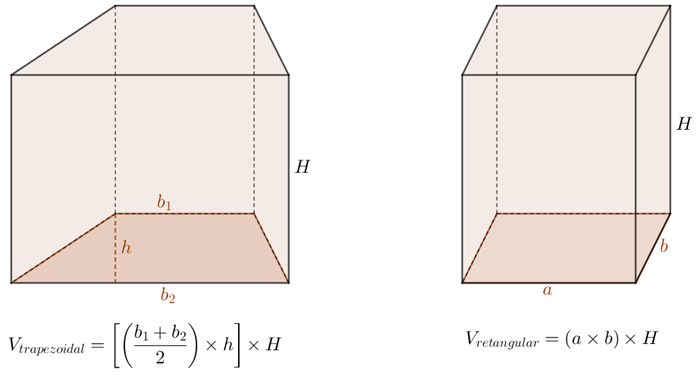
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]P[/tex] e [tex]Q[/tex], por [tex]\overline{PQ}[/tex] e o seu comprimento por [tex]PQ[/tex].
Solução
Inicialmente, vamos observar o triângulo [tex]CDH[/tex] que aparece na vista lateral da piscina.
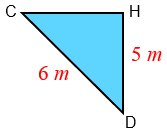
- Como a hipotenusa desse triângulo mede [tex]6 \, m[/tex], e o cateto [tex]\overline{HD} \, \, 8-3=5 \, m[/tex], o Teorema de Pitágoras
- Para o cálculo do volume, observe que a piscina tem a forma de um sólido que pode ser decomposto em dois prismas: um retangular e um trapezoidal.
- Se [tex]V_r[/tex] é o volume do prisma retangular, então,
de acordo com o Lembrete: - Se [tex]V_t[/tex] é o volume do prisma trapezoidal, então,
de acordo com o Lembrete:
nos garante que:
[tex]\qquad 6^2=5^2+CH^2[/tex]
[tex]\qquad 36=25+CH^2[/tex]
[tex]\qquad CH=\pm\sqrt{11}[/tex]
[tex]\qquad CH = \sqrt{11}[/tex], já que [tex]CH\gt 0.[/tex]
Com isso, obtemos também a medida do segmento [tex]\overline{DE}: 15-7-\sqrt{11}=8-\sqrt{11} \, m.[/tex]
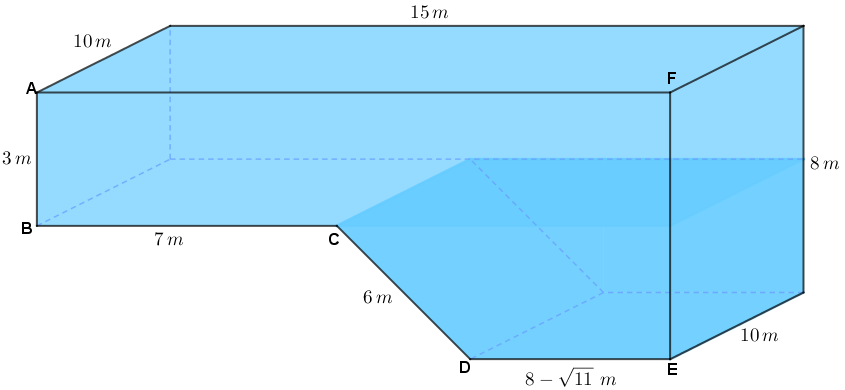
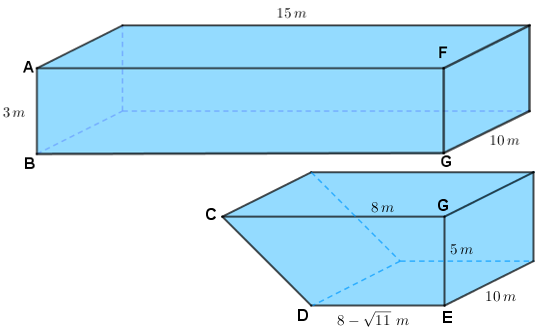
As medidas necessárias para os cálculos estão na figura ao lado.
[tex]V_r=\left(15 \times 3\right) \times 10[/tex]
[tex]\boxed{V_r=450 \, m^3} \, .[/tex]
[tex]V_t=\left [ \left (\frac{(8-\sqrt{11})+8}{2} \right) \times 5 \right ] \times 10[/tex]
[tex]V_t=\left [ (16-\sqrt{11}) \times 5 \right ] \times 5[/tex]
[tex]\boxed{V_t= 400-25\sqrt{11} m^3} \, .[/tex]
Como o volume [tex]V[/tex] da piscina é a soma dos volumes dos dois prismas, segue que:
[tex]\qquad V= V_r+V_t[/tex]
[tex]\qquad V= 450+400-25\sqrt{11}[/tex]
[tex]\qquad V= 850-25\sqrt{11} \, m^3[/tex]
[tex]\qquad\boxed{ V\approx 767 \, m^3} \, .[/tex]
Sabemos que [tex]1 \, litro=0,001 \, m^3 \, [/tex]; assim, [tex]1000 \, litros=1 \, m^3 \, [/tex] e consequentemente [tex]767 \, m^3=767000 \, litros.[/tex] Portanto, o volume da piscina em questão é de aproximadamente [tex] \, \fcolorbox{black}{#eee0e5}{$ 767.000 \, litros$} \, .[/tex]
Muita água, hem?
A água é um bem precioso;
não se esqueçam de economizar, pessoal!
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
