✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
Considere a seguinte sequência numérica: [tex]26\;;\; 2006 \;; \;202606\; ;\; 20200606 \;;\; \dots [/tex]
O primeiro número dessa sequência é o [tex]26[/tex] e, a partir daí, os próximos termos são definidos introduzindo-se, alternadamente,
- [tex]00[/tex] entre os algarismos centrais [tex]2[/tex] e [tex]6[/tex]
- [tex]26[/tex] entre os algarismos centrais [tex]0[/tex] e [tex]0[/tex].
e
Reveja os primeiros termos da sequência:
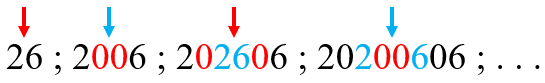
Calcule a soma de todos os algarismos do [tex]2020^\circ[/tex] número dessa sequência.
Adaptado da IX Olimpíada Regional de Matemática Santa Catarina, 2006.
Solução
Para resolver este problema, precisamos analisar o padrão dos termos da sequência definida e o padrão das somas dos algarismos desses termos.
Vejamos:
- O primeiro termo é o [tex]26[/tex] e a soma de seus algarismos é [tex]8[/tex].
- O segundo termo é o [tex]2\textcolor{red}{00}6[/tex] e a soma de seus algarismos é também [tex]8[/tex].
- O terceiro termo é o [tex]2\textcolor{red}{0}\textcolor{#3BB9FF}{26}\textcolor{red}{0}6[/tex] e a soma de seus algarismos é [tex]8+\textcolor{#3BB9FF}{(2+6)}=16=2\times 8[/tex].
- O quarto termo é o [tex]20\textcolor{#3BB9FF}{2}\textcolor{red}{00}\textcolor{#3BB9FF}{6}06[/tex] e a soma de seus algarismos é também [tex]16[/tex].
- O quinto termo é o [tex]202\textcolor{red}{0}\textcolor{#3BB9FF}{26}\textcolor{red}{0}606[/tex] e a soma de seus algarismos é [tex]16+\textcolor{#3BB9FF}{(2+6)}=24=3\times 8[/tex].
- O sexto termo é o [tex]2020\textcolor{#3BB9FF}{2}\textcolor{red}{00}\textcolor{#3BB9FF}{6}0606[/tex] e a soma de seus algarismos é também [tex]24[/tex].
- O sétimo termo é o [tex]20202\textcolor{red}{0}\textcolor{#3BB9FF}{26}\textcolor{red}{0}60606[/tex] e a soma de seus algarismos é [tex]24+\textcolor{#3BB9FF}{(2+6)}=32=4\times 8[/tex].
- O oitavo termo é o [tex]202020\textcolor{#3BB9FF}{2}\textcolor{red}{00}\textcolor{#3BB9FF}{6}060606[/tex] e a soma de seus algarismos é também [tex]32[/tex].
Uma tabela talvez possa ajudar na visualização dos padrões:
[tex]\begin{array}{c|c|c}
& \text{Termos}&\text{Soma dos algarismos}\\
\hline
1^\circ \text{ termo}&26 & 1\times 8\\
\hline
2^\circ \text{ termo}&2\textcolor{red}{00}6 & 1 \times 8\\
\hline
3^\circ \text{ termo}&20\textcolor{#3BB9FF}{26}06 & 2\times 8\\
\hline
4^\circ \text{ termo}&202\textcolor{red}{00}606 & 2\times 8\\
\hline
5^\circ \text{ termo}&2020\textcolor{#3BB9FF}{26}0606 & 3\times 8\\
\hline
6^\circ \text{ termo}&20202\textcolor{red}{00}60606 & 3\times 8\\
\hline
7^\circ \text{ termo}&202020\textcolor{#3BB9FF}{26}060606 & 4\times 8\\
\hline
8^\circ \text{ termo}&2020202\textcolor{red}{00}6060606 & 4\times 8\\
\hline
\vdots&\vdots&\vdots
\end{array}[/tex]
Perceba que:
- Os termos de ordem par são formados a partir de seus respectivos antecessores imediatos de ordem ímpar, acrescentando os algarismos [tex]\textcolor{red}{00}[/tex]. Assim, a soma dos algarismos de cada termo de ordem par é a mesma soma dos algarismos do termo de ordem ímpar que o precede imediatamente.
- A partir do terceiro termo, os termos de ordem ímpar são formados a partir de seus respectivos antecessores imediatos de ordem par, acrescentando-se os algarismos [tex]\textcolor{#3BB9FF}{26}[/tex].
Logo, a soma dos algarismos de cada termo de ordem ímpar, a partir do terceiro termo, é a soma dos algarismos do termo de ordem par que o antecede imediatamente, acrescida de [tex]2+6=8[/tex].
Dessa forma, se denotarmos por
[tex]\qquad \left(a_n\right)=\left(26,2006,202606,20200606,2020260606,\cdots\right)[/tex]
a sequência original, e por
[tex]\qquad \left(s_n\right)=\left(8,8,16,16,24,24,32,32,\cdots\right)[/tex]
a sequência formada pela soma dos algarismos dos respectivos termos de [tex]\left(a_n\right)[/tex], podemos verificar que:
[tex]\qquad s_{2n}=s_{2n-1}=8n[/tex], para todo [tex]n \in \{1,2,3,4,\cdots\}[/tex].
Veja alguns exemplos:
- Para [tex]n=1[/tex], [tex]\boxed{s_{2}=s_{1}=8}[/tex].
- Para [tex]n=2[/tex], [tex]\boxed{s_{4}=s_{3}=16}[/tex].
- Para [tex]n=3[/tex], [tex]\boxed{s_{6}=s_{5}=24}[/tex].
- Para [tex]n=4[/tex], [tex]\boxed{s_{8}=s_{7}=32}[/tex].
- Para [tex]n=5[/tex], [tex]\boxed{s_{10}=s_{9}=40}[/tex].
Com isso, temos que:
[tex]\qquad s_{2020}=s_{2 \times 1010}=s_{2 \times 1010-1}=8 \times 1010=8080[/tex]
e, portanto, a soma de todos os algarismos do [tex]2020^\circ[/tex] número da sequência definida no problema é [tex] \fcolorbox{black}{#eee0e5}{$8080$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
