✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
No conjunto [tex]A[/tex] dos números naturais de [tex]1[/tex] a [tex]1000[/tex], [tex]A=\{1, 2, 3, … , 1000\}[/tex], quantos múltiplos simultâneos de [tex]6[/tex] e [tex]9[/tex] existem?
Solução
Vamos denotar, respectivamente, por [tex]S[/tex] e por [tex]H[/tex] o conjunto dos múltiplos positivos de [tex]6[/tex] e de [tex]9[/tex] que estejam no conjunto [tex]A[/tex]. Observe que:
- existem elementos de [tex]S[/tex] que não estão em [tex]H[/tex]; como o próprio [tex]6[/tex], por exemplo;
- existem elementos de [tex]H[/tex] que não estão em [tex]S[/tex]; como por exemplo o próprio [tex]9[/tex];
- mas também existem elementos que estão em [tex]S[/tex] e em [tex]H[/tex]; como o [tex]18[/tex], já que [tex]18=3 \times 6[/tex] e [tex]18=2 \times 9[/tex];
- existem elementos de [tex]A[/tex] que não estão em [tex]H[/tex] e nem em [tex]S[/tex]; como [tex]1[/tex];
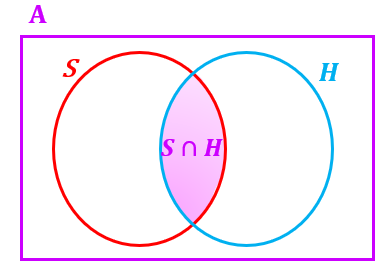
assim podemos representar os três conjuntos [tex]A[/tex], [tex]S[/tex] e [tex]H[/tex] como indicado na figura a seguir.
O que precisamos determinar é quantos elementos do conjunto [tex]A[/tex] são elementos simultaneamente dos conjuntos [tex]S[/tex] e [tex]H[/tex], ou seja, o número de elementos do conjunto usualmente denominado de "interseção de [tex]S[/tex] e [tex]H[/tex]" e denotado por [tex]S\cap H[/tex].
Os múltiplos simultâneos de [tex]6[/tex] e [tex]9[/tex] são os múltiplos do mínimo múltiplo comum de [tex]6[/tex] e [tex]9[/tex], [tex]mmc(6,9)[/tex]; e, como [tex]6=2\times 3[/tex] e [tex]9=3^2[/tex], então [tex]mmc(6,9)=2\times 3^2=18.[/tex]
Estamos interessados, portanto, na quantidade de números que satisfaçam duas condições:
[tex]\textcolor{#800000}{(i)}[/tex] sejam múltiplos de [tex]18[/tex];
[tex]\textcolor{#800000}{(ii)}[/tex] estejam no conjunto [tex]A[/tex].
Seja [tex]x[/tex] um desses números.
Por [tex]\textcolor{#800000}{(i)}[/tex], [tex]x[/tex] é múltiplo de [tex]18[/tex]; logo, existe um número natural [tex]t[/tex] tal que [tex]x=18t[/tex].
Por [tex]\textcolor{#800000}{(ii)}[/tex], [tex]x \in A[/tex], ou seja, [tex]0\lt x \leqslant 1000[/tex].
Assim, utilizando essas duas informações, segue que:
[tex]\qquad 0\lt x \leqslant 1000[/tex]
[tex]\qquad 0\lt 18t \leqslant 1000[/tex]
[tex]\qquad 0\lt t \leqslant \dfrac{1000}{18}\approx 55,56[/tex].
Mas [tex]t[/tex] é um número natural; logo, [tex]0\lt t \leqslant 55[/tex], ou ainda, [tex]\boxed{1\leqslant t \leqslant 55}\,.[/tex]
Como cada número natural [tex]t[/tex] define um número [tex]x[/tex] que satisfaz as condições do problema, temos [tex] \, \fcolorbox{black}{#eee0e5}{$ 55\,$}[/tex] múltiplos simultâneos de [tex]6[/tex] e [tex]9[/tex] no conjunto [tex]A[/tex].
Aproveitando a notação definida:
[tex]\qquad S\cap N= \{\boxed{\,18t\,} \text{ tal que } 1\leqslant t \leqslant 55 \text{, com }t \in \mathbb{N} \} [/tex];
[tex]\qquad S\cap N= \{\boxed{18\times 1},\boxed{18\times 2},\boxed{18\times 3},\cdots,\boxed{18\times 55} \}[/tex];
[tex]\qquad S\cap N= \{\, \underbrace{18\,,\,36\,,\,54\,,\cdots\,,\,990}_{\text{55 elementos}}\, \}[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
