✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
Quantos múltiplos de [tex]2[/tex] e quantos múltiplos de [tex]3[/tex], que não sejam simultaneamente múltiplos de ambos, existem entre [tex]1[/tex] e [tex]2017[/tex]?
Solução 1
Faremos três observações iniciais.
(1) Os múltiplos naturais de [tex]2[/tex] são da forma [tex]2k[/tex], com [tex]k[/tex] um número natural. Assim:
- como procuramos números naturais da forma [tex]2k[/tex] entre [tex]1[/tex] e [tex]2017 \, [/tex],
- como [tex]1[/tex] e [tex]2017[/tex] são números ímpares,
então, [tex]1\lt 2k \lt 2017[/tex], ou mais precisamente, [tex]2\leqslant 2k \leqslant 2016.[/tex]
Com isso, percebemos que [tex]k[/tex] é um número natural tal que [tex]1\leqslant k \leqslant 1008[/tex] e, portanto, temos [tex]1008[/tex] possíveis valores de [tex]k.[/tex] Consequentemente, existem [tex]\boxed{1008}[/tex] números pares entre [tex]1[/tex] e [tex]2017[/tex].
(2) Os múltiplos naturais de [tex]3[/tex] são da forma [tex]3t[/tex], com [tex]t[/tex] um número natural. Assim:
- como procuramos números naturais da forma [tex]3t[/tex] entre [tex]1[/tex] e [tex]2017 \, [/tex],
- como sabemos que [tex]1, \, 2[/tex] e [tex]2017[/tex] não são múltiplos de [tex]3[/tex],
então, [tex]2\lt 3t \lt 2017[/tex], ou mais precisamente, [tex]3\leqslant 3t \leqslant 2016.[/tex]
Com isso percebemos que [tex]t[/tex] é um número natural tal que [tex]1\leqslant t \leqslant 672[/tex] e, portanto, temos [tex]672[/tex] possíveis valores de [tex]t.[/tex] Consequentemente, existem [tex]\boxed{672}[/tex] múltiplos de [tex]3[/tex] entre [tex]1[/tex] e [tex]2017[/tex].
(3) Os múltiplos comuns de [tex]2[/tex] e de [tex]3[/tex] são da forma [tex]6n[/tex], com [tex]n[/tex] um número natural. Assim:
- como procuramos números naturais da forma [tex]6n[/tex] entre [tex]1[/tex] e [tex]2017 \, [/tex],
- como [tex]1, \, 2, \, 3, \, 4, \, 5[/tex] e [tex]2017[/tex] não são múltiplos de [tex]6[/tex],
então, [tex]5\lt 6n \lt 2017[/tex], ou mais precisamente, [tex]6\leqslant 6n \leqslant 2016.[/tex]
Com isso percebemos que [tex]n[/tex] é um número natural tal que [tex]1\leqslant n \leqslant 336[/tex] e, portanto, temos [tex]336[/tex] possíveis valores de [tex]n.[/tex] Consequentemente, existem [tex]\boxed{336}[/tex] múltiplos simultâneos de [tex]2[/tex] e de [tex]3[/tex] entre [tex]1[/tex] e [tex]2017[/tex].
Observe agora que:
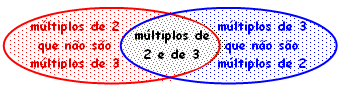
- Dentre os [tex]1008[/tex] múltiplos de [tex]2[/tex] estão incluídos os [tex]336[/tex] múltiplos de [tex]6[/tex] que não nos interessam, pois são múltiplos de [tex]3[/tex] também. Portanto, temos [tex]1008-336=\fcolorbox{black}{#eee0e5}{$672$} \, [/tex] múltiplos de [tex]2[/tex] que não são múltiplos de [tex]3 \, .[/tex]
- Dentre os [tex]672[/tex] múltiplos de [tex]3[/tex] estão incluídos os [tex]336[/tex] múltiplos de [tex]6[/tex] que, também, não nos interessam, pois são múltiplos de [tex]2[/tex]. Portanto temos [tex]672-336=\fcolorbox{black}{#eee0e5}{$336$} \, [/tex] múltiplos de [tex]3[/tex] que não são múltiplos de [tex]2 \, .[/tex]
Dessa forma, existem [tex]\fcolorbox{black}{#eee0e5}{$672+336=1008$} \, [/tex] múltiplos de [tex]2[/tex] e múltiplos de [tex]3[/tex], que não são simultaneamente múltiplos de ambos.
Solução elaborada pelos Moderadores do Blog.
Solução 2
- Observe que entre dois naturais consecutivos existe exatamente um que é múltiplo de [tex]2[/tex]. Assim, podemos procurar os múltiplos de [tex]2[/tex] entre [tex]1[/tex] e [tex]2017[/tex] agrupando todos os números de [tex]1[/tex] a [tex]2017[/tex] de dois em dois.
|
[tex]\qquad \begin{array}{r} 2017\end{array} \begin{array}{|r} \, 2 \, \, \\ \hline \end{array}[/tex] [tex]\qquad\begin{array}{r} \, \, \, 1 \end{array}\begin{array}{r} \, \, \, 1008 \end{array}[/tex] |
Ao dividirmos [tex]2017[/tex] por [tex]2[/tex], obtemos [tex]1008[/tex], com resto [tex]1[/tex]. Isso significa que conseguimos formar [tex]1008[/tex] grupos de dois números consecutivos e o número [tex]2017[/tex] fica sozinho. Pelas nossas observações, teremos então [tex]\boxed{1008}[/tex] múltiplos de [tex]2[/tex] entre [tex]1[/tex] e [tex]2017[/tex]. |
- Observe, agora, que entre três naturais consecutivos existe exatamente um que é múltiplo de [tex]3[/tex]. Logo, para procurar os múltiplos de [tex]3[/tex] entre [tex]1[/tex] e [tex]2017[/tex], vamos agrupar os números de [tex]1[/tex] a [tex]2017[/tex] de três em três.
|
[tex]\qquad \begin{array}{r} 2017\end{array} \begin{array}{|r} \, 3 \, \, \\ \hline \end{array}[/tex] [tex]\qquad\begin{array}{r} \, \, \, 1 \end{array}\begin{array}{r} \, \, \, 672 \end{array}[/tex] |
Ao dividirmos [tex]2017[/tex] por [tex]3[/tex], obtemos [tex]672[/tex], com resto [tex]1[/tex]. Assim, conseguimos formar [tex]672[/tex] grupos de três números consecutivos e o número [tex]2017[/tex] fica sozinho. Pelas nossas observações, teremos então [tex]\boxed{672}[/tex] múltiplos de [tex]3[/tex] entre [tex]1[/tex] e [tex]2017[/tex]. |
- Observe, por último, que entre seis naturais consecutivos existe exatamente um que é múltiplo de [tex]6[/tex], portanto múltiplo de [tex]2[/tex] e de [tex]3[/tex], simultaneamente. Perceba, então, que podemos procurar os múltiplos de [tex]6[/tex] entre [tex]1[/tex] e [tex]2017[/tex], agrupando os números de [tex]1[/tex] a [tex]2017[/tex] de seis em seis.
|
[tex]\qquad \begin{array}{r} 2017\end{array} \begin{array}{|r} \, 6 \, \, \\ \hline \end{array}[/tex] [tex]\qquad\begin{array}{r} \, \, \, 1 \end{array}\begin{array}{r} \, \, \, 336 \end{array}[/tex] |
Ao dividirmos [tex]2017[/tex] por [tex]6[/tex], obtemos [tex]336[/tex], com resto [tex]1[/tex]. Assim, conseguimos formar [tex]336[/tex] grupos de seis números consecutivos e [tex]2017[/tex] fica sozinho. Pelas nossas observações, teremos então [tex]\boxed{336}[/tex] múltiplos de [tex]6[/tex] entre [tex]1[/tex] e [tex]2017[/tex]. |
Para finalizar, observe que:
- Dentre os [tex]1008[/tex] múltiplos de [tex]2[/tex] estão incluídos os [tex]336[/tex] múltiplos de [tex]6[/tex] que não nos interessam, pois são múltiplos de [tex]3[/tex] também. Portanto temos [tex]1008-336=\fcolorbox{black}{#eee0e5}{$672$} \, [/tex] múltiplos de [tex]2[/tex] que não são múltiplos de [tex]3 \, .[/tex]
- Dentre os [tex]672[/tex] múltiplos de [tex]3[/tex] estão incluídos os [tex]336[/tex] múltiplos de [tex]6[/tex] que, também, não nos interessam, pois são múltiplos de [tex]2[/tex]. Portanto temos [tex]672-336=\fcolorbox{black}{#eee0e5}{$336$} \, [/tex] múltiplos de [tex]3[/tex] que não são múltiplos de [tex]2 \, .[/tex]
Pelos nossos cálculos e nossas observações, temos [tex]\fcolorbox{black}{#eee0e5}{$672+336=1008$} \, [/tex] múltiplos de [tex]2[/tex] e múltiplos de [tex]3[/tex], que não são simultaneamente múltiplos de ambos.

Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
