✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M.- Nível de dificuldade: Médio)
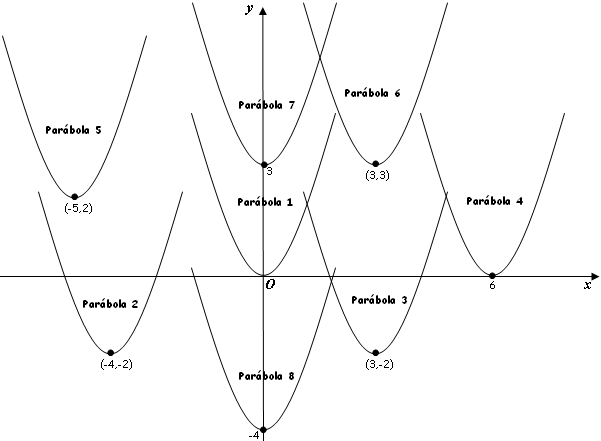
Determine as equações das parábolas esboçadas na figura a seguir, a partir de um plano cartesiano [tex]xOy[/tex], sabendo-se que elas são translações da Parábola 1, cuja equação é [tex]y=x^2[/tex], e que os pontos destacados são os respectivos vértices.

Lembretes
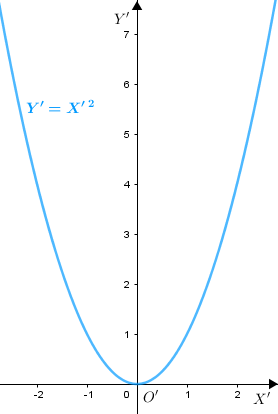
[tex]{\color{#800000}(1)}[/tex] No plano cartesiano [tex]X’O’Y'[/tex], a equação [tex]Y’= X’\,^2[/tex] define uma parábola, com concavidade voltada para cima, cujo vértice é a origem do sistema e cujo eixo de simetria é o eixo [tex]O’Y’.[/tex]
[tex]{\color{#800000}(2)}[/tex] Translação de eixos coordenados
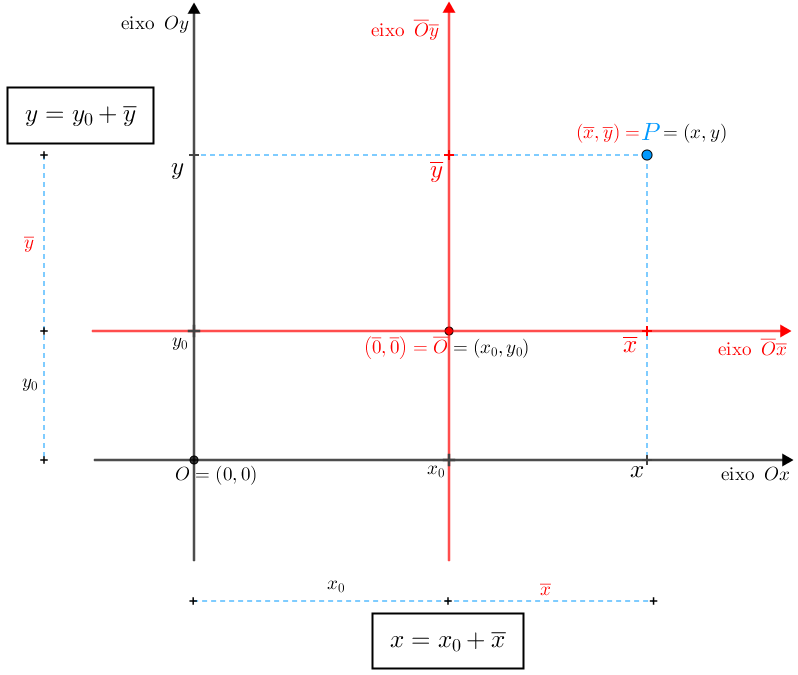
- Sejam [tex]xOy[/tex] um sistema de eixos ortogonais e [tex]\overline{O}=\left(x_0,y_0\right)[/tex] um ponto desse plano.
- Seja [tex]\overline{x}\overline{O}\overline{y}[/tex] um sistema de eixos cujos eixos [tex]\overline{O}\overline{x}[/tex] e [tex]\overline{O}\overline{y}[/tex] são paralelos aos eixos [tex]Ox[/tex] e [tex]Oy[/tex], respectivamente.
Se [tex](x, y)[/tex] são as coordenadas de um ponto [tex]P[/tex] no sistema [tex]xOy[/tex] e [tex]\left(\overline{x},\overline{y}\right)[/tex] são as coordenadas desse mesmo ponto [tex]P[/tex] no sistema [tex]\overline{x}\overline{O}\overline{y}[/tex], então essas coordenadas estão assim relacionadas:
[tex]\qquad \qquad \boxed{\begin{cases}
x=x_0+\overline{x}\\
y=y_0+\overline{y}
\end{cases}}\,.[/tex]
Se você não se lembra dessas relações, disponibilizamos uma figura para ajudar. Se precisar, é só clicar no botão abaixo!
Solução
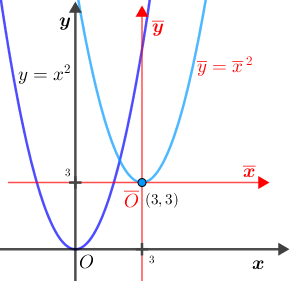
Para cada parábola, a partir da segunda, vamos fazer uma translação do sistema de eixos [tex]xOy[/tex] para um sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] no qual a origem [tex]\textcolor{red}{\overline{O}}[/tex] seja o vértice dessa parábola. No novo sistema, a parábola em questão terá como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}[/tex]; como conhecemos as coordenadas do vértice dessa parábola no sistema original [tex]xOy[/tex], a partir das equações de translação, conseguiremos escrever sua equação no sistema [tex]xOy.[/tex]
- Parábola 2:
- Parábola 3:
- Parábola 4:
- Parábola 5:
- Parábola 6:
- Parábola 7:
- Parábola 8:
|
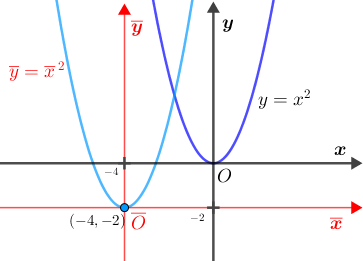
Pelo Lembrete 1, no sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] a parábola 2 tem como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}.[/tex] Pelo Lembrete 2, as equações de translação são: [tex]\qquad \begin{cases} \textcolor{red}{\overline{x}}=x-(-4)=x+4\\ \textcolor{red}{\overline{y}}=y-(-2)=y+2 \end{cases}\,.[/tex] Dessa forma, a equação da parábola 2 no sistema [tex]xOy[/tex] fica assim determinada: [tex]\qquad \textcolor{red}{\overline{y}=\overline{x}\,^2}\\ \qquad y+2=\left(x+4\right)^2\\ \qquad y=\left(x+4\right)^2-2\\ \qquad\fcolorbox{black}{#eee0e5}{$ y=x^2+8x+14$}\,.[/tex] |
|
|
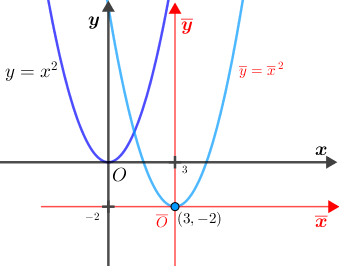
Pelo Lembrete 1, no sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] a parábola 3 tem como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}.[/tex] Pelo Lembrete 2, as equações de translação são: [tex]\qquad \begin{cases} \textcolor{red}{\overline{x}}=x-3\\ \textcolor{red}{\overline{y}}=y-(-2)=y+2 \end{cases}\,.[/tex] Dessa forma, a equação da parábola 3 no sistema [tex]xOy[/tex] fica assim determinada: [tex]\qquad \textcolor{red}{\overline{y}=\overline{x}\,^2}\\ \qquad y+2=\left(x-3\right)^2\\ \qquad y=\left(x-3\right)^2-2\\ \qquad\fcolorbox{black}{#eee0e5}{$ y=x^2-6x+7$}\,.[/tex] |
|
|
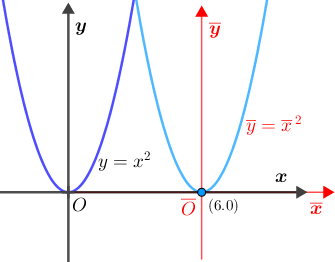
Pelo Lembrete 1, no sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] a parábola 4 tem como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}.[/tex] Pelo Lembrete 2, as equações de translação são: [tex]\qquad \begin{cases} \textcolor{red}{\overline{x}}=x-6\\ \textcolor{red}{\overline{y}}=y-0 \end{cases}\,.[/tex] Dessa forma, a equação da parábola 4 no sistema [tex]xOy[/tex] fica assim determinada: [tex]\qquad \textcolor{red}{\overline{y}=\overline{x}\,^2}\\ \qquad y-0=\left(x-6\right)^2\\ \qquad y=\left(x-6\right)^2\\ \qquad\fcolorbox{black}{#eee0e5}{$ y=x^2-12x+36$}\,.[/tex] |
|
|
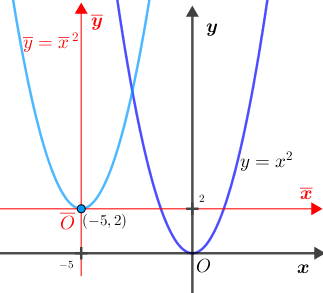
Pelo Lembrete 1, no sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] a parábola 5 tem como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}.[/tex] Pelo Lembrete 2, as equações de translação são: [tex]\qquad \begin{cases} \textcolor{red}{\overline{x}}=x-(-5)=x+5\\ \textcolor{red}{\overline{y}}=y-2 \end{cases}\,.[/tex] Dessa forma, a equação da parábola 5 no sistema [tex]xOy[/tex] fica assim determinada: [tex]\qquad \textcolor{red}{\overline{y}=\overline{x}\,^2}\\ \qquad y-2=\left(x+5\right)^2\\ \qquad y=\left(x+5\right)^2+2\\ \qquad\fcolorbox{black}{#eee0e5}{$ y=x^2+10x+27$}\,.[/tex] |
|
|
Pelo Lembrete 1, no sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] a parábola 6 tem como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}.[/tex] Pelo Lembrete 2, as equações de translação são: [tex]\qquad \begin{cases} \textcolor{red}{\overline{x}}=x-3\\ \textcolor{red}{\overline{y}}=y-3 \end{cases}\,.[/tex] Dessa forma, a equação da parábola 6 no sistema [tex]xOy[/tex] fica assim determinada: [tex]\qquad \textcolor{red}{\overline{y}=\overline{x}\,^2}\\ \qquad y-3=\left(x-3\right)^2\\ \qquad y=\left(x-3\right)^2+3\\ \qquad\fcolorbox{black}{#eee0e5}{$ y=x^2-6x+12$}\,.[/tex] |
|
|
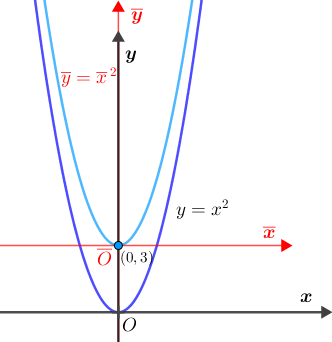
Pelo Lembrete 1, no sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] a parábola 7 tem como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}.[/tex] Pelo Lembrete 2, as equações de translação são: [tex]\qquad \begin{cases} \textcolor{red}{\overline{x}}=x-0\\ \textcolor{red}{\overline{y}}=y-3 \end{cases}\,.[/tex] Dessa forma, a equação da parábola 7 no sistema [tex]xOy[/tex] fica assim determinada: [tex]\qquad \textcolor{red}{\overline{y}=\overline{x}\,^2}\\ \qquad y-3=\left(x-0\right)^2\\ \qquad y=\left(x-0\right)^2+3\\ \qquad\fcolorbox{black}{#eee0e5}{$ y=x^2+3$}\,.[/tex] |
|
|
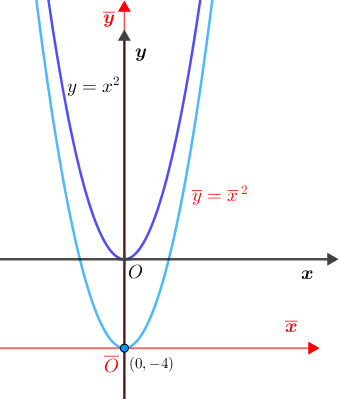
Pelo Lembrete 1, no sistema [tex]\textcolor{red}{\overline{x}\overline{O}\overline{y}}[/tex] a parábola 8 tem como equação [tex]\textcolor{red}{\overline{y}=\overline{x}\,^2}.[/tex] Pelo Lembrete 2, as equações de translação são: [tex]\qquad \begin{cases} \textcolor{red}{\overline{x}}=x-0\\ \textcolor{red}{\overline{y}}=y-(-4)=y+4 \end{cases}\,.[/tex] Dessa forma, a equação da parábola 8 no sistema [tex]xOy[/tex] fica assim determinada: [tex]\qquad \textcolor{red}{\overline{y}=\overline{x}\,^2}\\ \qquad y+4=\left(x-0\right)^2\\ \qquad y=\left(x-0\right)^2-4\\ \qquad\fcolorbox{black}{#eee0e5}{$ y=x^2-4$}\,.[/tex] |
|
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |