Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
(UECE – 2017) Sejam [tex] \, x \, [/tex] e [tex] \, y \, [/tex] números reais tais que [tex] 2x+5y=10[/tex].
Qual é o menor valor que a expressão [tex]x^2+y^2[/tex] pode assumir?

Ajuda
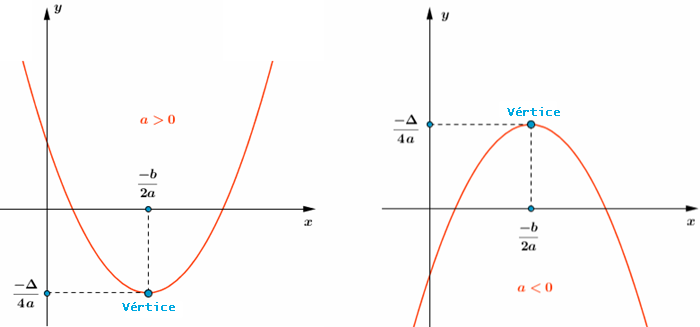
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a} \, [/tex] e [tex] \, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução 1
Sejam [tex] \, x \, [/tex] e [tex] \, y \, [/tex] números reais tais que [tex] 2x+5y=10[/tex] e seja [tex]\boxed{z= x^2+y^2}.[/tex]
De [tex] 2x+5y=10[/tex] segue que [tex]y=\dfrac{10-2x}{5}[/tex]; assim, podemos reescrever a expressão que define [tex]z[/tex] em função apenas de [tex]x:[/tex]
[tex]\qquad z= x^2+y^2[/tex]
[tex]\qquad z= x^2+\left(\dfrac{10-2x}{5} \right)^2[/tex]
[tex]\qquad z= x^2+\dfrac{100-40x+4x^2}{25}[/tex]
[tex]\qquad z=\dfrac{25 x^2+100-40x+4x^2}{25}[/tex]
[tex]\qquad z=\dfrac{1}{25} \cdot \left(29x^2-40x +100\right).[/tex]
Vamos determinar o menor valor de [tex]z[/tex] e para isso vamos considerar a função quadrática [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x)=29x^2-40x+100[/tex].
Observe que o coeficiente de [tex]x^2[/tex] da expressão que define [tex]f[/tex] é positivo; assim, utilizando as informações da Ajuda, concluímos que a concavidade da parábola do gráfico de [tex]f[/tex] é voltada para cima. Consequentemente, a segunda coordenada do vértice dessa parábola, digamos [tex]y_v[/tex], é o menor valor assumido pela função e, portanto, o menor valor de [tex]z[/tex] é [tex]\boxed{\dfrac{1}{25} \cdot y_v}.[/tex]
Vamos, então, calcular [tex]y_v[/tex]:
[tex]\qquad y_v=\dfrac{-\Delta}{4a}= \dfrac{-\left(b^2-4ac \right)}{4a}[/tex]
[tex]\qquad y_v=\dfrac{-\left((-40)^2-4\cdot 29 \cdot 100 \right)}{4\cdot 29}=\dfrac{-\left(1600-11600 \right)}{4\cdot 29}[/tex]
[tex]\qquad y_v=\dfrac{10 \, 000 }{4\cdot 29}=\dfrac{2500 }{29}[/tex].
Dessa forma, se denotarmos por [tex]z_{min}[/tex] o menor valor da expressão [tex]x^2+y^2[/tex], respeitadas as condições do problema, então:
[tex]\qquad z_{min}=\dfrac{1}{25} \cdot y_v=\dfrac{1}{25} \cdot \dfrac{2500 }{29}=\dfrac{100 }{29}.[/tex]
Assim, o valor procurado é [tex] \, \fcolorbox{black}{#ffd3d3}{$\dfrac{100 }{29}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Observe que a expressão [tex]2x+5y=10[/tex] representa uma reta em um plano cartesiano [tex]xOy.[/tex]
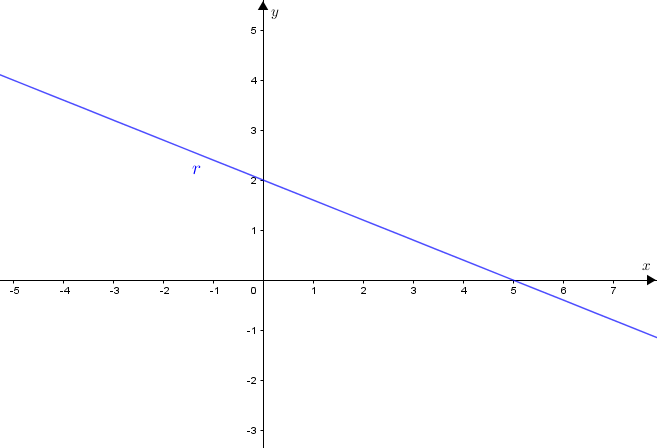
Repare que a reta [tex]r[/tex] e os eixos [tex]Ox[/tex] e [tex]Oy[/tex] definem um triângulo retângulo cujos catetos têm comprimentos [tex]2[/tex] e [tex]5[/tex] e a hipotenusa tem comprimento [tex]\sqrt{29}[/tex].
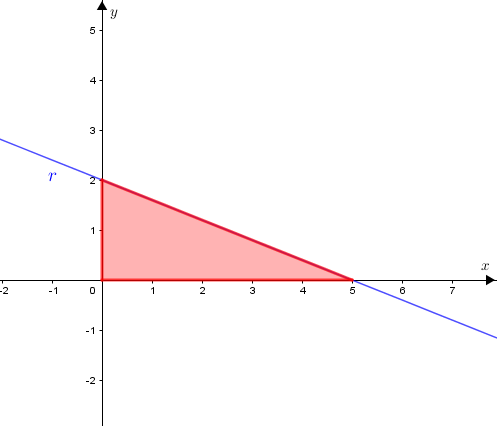
Por outro lado, sabemos que a distância de qualquer ponto [tex]P=(x,y)[/tex] à origem é dada por [tex]\sqrt{x^{2}+y^{2}}[/tex]; portanto, a expressão [tex]x^2+y^2[/tex] nos fornece o quadrado da distância de um ponto [tex]P[/tex] do plano cartesiano à origem.
- Assim, geometricamente, o que o problema está pedindo é o quadrado da distância entre a reta [tex]r[/tex] e a origem do sistema cartesiano, [tex]O=(0,0)\,.[/tex]
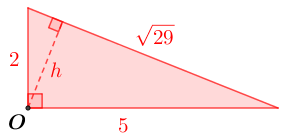
| Observe que a distância entre a reta [tex]r[/tex] e o ponto [tex]O[/tex] é a altura [tex]h[/tex] do triângulo vermelho que aparece na figura anterior, e que destacamos na figura ao lado, com relação à sua hipotenusa. Nesse caso, podemos utilizar a relação métrica no triângulo retângulo que nos garante que o produto entre os comprimentos da hipotenusa e da altura é igual ao produto dos comprimentos dos dois catetos. Assim: [tex]\qquad \sqrt{29}\cdot h = 2\cdot5[/tex] [tex]\qquad h=\dfrac{10}{\sqrt{29}}\approx 1,86[/tex]. Portanto, [tex]\, \fcolorbox{black}{#ffd3d3}{$h^{2}=\dfrac{100}{29}$}\,[/tex]. |
 |
Um applet para ajudar
Instruções:
(1) Espere o aplicativo carregar completamente.
(2) Clique no ponto P, mantenha o mouse pressionado e faça o movimento.
(3) Para retornar à posição inicial, clique no centro das setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Solução elaborada pelos Moderadores do Blog.
Solução 3
Duas observações iniciais:
- A igualdade [tex]2x+5y=10[/tex] define uma reta [tex]r[/tex] em um plano cartesiano [tex]xOy.[/tex]
- A distância de qualquer ponto [tex]P=(x,y)[/tex] à origem é dada por [tex]\sqrt{x^{2}+y^{2}}[/tex] e, portanto, a expressão [tex]x^2+y^2[/tex] nos fornece o quadrado da distância de um ponto [tex]P[/tex] do plano cartesiano à origem.
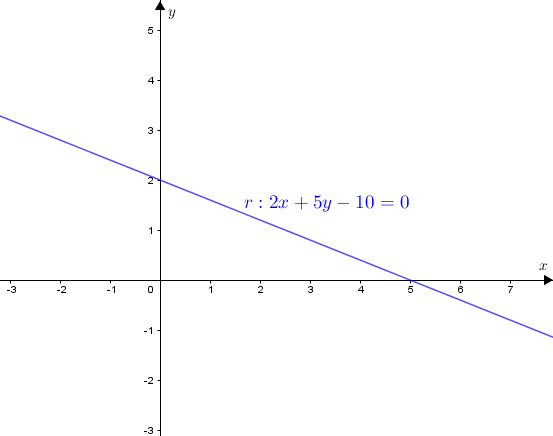
Assim, geometricamente, o que o problema está pedindo é o quadrado da distância entre a reta [tex]r[/tex] e a origem do sistema cartesiano, [tex]O=(0,0)\,.[/tex]
- Vamos então calcular a distância entre a reta [tex]r[/tex] e ao ponto [tex]O.[/tex]
A fórmula que nos fornece diretamente a distância [tex]d[/tex] entre um ponto [tex]P=(x_0,y_0)[/tex] e uma reta definida por [tex]ax+by+c=0[/tex] é:
[tex]\qquad \qquad d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}.[/tex]
Dessa forma, a distância entre a reta [tex]r[/tex] e o ponto [tex]O=(0,0)\,[/tex] pode ser assim calculada:
[tex]\qquad \qquad d=\dfrac{|2\times 0+5 \times 0-10|}{\sqrt{2^2+5^2}}[/tex]
[tex]\qquad \qquad d=\dfrac{10}{\sqrt{2^2+5^2}}[/tex]
[tex]\qquad \qquad \boxed{d=\dfrac{10}{\sqrt{29}}}.[/tex]
Com isso, temos que o quadrado da distância entre [tex]r[/tex] e o ponto [tex]O=(0,0)\,[/tex] é [tex]\, \, \fcolorbox{black}{#ffd3d3}{$\dfrac{100}{29}$}\, [/tex], que é a resposta do problema.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |