.Problema para ajudar na escola: Duas rosquinhas

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)

---

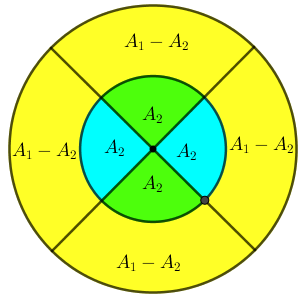
A figura a seguir mostra duas circunferências concêntricas, uma de raio [tex]4\, \text{cm}[/tex] e outra de raio [tex]8\, \text{cm}[/tex], e dois diâmetros perpendiculares entre si.

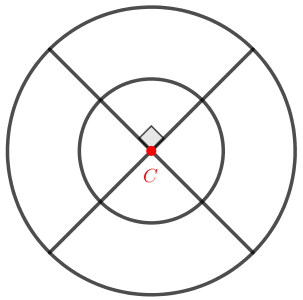
Essa figura foi colorida e recortada adequadamente, de modo a formar as duas “rosquinhas” mostradas na figura abaixo.
Qual a medida da área de cada “rosquinha” que aparece na figura?

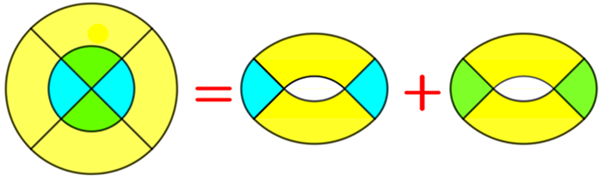
Solução 1

---

Observe que na figura inicial temos quatro ângulos centrais com a mesma medida, [tex]90^\circ[/tex]; logo, os quatro arcos definidos em cada circunferência têm consequentemente a mesma medida. Dessa forma, as áreas dos quatro setores circulares definidos pela circunferência externa têm a mesma medida, digamos [tex]A_1[/tex], assim como os quatro setores circulares definidos pela circunferência interna têm a mesma medida, digamos [tex]A_2.[/tex]

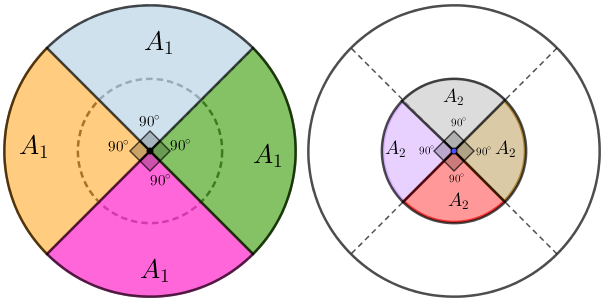
Se você gosta de fazer contas, note que [tex]A_1[/tex] é a medida de um quarto da circunferência externa e [tex]A_2[/tex] é a medida de um quarto da circunferência interna. ou seja,

[tex]\boxed{A_1=\dfrac{\pi\times 8^2}{4}=16\pi\, \text{cm}^2}\qquad [/tex] e [tex]\qquad \boxed{A_2=\dfrac{\pi\times 4^2}{4}=4\pi\, \text{cm}^2}.[/tex]

Vamos observar as duas “rosquinhas”.

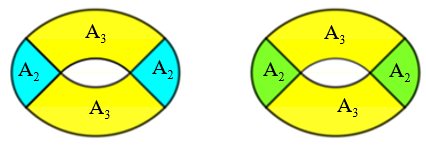
Note que já temos as medidas das áreas das respectivas regiões coloridas de azul e de verde de cada uma delas:
[tex]\qquad \qquad 2 \times A_2=8\pi\, \text{cm}^2. \qquad \textcolor{#800000}{(i)}[/tex]
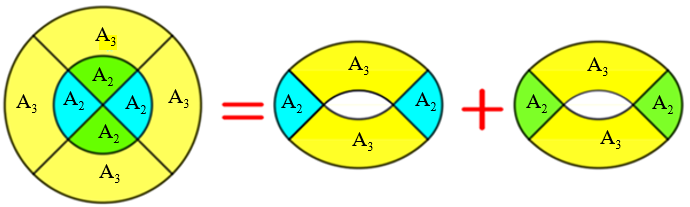
Precisamos agora calcular a medida da área da região amarela e a figura abaixo nos mostra que, em cada “rosquinha”, a região amarela corresponde a duas regiões amarelas da figura original antes de ser cortada, ou seja:
[tex]\qquad \qquad 2 \times A_3=2 \times \left(A_1-A_2 \right)= 2 \times \left(16\pi-4\pi \right)=24\pi\, \text{cm}^2. \qquad \textcolor{#800000}{(ii)}[/tex]

Por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], concluímos que a medida [tex]A[/tex] da área de cada “rosquinha” é [tex]A=8\pi+24\pi= \fcolorbox{black}{#eee0e5}{$32\pi\, \text{cm}^2$}\,.[/tex]

---

Solução elaborada pelos Moderadores do Blog.

Solução 2

---

Um olhar atento e crítico nos permite calcular a medida da área de cada “rosquinha”, sem muitas contas. Mas a observação inicial da primeira solução é útil para nossa análise; portanto, observe que na figura inicial temos quatro ângulos centrais com a mesma medida, [tex]90^\circ[/tex]. Com isso, as áreas das quatro regiões coloridas do círculo maior têm a mesma medida, digamos [tex]A_1[/tex], assim como as áreas das quatro regiões coloridas do círculo menor têm a mesma medida, digamos [tex]A_2.[/tex]

Dessa forma, a área de cada rosquinha é [tex]\boxed{A_3+A_3+A_2+A_2=2\times A_3+2 \times A_2}.[/tex]

Perceba que, mesmo coloridas com cores diferentes, as medidas das áreas das regiões azuis e verdes são todas iguais; logo, a partir da figura a seguir, concluímos que a área de cada “rosquinha” corresponde à metade da área do círculo maior:
[tex]\qquad 2\times A_3+2 \times A_2=2\times\left(A_1-A_2\right)+2\times A_2=2\times A_1.[/tex]

Portanto, se a medida da área de cada rosquinha que aparece na figura for denotada por [tex]A[/tex], segue que:
[tex]\qquad A=\dfrac{\pi \times 8^2 }{2}=\fcolorbox{black}{#eee0e5}{$32\pi\, \text{cm}^2$}[/tex] .

Na Solução 2, não utilizamos o raio do círculo menor. Qual foi a utilidade desse dado na segunda solução?

---

Solução elaborada pelos Moderadores do Blog.