✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
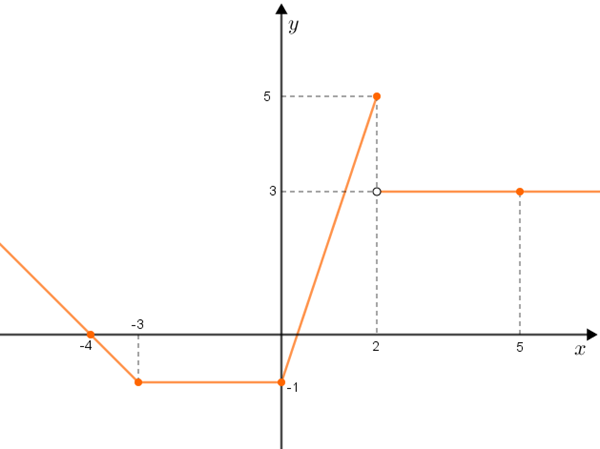
Determine [tex]f(x) \, [/tex], sabendo que [tex]f[/tex] é a função de [tex] \mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] cujo gráfico aparece esboçado abaixo.
Solução
A função [tex]f[/tex] é o que chamamos de uma função definida por partes ou por várias sentenças. Particularmente, supondo que a tendência linear observada à esquerda e à direita do gráfico se mantenha nos intervalos [tex]]-\infty, -3 \, ] [/tex] e [tex]] \, 2 , \infty[ [/tex], respectivamente, devemos calcular quatro expressões lineares para [tex] f(x) \, [/tex].
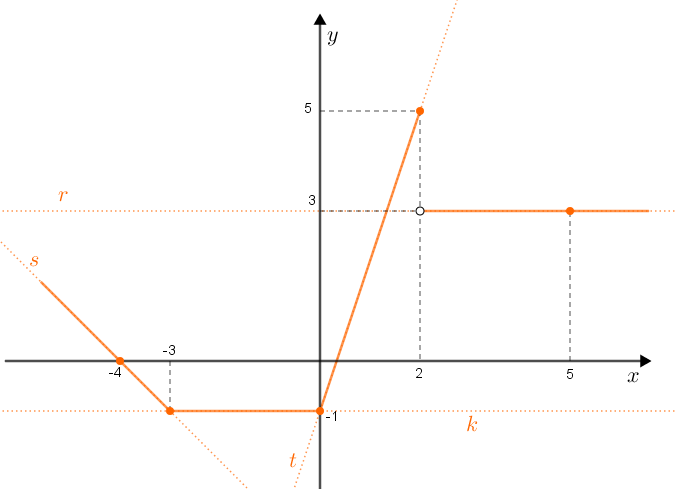
Observe inicialmente que as quatro expressões de [tex]f(x) \, [/tex] são as expressões que definem as retas [tex] k, \, r, \, s[/tex] e [tex]t[/tex] mostradas na figura a seguir.
Vamos aos cálculos.
- A reta [tex]\textcolor{#FF6600}{k}[/tex] é paralela ao eixo [tex]Ox[/tex] e corta o eixo [tex]Oy[/tex] no ponto de coordenadas [tex](0,-1)[/tex]. Como os pontos de [tex]\textcolor{#FF6600}{k}[/tex] têm coordenadas da forma [tex](x,-1)[/tex], com [tex]x[/tex] um número real qualquer, então esta é a equação de [tex]\textcolor{#FF6600}{k}[/tex]:
- A reta [tex]\textcolor{#FF6600}{r}[/tex] também é paralela ao eixo [tex]Ox[/tex], mas corta o eixo [tex]Oy[/tex] no ponto de coordenadas [tex](0,3)[/tex]. Assim, os seus pontos têm coordenadas da forma [tex](x,3)[/tex], com [tex]x[/tex] um número real qualquer e, então, esta é a sua equação:
- A reta [tex]\textcolor{#FF6600}{s}[/tex] passa pelos pontos de coordenadas [tex](-4,0)[/tex] e [tex](-3,-1)[/tex]; assim, as coordenadas desses dois pontos satisfazem a equação de [tex]\textcolor{#FF6600}{s}[/tex].
Dessa forma, se a equação de [tex]\textcolor{#FF6600}{s}[/tex] é da forma [tex]y=ax+b[/tex], com [tex]a[/tex] e [tex]b[/tex] números reais, temos que: - A reta [tex]\textcolor{#FF6600}{t}[/tex] passa pelos pontos de coordenadas [tex](0,-1)[/tex] e [tex](2,5)[/tex]; então, as coordenadas desses pontos satisfazem a equação de [tex]\textcolor{#FF6600}{t}[/tex].
Assim, se essa equação for da forma [tex]y=mx+n[/tex], com [tex]m[/tex] e [tex]n[/tex] números reais, temos que:
[tex]\qquad \textcolor{#FF6600}{k}: y=-1. \qquad \qquad \textcolor{#FF6600}{(i)}[/tex]
[tex]\qquad \textcolor{#FF6600}{r}: y=3. \qquad \qquad \textcolor{#FF6600}{(ii)}[/tex]
[tex]\qquad \boxed{0=-4a+b} \quad[/tex] e [tex]\quad \boxed{-1=-3a+b} \, .[/tex]
Da primeira equação, obtemos que [tex]b=4a[/tex] e, substituindo essa expressão na segunda equação, segue que:
[tex]\qquad -1=-3a+4a[/tex]
[tex]\qquad a=-1[/tex],
donde concluímos que [tex]b=4\times (-1)=-4[/tex]. Assim, a equação de [tex]\textcolor{#FF6600}{s}[/tex] é
[tex]\qquad \textcolor{#FF6600}{s}: y=-x-4. \qquad \qquad \textcolor{#FF6600}{(iii)}[/tex]
[tex]\qquad \boxed{-1=0m+n} \quad[/tex] e [tex]\quad \boxed{5=2m+n} \, .[/tex]
Da primeira equação, segue que [tex]n=-1[/tex] e, substituindo esse valor na segunda equação, tem-se que:
[tex]\qquad 5=2m-1[/tex]
[tex]\qquad m=3[/tex],
Logo:
[tex]\qquad \textcolor{#FF6600}{t}: y=3x-1. \qquad \qquad \textcolor{#FF6600}{(iv)}[/tex]
Pronto, já podemos definir completamente a lei de formação da função [tex]f.[/tex] Por [tex] \textcolor{#FF6600}{(i)}[/tex], [tex] \textcolor{#FF6600}{(ii)}[/tex], [tex] \textcolor{#FF6600}{(iii)}[/tex] e [tex] \textcolor{#FF6600}{(iv)}[/tex], concluímos que:
[tex]f(x)=\begin{cases} -x-4, \text{ se } x\in \, ]-\infty, -3 \, ] \\
-1, \text{ se } x\in \, ]-3, 0 \, ] \\
3x-1, \text{ se } x\in \, ] \, 0, 2 \, ] \\
3, \text{ se } x\in \, ] \, 2,+\infty]
\end{cases} \, \, [/tex].
Note que o ponto [tex](-3,-1)[/tex] é ponto tanto da reta [tex]\textcolor{#FF6600}{s}[/tex] como da reta [tex]\textcolor{#FF6600}{k}[/tex]; então, poderíamos também definir [tex]f(x)[/tex] assim :
[tex]f(x)=\begin{cases} -x-4, \text{ se } x\in \, ]-\infty, -3 \, [ \\
-1, \text{ se } x\in \, [-3, 0 \, ] \\
3x-1, \text{ se } x\in \, ] \, 0, 2 \, ] \\
3, \text{ se } x\in \, ] \, 2,+\infty]
\end{cases} \, \, [/tex].
Raciocinando de maneira análoga, com relação ao ponto [tex](0,-1)[/tex] e às retas [tex]\textcolor{#FF6600}{k}[/tex] e [tex]\textcolor{#FF6600}{t}[/tex], poderíamos também escrever:
[tex]f(x)=\begin{cases} -x-4, \text{ se } x\in \, ]-\infty, -3 \, ] \\
-1, \text{ se } x\in \, ]-3, 0 \, [ \\
3x-1, \text{ se } x\in \, [ \, 0, 2 \, ] \\
3, \text{ se } x\in \, ] \, 2,+\infty]
\end{cases}[/tex]
ou, ainda,
[tex]f(x)=\begin{cases} -x-4, \text{ se } x\in \, ]-\infty, -3 \, [ \\
-1, \text{ se } x\in \, [-3, 0 \, [ \\
3x-1, \text{ se } x\in \, [ \, 0, 2 \, ] \\
3, \text{ se } x\in \, ] \, 2,+\infty]
\end{cases} \, \, [/tex].
CUIDADO com o ponto [tex](2,5)[/tex]. Ele pertence apenas à reta [tex]\textcolor{#FF6600}{t}[/tex] !
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
