✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
Na marcenaria do seu Joaquim, qualquer pedacinho de madeira que sobre de alguma encomenda é aproveitado.
Depois da entrega de uma grande encomenda, seu Joaquim percebeu que sobraram vários pedaços de madeira, na forma de paralelepípedos retorretângulos com dimensões "[tex]6\,\text{cm}[/tex] por [tex]15\,\text{cm}[/tex] por [tex]20\,\text{cm}[/tex]".
Também para aproveitar restinhos de tinta, ele pintou os paralelepípedos e resolveu montar cubos para decoração com os paralelepípedos coloridos.
Quantos desses paralelepípedos coloridos serão necessários para que seu Joaquim monte o menor cubo possível, mantendo o tamanho original dos pequenos paralelepípedos?

Lembrete
✐ O volume de um paralelepípedo retorretângulo cujos lados expressos na mesma unidade de comprimento medem [tex]a \, ; \, b \, ; \, c \, [/tex] é o produto dessas três medidas:
[tex]\qquad \qquad \boxed{V=a \cdot b \cdot c} \, .[/tex]
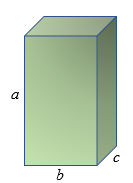
Particularmente, um cubo é um paralelepípedo retorretângulo cujos lados têm o mesmo comprimento. Assim, o volume de um cubo cujos lados medem [tex]x[/tex] é
[tex]\qquad \qquad \boxed{V=x \cdot x \cdot x=x^3} \, .[/tex]
Solução
Seja [tex]l[/tex] o comprimento em centímetros do menor cubo que o seu Joaquim conseguirá montar utilizando os pequenos paralelepípedos.
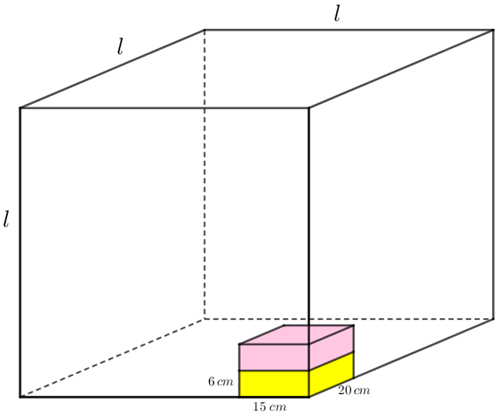
- Como o tamanho original dos paralelepípedos deverá ser mantido, as medidas [tex]6\,\text{cm}[/tex], [tex]15\,\text{cm}[/tex] e [tex]20\,\text{cm}[/tex] deverão caber no comprimento [tex]l\; \text{cm}[/tex] dos lados do cubo a ser montado. Assim, [tex]l[/tex] é um múltiplo comum de [tex]6\,[/tex], [tex]15\,[/tex] e [tex]20\,[/tex].
- Como seu Joaquim vai montar o menor cubo possível, então [tex]l[/tex] é o mínimo múltiplo comum entre [tex]6\,[/tex], [tex]15\,[/tex] e [tex]20\,[/tex], ou seja, [tex]l=mmc(6,15,20)[/tex].
Fatorando simultaneamente os números [tex]6,15[/tex] e [tex]20[/tex], obtemos o [tex]mmc[/tex] deles:
[tex]\qquad \begin{array}{r r r |l}
6 & 15 & 20 &2\\
3 & 15 & 10 &2\\
3 & 15 & 5 &3\\
1 & 5 & 5 &5\\
1 & 1 & 1 &\overline{2\times 2\times 3 \times 5=60}\\
\end{array}[/tex]
Logo, [tex]\boxed{l=60\,\text{cm}}\,[/tex] e o menor cubo que o seu Joaquim conseguirá montar como esses paralelepípedos inteiros deve ter lados medindo [tex]60[/tex] centímetros.
Mas o problema nos pede para calcular a quantidade de paralelepípedos utilizados na montagem de cada cubo.
Então, vamos lá!
Observe que:
- O volume de cada paralelepípedo utilizado é [tex]6 \times 15 \times 20=1800\text{ cm}^3[/tex].
- O volume de um cubo a ser montado é [tex]60 \times 60 \times 60=216000\text{ cm}^3[/tex].
Dessa forma, se [tex]n[/tex] for o número de paralelepípedos utilizados na montagem de cada cubo, segue que:
[tex]\qquad 1800n=216000\\
\qquad n=\dfrac{216000}{1800}\\
\qquad n=120\,.[/tex]
Assim, seu Joaquim utilizará [tex]\fcolorbox{black}{#eee0e5}{$120$}[/tex] paralelepípedos na montagem de cada cubo de decoração.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
