Problema
(A partir do 1º ano do E. M.- Nível de dificuldade: Difícil)
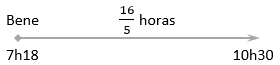
Bene deixou a cidade de Benápolis em direção à cidade de Cenápolis às 7h18min, chegando ao seu destino às 10h30min, caminhando sempre a uma velocidade constante.
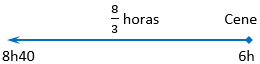
Nesse mesmo dia, Cene saiu de Cenápolis às 6 horas, chegando em Benápolis às 8h40, andando pela mesma estrada também a uma velocidade constante.
A única estrada que liga as cidades de Benápolis e Cenápolis está sendo asfaltada e entre as duas cidades ainda tem um trecho não asfaltado. Bene e Cene chegaram simultaneamente ao início desse trecho não asfaltado, cada um de um lado; mas Cene saiu do trecho não asfaltado um minuto antes que Bene.

A que horas Bene e Cene chegaram no trecho não asfaltado da estrada?
Adaptado da Revista da Quantum.
Lembrete

Quando um objeto está em movimento, ele muda de posição ao longo do percurso. A velocidade desse objeto é definida levando-se em consideração o espaço que ele percorreu em um determinado intervalo de tempo, ou seja, velocidade é a grandeza que mede quão rápido um objeto se desloca.
Se conhecermos a extensão do percurso e o tempo gasto pelo objeto para percorrê-lo, podemos dividir o espaço percorrido pelo tempo total de percurso e esse quociente chamamos velocidade média do objeto.
Se a velocidade de um objeto é constante, ela é igual à velocidade média do objeto nesse movimento, ou seja:
[tex]\boxed{\text{velocidade}=\frac{\text{distância percorrida}}{\text{tempo gasto}}}[/tex].
Chamando a velocidade de [tex]v[/tex], a distância percorrida de [tex]d[/tex] e o tempo gasto de [tex]t[/tex], temos [tex]\boxed{v=\frac{d}{t}}[/tex] e, nesse caso, [tex]\boxed{d=v\times t}[/tex].
É importante darmos atenção às unidades de medida. Se, por exemplo, a velocidade é em quilômetros/hora, a distância é em quilômetros e o tempo é em horas.
Solução
Como Bene saiu de Benápolis às [tex]7h18min[/tex] e chegou em Cenápolis às [tex]10h30min[/tex], ele completou o trajeto em [tex]3[/tex] horas e [tex]12[/tex] minutos.
Por sua vez, Cene saiu de Cenápolis às [tex]6h[/tex] e chegou em Benápolis às [tex]8h40min[/tex]; então ele completou o trajeto em [tex]2[/tex] horas e [tex]40[/tex] minutos.
Vamos calcular os tempos de caminhada em horas e para isso vamos converter [tex]12[/tex] minutos e [tex]40[/tex] minutos em horas, utilizando duas regrinhas de três simples.
|
[tex]\begin{array}{c c c} \; 1\text{ hora} & \text{————–} & 60\text{ minutos} \\ \; b & \text{————–} & 12\text{ minutos} \end{array}[/tex] Dessa forma, obtemos que [tex]\boxed{60b= 12}[/tex], donde:
|
[tex]\begin{array}{c c c} \quad 1\text{ hora} & \text{————–} & 60\text{ minutos} \qquad \\ \quad c & \text{————–} & 40\text{ minutos} \qquad \end{array}[/tex] Dessa forma, obtemos que [tex]\boxed{60c= 40}[/tex], donde:
|
Se denotarmos a distância em quilômetros entre as duas cidades por [tex]d[/tex], podemos calcular a velocidade com que Bene e Cene estavam caminhando, já que essas velocidades são constantes:
[tex]\qquad v_B=\dfrac{d}{\frac{16}{5}}=\dfrac{5d}{16}\,\text{ km/h}\qquad \quad [/tex] e [tex]\quad\qquad v_C=\dfrac{d}{\frac{8}{3}}=\dfrac{3d}{8}\,\text{ km/h}\,.[/tex]
Com essas velocidades, podemos determinar o comprimento em quilômetros do trecho não asfaltado da estrada, pois sabemos que Cene atravessou esse trecho um minuto mais rápido que Bene. Para isso, vamos fazer mais duas regras de três simples para determinar os respectivos tempos [tex]t’_B\,[/tex] e [tex]\,t’_C[/tex] que Bene e Cene levaram para percorrer o trecho não asfaltado, cujo comprimento em quilômetros vamos denotar por [tex]l\,.[/tex]
|
Como a velocidade de Bene é de [tex]\dfrac{5d}{16}\,\text{ km/h}[/tex], em uma hora ele percorre [tex]\dfrac{5d}{16}[/tex] quilômetros. Logo: [tex]\begin{array}{c c c} \qquad 1\text{ hora} & \text{————–} & \dfrac{5d}{16}\text{ km} \\ \qquad t’_B & \text{————–} & l\text{ km} \end{array}[/tex] Dessa forma, obtemos que [tex]\boxed{t’_B\cdot\dfrac{5d}{16} = l}[/tex], donde: |
Como a velocidade de Cene é de [tex]\dfrac{3d}{8}\,\text{ km/h}[/tex], em uma hora ele percorre [tex]\dfrac{3d}{8}[/tex] quilômetros. Logo: [tex]\begin{array}{c c c} \qquad 1\text{ hora} & \text{————–} & \dfrac{3d}{8}\text{ km} \\ \qquad t’_C & \text{————–} & l\text{ km} \end{array}[/tex] Dessa forma, obtemos que [tex]\boxed{t’_C\cdot\dfrac{3d}{8} = l}[/tex], donde: |
Mas Cene atravessou o trecho não asfaltado um minuto mais rápido que Bene; logo, como [tex]1 \text{ minuto} =\frac{1}{60} \text{horas}[/tex], segue que:
[tex] \quad t’_B-t’_C=\dfrac{1}{60}\\
\quad \dfrac{16l}{5d}-\dfrac{8l}{3d}=\dfrac{1}{60}\\
\quad \dfrac{48l-40l}{15d}=\dfrac{1}{60}\\
\quad \dfrac{8l}{15d}=\dfrac{1}{60}\\
\quad l=\dfrac{15d}{8\cdot 60}\\
\quad l=\dfrac{d}{32}\,.[/tex]
Como já conhecemos o comprimento do trecho não asfaltado, vamos supor que [tex]x[/tex] seja a distância em quilômetros de Benápolis ao início do trecho não asfaltado e [tex]y[/tex] seja a distância em quilômetros de Cenápolis ao início do trecho não asfaltado, conforme ilustra a próxima figura.
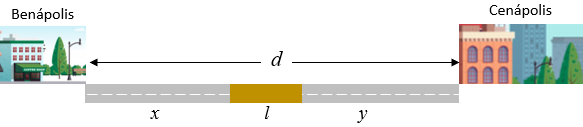
Como [tex]d[/tex] é a distância em quilômetros entre Benápolis e Cenápolis, temos que:
[tex]\quad x+l+y=d\\
\quad x+\dfrac{d}{32}+y=d\\
\quad x+y=d-\dfrac{d}{32}\\
\quad x+y=\dfrac{31d}{32}\,. \qquad \textcolor{#800000}{(i)}
[/tex]
Finalmente, vamos supor que [tex]H[/tex] tenha sido o horário exato da chegada de Bene e Cene ao trecho não asfaltado.
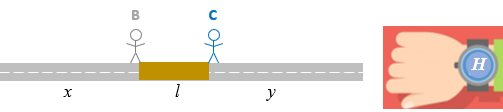
Agora, perceba que:
- Como Bene saiu de Benápolis às [tex]7h18mim[/tex], ele levou um tempo de [tex]H-(7+\frac{18}{60})[/tex] horas para percorrer a distância [tex]x[/tex].
- Como Cene saiu de Cenápolis às [tex]6h[/tex], ele levou um tempo de [tex]H-6[/tex] horas para percorrer a distância [tex]y[/tex].
Por outro, conhecemos a velocidade com que Bene e Cene percorreram o trajeto e essa velocidade foi constante. Dessa forma, conseguimos determinar [tex]x[/tex] e [tex]y[/tex]:
[tex]\qquad x=\dfrac{5d}{16} \cdot \left[H-\left(7+\dfrac{18}{60}\right)\right]=\dfrac{5d}{16} \cdot \left(H-\dfrac{73}{10}\right)\\
\qquad
[/tex]
[tex]\qquad y=\dfrac{3d}{8} \cdot \left(H-6\right)[/tex].
Assim, segue de [tex]\textcolor{#800000}{(i)}[/tex] que:
[tex]\quad x+y=\dfrac{31d}{32}\\
\quad \dfrac{5d}{16} \cdot \left(H-\dfrac{73}{10}\right)+\dfrac{3d}{8} \cdot \left(H-6\right)=\dfrac{31d}{32}\\
\quad \dfrac{5d}{16} \cdot \left(H-\dfrac{73}{10}\right)+\dfrac{6d}{16} \cdot \left(H-6\right)=\dfrac{31d}{32}\\
\quad \dfrac{d}{16} \cdot \left[5\cdot \left(H-\dfrac{73}{10}\right)+6 \cdot \left(H-6\right)\right]=\dfrac{31d}{32}\\
\quad 2 \cdot \left(5H-\dfrac{73}{2}+6H-36\right)=31\\
\quad 2 \cdot \left(11H-\dfrac{145}{2}\right)=31\\
\quad 22H-145=31\\
\quad 22H=176\\
\quad H=8\,.[/tex]
Portanto, Bene e Cene chegaram no trecho não asfaltado da estrada exatamente às [tex]\fcolorbox{black}{#eee0e5}{$8 \text{ horas}$}\,.[/tex]

Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |