✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Médio)
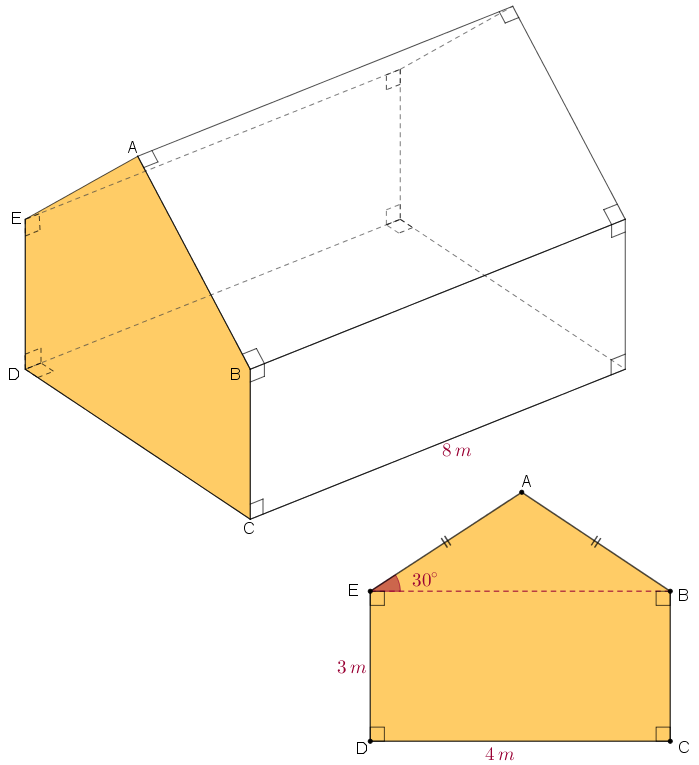
A figura mostra um dos celeiros para armazenamento de grãos de uma propriedade rural.
Supondo que a parte interna do celeiro em questão é totalmente aproveitável para armazenamento, determinar o volume máximo de grãos que podem ser armazenados nesse celeiro.
Solução 1
Observe que o celeiro de armazenamento de que trata o problema tem a forma de um prisma reto de base pentagonal, conforme podemos observar na figura abaixo.
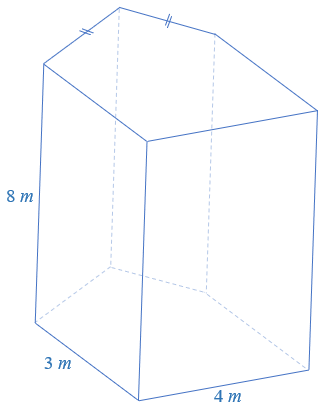
Dessa forma, o volume máximo de grãos que podem ser armazenados nesse celeiro é o volume [tex]V[/tex] desse prisma, que sabemos ser dado pelo produto entre a área da sua base e a sua altura:
[tex]\qquad V=\text{área da base}\times \text{altura} \, .[/tex]
Como conhecemos a altura do prisma, [tex]8 \, m \, [/tex], precisamos determinar a área [tex]A_p[/tex] do pentágono mostrado abaixo, área esta que é a soma das áreas do triângulo [tex]ABE[/tex] e do retângulo [tex]BCDE[/tex]: [tex]\boxed{A_p=A_t+A_r} \, .[/tex]
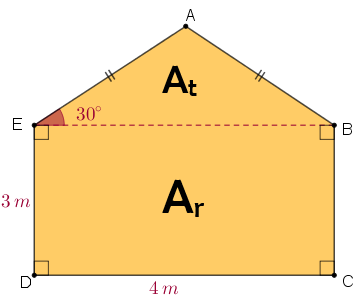
- A área [tex]A_r[/tex] é facilmente obtida: [tex]\boxed{A_r=3\times4=12 \, m^2} \, .\qquad \textcolor{#800000}{(i)}[/tex]
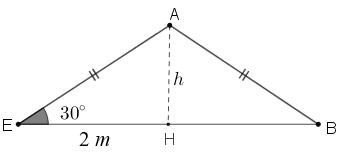
- Para calcular [tex]A_t[/tex], vamos obter a altura [tex]AH[/tex] relativa ao lado [tex]EB[/tex] do triângulo [tex]ABE[/tex].
Observe que [tex]ABE[/tex] é um triângulo isósceles; assim, como o segmento [tex]AH[/tex] é a altura relativa ao lado [tex]EB[/tex], então o ponto [tex]H[/tex] divide o lado [tex]EB[/tex] em dois segmentos congruentes de comprimento [tex]\dfrac{4}{2}=2 \, m \, .[/tex]
Logo, [tex]\text{tg} \, 30^\circ=\dfrac{h}{2}[/tex], donde obtemos que:
[tex]\qquad \quad h=2 \times \text{tg} \, 30^\circ= 2 \times \dfrac{\sqrt{3}}{3}=\dfrac{2\sqrt{3}}{3} \, m \, .[/tex]
Pronto, já podemos obter [tex]A_t[/tex]:
[tex]\qquad \qquad \boxed{A_t=\dfrac{4 \times \frac{2\sqrt{3}}{3}}{2}=\dfrac{4\sqrt{3}}{3} \, m^2} \, .\qquad \textcolor{#800000}{(ii)} [/tex]
Com isso, por [tex]\textcolor{#800000}{(i)} \, [/tex] e [tex] \, \textcolor{#800000}{(ii)}[/tex]:
[tex]\quad \qquad A_p=A_t+A_r=\left(\dfrac{4\sqrt{3}}{3}+12\right) \, m^2[/tex]
e, portanto, o volume do prisma é:
[tex]\qquad V=\text{área da base}\times \text{altura}[/tex]
[tex]\qquad V=\left(\dfrac{4\sqrt{3}}{3}+12 \right) \times 8[/tex]
[tex]\qquad V=\dfrac{32\sqrt{3}+288}{3} \, m^3 \, . [/tex]
Então, o volume máximo de grãos que podem ser armazenados no celeiro é de aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$114 \, m^3$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Poderíamos também tratar geometricamente o celeiro de armazenamento como um sólido composto por um paralelepípedo e um prisma triangular reto, conforme podemos observar na figura abaixo.
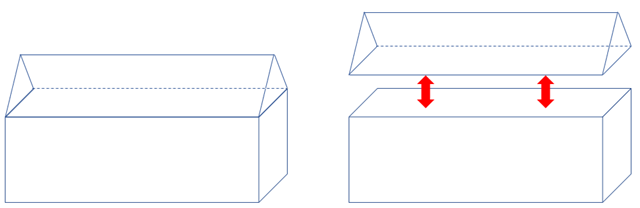
Desse modo, o volume máximo de grãos que podem ser armazenados no celeiro é o volume [tex]V[/tex] desse prisma, que é a soma dos volumes do paralelepípedo e do prisma triangular.
Aproveitem os cálculos acima e concluam que o volume do celeiro também poderia ser calculado desta maneira:
[tex]\qquad V=\text{volume do paralelepípedo} + \text{volume do prisma triangular}[/tex]
[tex]\qquad V=\left(4 \times 8 \times 3 \right)+\left( \dfrac{4\times \frac{2\sqrt{3}}{3}}{2}\times 8 \right)[/tex]
[tex]\qquad V=96+\dfrac{32\sqrt{3}}{3}[/tex]
[tex]\qquad V=\dfrac{288+32\sqrt{3}}{3} \, m^3 \, . [/tex]
Novamente, o volume máximo de grãos que podem ser armazenados no celeiro é de aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$114 \, m^3$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
