✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio )
Em uma malha quadriculada, foi construído um triângulo isósceles colorido de amarelo e, sobre cada lado desse triângulo, foram construídos triângulos coloridos de azul, conforme mostra a figura. (Considere que os vértices dos triângulos construídos são vértices de quadradinhos da malha.)
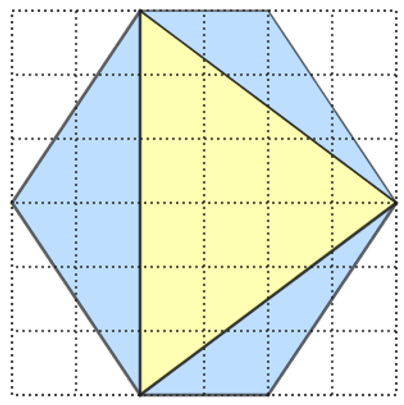
(a) Sabendo-se que os lados dos quadradinhos da malha medem [tex]2,1 \, [/tex]cm cada, determinar toda a área colorida de azul.
(b) Justifique a afirmação de que o triângulo amarelo é isósceles.
Solução
(a) Uma das maneiras de se calcular a área da região colorida de azul é calcular diretamente a área dos três triângulos coloridos de azul: triângulos [tex]T_1, T_2, \, T_3[/tex], cujas áreas denotaremos por [tex]A_1, A_2, \, A_3[/tex], respectivamente.
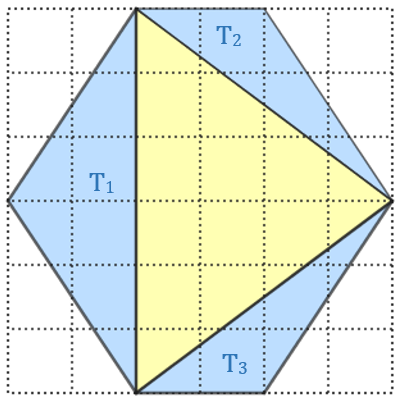
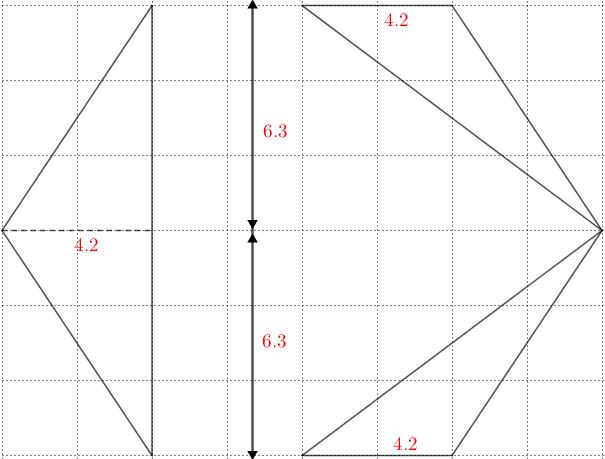
Considerando que os lados dos quadradinhos da malha medem [tex]2,1 \, [/tex]cm cada, as medidas indicadas na figura ao lado podem ajudar no cálculo das áreas.
- Área do triângulo [tex]T_1[/tex]:
- Área dos triângulos [tex]T_2[/tex] e [tex]T_3[/tex]:
[tex]\qquad A_1=\dfrac{12,6 \times 4,2}{2}=26,46 \text{ cm}^2[/tex].
[tex]\qquad A_2=A_3=\dfrac{6,3 \times 4,2}{2}=13,23 \text{ cm}^2[/tex].
Assim, a área da região colorida de azul é:
[tex]\qquad A_{\text{azul }}=A_1+A_2+A_3[/tex]
[tex]\qquad A_{\text{azul }}=26,46+13,23+13,23[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$A_{\text{azul }}=52,92 \text{ cm}^2$}[/tex] .
(b) Para justificar a afirmação de que o triângulo colorido de amarelo é isósceles, devemos garantir que dois dos lados desse triângulo têm o mesmo comprimento. Para facilitar, vamos denotar o triângulo colorido de amarelo por triângulo [tex]ABC.[/tex]
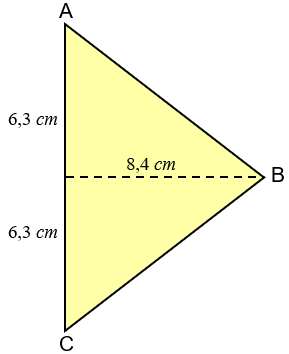
- Da figura ao lado, obtemos diretamente que o comprimento do lado [tex]\overline{AC}[/tex] é [tex]\boxed{12,6 \text{ cm}} \, .[/tex]
- Os lados [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex] têm o mesmo comprimento, já que ambos os segmentos são hipotenusas de triângulos retângulos de catetos com comprimentos [tex]6,3 \text{ cm} \, [/tex] e [tex]8,4 \text{ cm}.[/tex] Veja que, mesmo sem calcular esse comprimento, já podemos garantir que [tex]ABC[/tex] é um triângulo isósceles; mas vamos fazê-lo para verificarmos se o triângulo [tex]ABC[/tex] é apenas isósceles ou é equilátero. Seja, então, [tex]c[/tex] o comprimento dos segmentos [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex]. Do Teorema de Pitágoras, segue que:
[tex]\qquad \qquad c^2= 6,3^2+8,4^2[/tex]
[tex]\qquad \qquad c^2= 39,69+70,56[/tex]
[tex]\qquad \qquad c^2= 110,25[/tex]
[tex]\qquad \qquad c=\pm \sqrt{110,25}[/tex]
[tex]\qquad \qquad c=\pm 10,5.[/tex]
Como [tex]c[/tex] é um comprimento, temos que [tex]\boxed{c=10,5 \text{ cm}} \, [/tex] e com isso concluímos que [tex]ABC[/tex] é um triângulo isósceles, mas não equilátero.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
