✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Médio )
As retas [tex]r[/tex] e [tex]s[/tex] mostradas no plano cartesiano [tex]xOy [/tex] abaixo têm as seguintes equações gerais:
[tex] \qquad r: 2x+y-10=0, [/tex]
[tex]\qquad s: 2x+7y+14=0.[/tex]
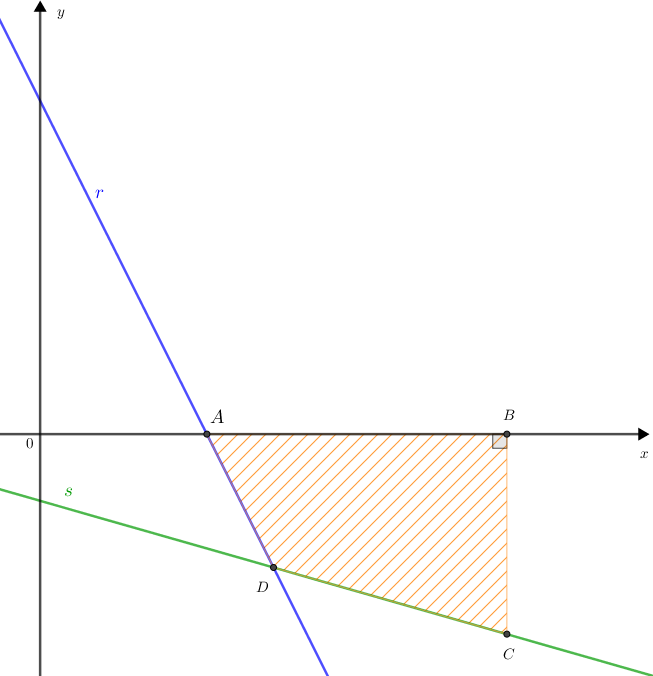
Sabendo que:
- [tex]A[/tex] e [tex]B[/tex] são pontos do eixo [tex]Ox[/tex];
- [tex]A[/tex] e [tex]D[/tex] são pontos de [tex]r[/tex];
- [tex]C[/tex] e [tex]D[/tex] são pontos de [tex]s[/tex];
- A distância do ponto [tex]B[/tex] à origem do sistema é [tex]14[/tex];
determinar a área do quadrilátero [tex]ABCD[/tex].
Solução
(1) Antes de mais nada, vamos determinar as coordenadas dos pontos [tex]A, \, B, \, C[/tex] e [tex]D[/tex] com relação ao plano cartesiano [tex]xOy [/tex] fixado. A princípio, essas coordenadas serão assim denotadas:
[tex]A=\left(x_A,y_A\right);\qquad B=\left(x_B,y_B\right);\qquad C=\left(x_C,y_C\right);\qquad D=\left(x_D,y_D\right).[/tex]
- Como [tex]A[/tex] e [tex]B[/tex] são pontos do eixo [tex]Ox[/tex], então [tex]y_A=y_B=0[/tex], ou seja: [tex]A=\left(x_A,0\right)[/tex] e [tex]B=\left(x_B,0\right)[/tex].
- A distância do ponto [tex]B[/tex] à origem do sistema é [tex]14[/tex]; logo, [tex]\boxed{B=\left(14,0\right)}[/tex].
- [tex]A=\left(x_A,0\right)[/tex] é ponto da reta [tex]r[/tex]; assim, as coordenadas de [tex]A[/tex] satisfazem a equação de [tex]r[/tex]:
- O segmento [tex]\overline{BC}[/tex] é perpendicular ao eixo [tex]Ox[/tex], donde [tex]x_B=x_C[/tex], ou seja, [tex]C=\left(14,y_C\right).[/tex] E como [tex]C[/tex] é ponto da reta [tex]s[/tex], suas coordenadas satisfazem a equação de [tex]s[/tex]:
- [tex]D=\left(x_D,y_D\right)[/tex] é ponto das retas [tex]r[/tex] e [tex]s[/tex]; assim, as coordenadas de [tex]D[/tex] satisfazem simultaneamente as equações de [tex]r[/tex] e de [tex]s[/tex]. Com isso
[tex]\qquad r: 2x+y-10=0[/tex]
[tex]\qquad 2x_A+0-10=0[/tex]
[tex]\qquad 2x_A=10[/tex]
[tex]\qquad x_A=5.[/tex]
Dessa forma, [tex]\boxed{A=\left(5,0\right)}.[/tex]
[tex]\qquad s: 2x+7y+14=0[/tex]
[tex]\qquad 2\times 14+7y_C+14=0[/tex]
[tex]\qquad 28+7y_C+14=0[/tex]
[tex]\qquad 7y_C=-42[/tex]
[tex]\qquad y_C=-6.[/tex]
Portanto, [tex]\boxed{C=\left(14,-6\right)}.[/tex]
[tex]\qquad 2x_D+y_D-10=0=2x_D+7y_D+14[/tex],
donde segue que:
[tex]\qquad \cancel{2x_D}+y_D-10= \cancel{2x_D}+7y_D+14.[/tex]
[tex]\qquad y_D-10= 7y_D+14.[/tex]
[tex]\qquad -6y_D= 24.[/tex]
[tex]\qquad y_D= -4.[/tex]
De [tex]2x_D+y_D-10=0[/tex] e [tex]y_D= -4[/tex], vem que:
[tex]\qquad 2x_D-4-10=0[/tex]
[tex]\qquad 2x_D=14[/tex]
[tex]\qquad x_D=7[/tex]
e, portanto, [tex]\boxed{D=\left(7,-4\right)}.[/tex]
(2) Para calcularmos a área do quadrilátero [tex]ABCD[/tex], podemos decompô-lo em figuras cujas áreas possam ser facilmente calculadas. A figura a seguir mostra uma dessas decomposições.
Observe que na figura já aparecem as coordenadas que calculamos no item anterior.
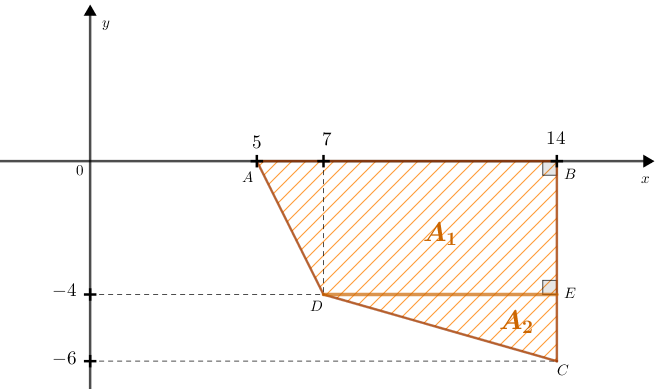
- A área [tex]A[/tex] do quadrilátero [tex]ABCD[/tex] pode ser particularmente decomposta como [tex]A=A_1+A_2[/tex], onde:
- [tex]A_1[/tex] é a área do trapézio retângulo [tex]ABED[/tex],
- [tex]A_2[/tex] é a área do triângulo retângulo [tex]DEC.[/tex]
Vamos aos cálculos das áreas [tex]A_1[/tex] e [tex]A_2[/tex].
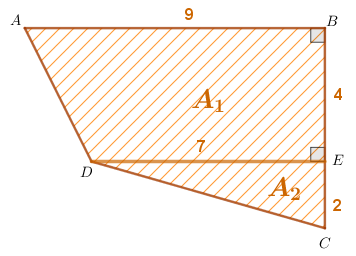
- [tex]A_1=\dfrac{\text{(base maior + base menor)} \times \text{altura}}{2}[/tex]
- [tex]A_2=\dfrac{\text{base } \times \text{altura}}{2}[/tex]
[tex]A_1=\dfrac{(9 + 7) \times 4}{2}[/tex]
[tex]A_1=32[/tex] unidades de área.
[tex]A_2=\dfrac{7 \times 2}{2}[/tex]
[tex]A_2=7[/tex] unidades de área.
Portanto, a área do quadrilátero [tex]ABCD[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$A=32+7=39$}[/tex] unidades de área.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
