✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
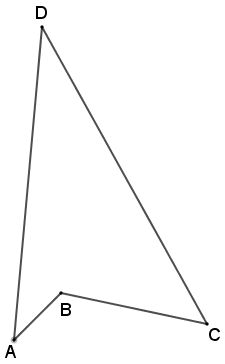
(OPM, 2014 – Adaptado) O quadrilátero [tex]ABCD[/tex] tem três ângulos internos iguais a [tex]45^{\circ}[/tex] nos vértices [tex]A[/tex], [tex]C[/tex] e [tex]D[/tex]. Se o segmento [tex]BD[/tex] mede [tex]8\text{ cm}[/tex], quanto mede a área de [tex]ABCD[/tex]?

Lembretes
(1) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
(2) A soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ[/tex].
(3) Se um triângulo possui dois ângulos com a mesma medida, então este triângulo é isósceles..
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
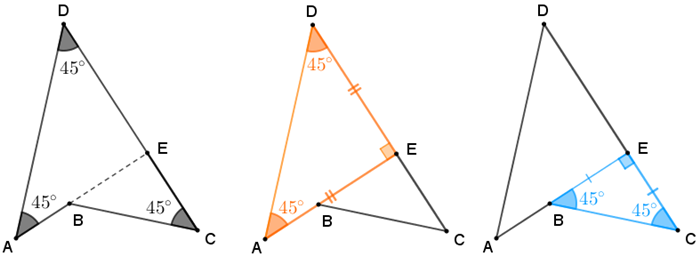
Seja [tex]E[/tex] o ponto de interseção do segmento [tex]\overline{CD}[/tex] com o prolongamento de [tex]\overline{AB}[/tex].
Observe que:
- Como os ângulos [tex]\hat A[/tex] e [tex]\hat D[/tex] medem [tex]45^{\circ}[/tex], o Lembrete (2) nos permite concluir que a medida do ângulo [tex]A\hat{B}D[/tex] é [tex]90^{\circ}[/tex] e, portanto, o triângulo [tex]AED[/tex] é retângulo. Mais do que isso, pelo Lembrete (3) [tex]AED[/tex] é um triângulo retângulo isósceles, com [tex]EA=ED[/tex]. Assim, a medida [tex]\textcolor{#FF6600}{S_1}[/tex] da área de [tex]AED[/tex] é dada por:
- Por outro lado, como o ângulo de vértice em [tex]E[/tex] é um ângulo reto e a medida do ângulo [tex]\hat C[/tex] é [tex]45^{\circ}[/tex], o Lembrete (2) nos garante que a medida do ângulo [tex]C\hat{B}E[/tex] é [tex]45^{\circ}[/tex]. Portanto, pelo Lembrete (3) , o triângulo [tex]BEC[/tex] é também um triângulo isósceles retângulo em [tex]E[/tex]. Com isso, [tex]EB=EC[/tex] e a medida [tex]\textcolor{#0099FF}{S_2}[/tex] da área de [tex]BEC[/tex] é dada por:
[tex]\qquad \textcolor{#FF6600}{S_1=\dfrac{EA\cdot ED}{2}=\dfrac{1}{2}ED^2}[/tex].
[tex]\qquad \textcolor{#0099FF}{S_2=\dfrac{EB\cdot EC}{2}=\dfrac{1}{2}EB^2}[/tex].
Note que a área do quadrilátero [tex]ABCD[/tex] é a soma das áreas dos triângulos [tex]AED[/tex] e [tex]BEC[/tex]; assim, se [tex]S[/tex] for a medida da área de [tex]ABCD[/tex], então:
[tex]\qquad S=\textcolor{#FF6600}{S_1}+\textcolor{#0099FF}{S_2}\\
\qquad S=\textcolor{#FF6600}{\dfrac{1}{2}ED^2}+\textcolor{#0099FF}{\dfrac{1}{2}EB^2}\\
\qquad S=\dfrac{1}{2}\left(ED^2+EB^2\right).\qquad \qquad \textcolor{#800000}{(i)}[/tex]
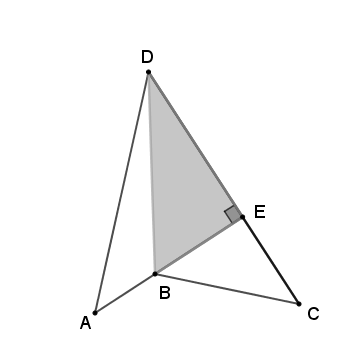 Mas lembre-se de que o ângulo de vértice em [tex]E[/tex] é retângulo; logo, podemos aplicar o Teorema de Pitágoras ao triângulo [tex]BED[/tex], já que o problema nos fornece [tex]BD=8\text{ cm} [/tex].
Mas lembre-se de que o ângulo de vértice em [tex]E[/tex] é retângulo; logo, podemos aplicar o Teorema de Pitágoras ao triângulo [tex]BED[/tex], já que o problema nos fornece [tex]BD=8\text{ cm} [/tex].
Assim, segue que:
[tex]\qquad ED^2+EB^2=BD^2[/tex]
[tex]\qquad ED^2+EB^2=8^2[/tex]
[tex]\qquad ED^2+EB^2=64.\qquad \qquad \textcolor{#800000}{(ii)}[/tex]
Substituindo [tex] \textcolor{#800000}{(ii)}[/tex] em [tex] \textcolor{#800000}{(i)}[/tex], obtemos
[tex]\qquad S=\dfrac{1}{2}\cdot 64[/tex]
[tex]\qquad S=32.[/tex]
Portanto, a medida da área do quadrilátero [tex]ABCD[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$\, 32\text{ cm}^2\,$}[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
