✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
(XXVIII OPM – 2009) Na figura abaixo, os triângulos [tex]ABC[/tex] e [tex]DEF[/tex] são equiláteros e os segmentos [tex]AD [/tex] e [tex]CE[/tex] medem respectivamente [tex]1\; [/tex]cm e [tex]2\; [/tex]cm.
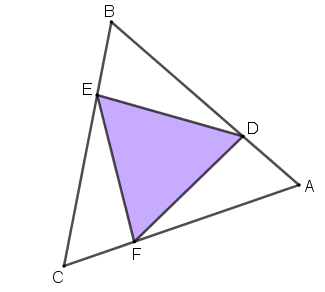
Determinar a medida da área do triângulo [tex]DEF.[/tex]

Lembretes para a Solução
(1) A medida de cada ângulo interno de um triângulo equilátero é [tex]60^\circ[/tex].
(2) A soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ[/tex].
(3) Se dois triângulos têm ordenadamente congruentes dois ângulos e o lado compreendido por eles, então estes triângulos são congruentes pelo caso A.L.A. .
(4) Se dois lados de um triângulo são proporcionais a dois lados de outro triângulo e os ângulos internos definidos por esses lados são congruentes, então os triângulos são semelhantes pelo caso L.A.L. .
(5) A área [tex] A_{teq}[/tex] de um triângulo equilátero de lados com comprimento [tex]l[/tex] pode ser assim calculada:
[tex]\qquad A_{teq}=\dfrac{l^2\cdot\sqrt{3}}{4}.[/tex]
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY.[/tex]
Solução 1
Muitos triângulos e poucas medidas de lados!
Isso aponta para utilização de semelhança ou congruência de triângulos. Vamos então investigar algumas medidas de ângulos. Para isso, vamos denotar por [tex]\textcolor{red}{\theta}[/tex] a medida em graus do ângulo [tex]C\hat{E}F[/tex].
- Observe que, como o triângulo [tex]ABC[/tex] é equilátero, então a medida do ângulo [tex]A\hat{C}B[/tex] é [tex] 60^\circ[/tex]. Como a soma dos ângulos internos de qualquer triângulo vale [tex]180^\circ[/tex], consequentemente, a medida do ângulo [tex]E\hat{F}C[/tex] é [tex] \textcolor{#009900}{180^\circ-60^\circ-\theta=\boxed{120^\circ-\theta}}.[/tex]
- Por outro lado, veja que a soma das medidas dos ângulos [tex]E\hat{F}C[/tex], [tex]E\hat{F}D[/tex] e [tex]D\hat{F}A[/tex] é [tex] 180^\circ[/tex] e o triângulo [tex]EFD[/tex] é equilátero. Assim, a medida de [tex]D\hat{F}A[/tex] é [tex] \textcolor{red}{180^\circ-(120^\circ-\theta)-60^\circ=\boxed{\theta}}[/tex] e, consequentemente, a medida do ângulo [tex]A\hat{D}F[/tex] é [tex] \textcolor{#009900}{180^\circ-\theta-60^\circ=\boxed{120^\circ-\theta}}.[/tex]
- Também podemos notar que a soma das medidas dos ângulos [tex]A\hat{D}F[/tex], [tex]F\hat{D}E[/tex] e [tex]E\hat{D}B[/tex] é [tex] 180^\circ.[/tex] Como o triângulo [tex]EFD[/tex] é equilátero, segue que a medida de [tex]E\hat{D}B[/tex] é [tex] \textcolor{red}{180^\circ-(120^\circ-\theta)-60^\circ=\boxed{\theta}}[/tex] e, então, a medida do ângulo [tex]B\hat{E}D[/tex] é [tex] \textcolor{#009900}{180^\circ-\theta-60^\circ=\boxed{120^\circ-\theta}}.[/tex]
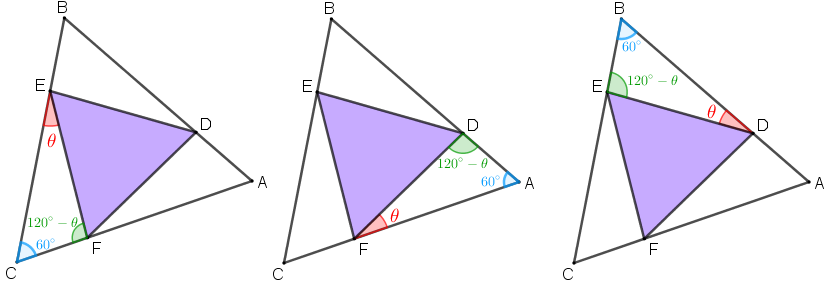
Dessa forma, pelo caso A.L.A., os triângulos [tex]EFC[/tex], [tex]FDA[/tex] e [tex]DEB[/tex] são congruentes e, portanto, seus lados correspondentes têm a mesma medida.
Como [tex]AD=1\; [/tex]cm e [tex]CE=2\; [/tex]cm , temos que [tex]AD=BE=CF=1\; [/tex]cm e [tex]CE=BD=AF=2\; [/tex]cm.
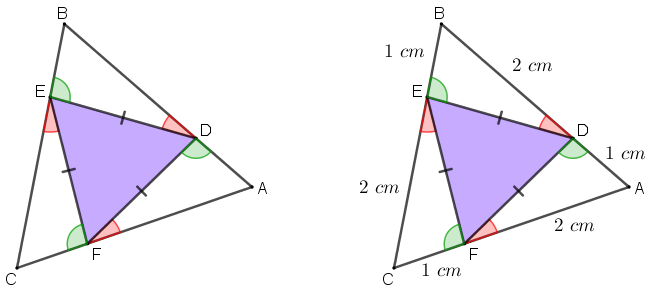
Agora, vamos tentar obter a medida dos lados do triângulo [tex]DEF[/tex] utilizando o triângulo [tex]ABC[/tex].
No triângulo [tex]ABC[/tex] consideraremos a altura [tex]\overline{BH}[/tex] relativa ao lado [tex]\overline{CA}[/tex]. Como [tex]ABC[/tex] é triângulo retângulo, [tex]\overline{BH}[/tex] também é uma mediana; logo [tex]CH=\dfrac{3}{2}\; [/tex]cm.
A partir dessa informação, ao observarmos com cuidado os triângulos [tex]BCH[/tex] e [tex]ECF[/tex] podemos concluir que eles são semelhantes, já que os lados [tex]\overline{CH}[/tex] e [tex]\overline{CB}[/tex] são proporcionais aos lados [tex]\overline{CF}[/tex] e [tex]\overline{CE}[/tex], além de esses lados definirem, respectivamente, dois ângulos de [tex]60^\circ:[/tex]
[tex]\qquad \qquad \dfrac{CH}{CB}=\dfrac{\frac{3}{2}}{3}=\dfrac{3}{2} \times \dfrac{1}{3}= \dfrac{1}{2}=\dfrac{CF}{CE}.[/tex]
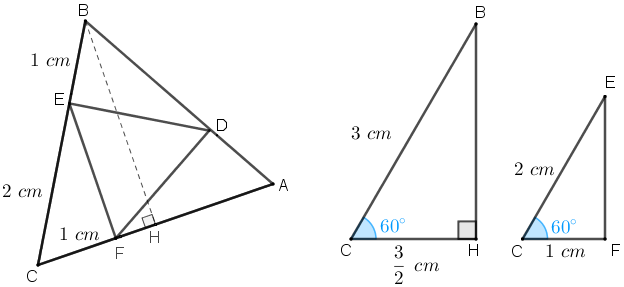
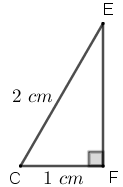
Dessa semelhança de triângulos, concluímos que [tex]E\hat{F}C[/tex] é um ângulo de [tex]90^\circ[/tex] e, portanto, [tex]ECF[/tex] é um triângulo retângulo. Com isso, podemos obter a medida do segmento [tex]\overline{EF}[/tex] aplicando o Teorema de Pitágoras no triângulo [tex]CFE:[/tex]
[tex]\qquad EF^2+1^2=2^2\\
\qquad EF^2=4-1=3\\
\qquad EF=\pm\sqrt{3}.[/tex]
Como [tex]EF \gt 0[/tex], temos que [tex] \boxed{EF=\sqrt{3}\; \text{ cm}}.[/tex]
Pronto, finalmente temos condições de calcular a medida [tex]S[/tex] da área do triângulo [tex]DEF.[/tex]
Pela fórmula do Lembrete (5), temos que:
[tex]\qquad S=\dfrac{\left(\sqrt{3}\right)^2\cdot\sqrt{3}}{4}\\
\qquad \fcolorbox{black}{#eee0e5}{$S=\dfrac{3\sqrt{3}}{4}\; \text{ cm}^2$}\; .[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembretes para a Solução 2
 ✐ Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a,\; b,\; h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
✐ Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a,\; b,\; h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Chamamos cosseno de [tex]\theta[/tex], e denotamos por [tex]cos\; \theta[/tex], a razão entre os comprimentos do cateto adjacente a [tex]\theta[/tex] e da hipotenusa:[tex]\boxed{ cos\; \theta= \dfrac{b}{h}}.[/tex]
Chamamos seno de [tex]\theta[/tex], e denotamos por [tex]sen\; \theta[/tex], a razão entre os comprimentos do cateto oposto a [tex]\theta[/tex] e da hipotenusa:[tex]\boxed{ sen\; \theta= \dfrac{a}{h}}.[/tex]
 ✐ [tex]\; \; sen\; 60^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad[/tex] [tex] cos\; 60^{\circ}=\dfrac{1}{2}\; .[/tex]
✐ [tex]\; \; sen\; 60^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad[/tex] [tex] cos\; 60^{\circ}=\dfrac{1}{2}\; .[/tex]
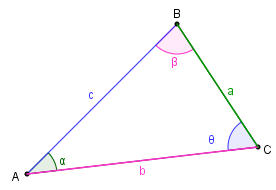
✐ Lei dos cossenos:
Para um triângulo [tex]ABC[/tex] da figura ao lado, a lei dos cossenos garante as seguintes relações entre seus lados e seus ângulos:
[tex]\qquad a^2 = b^2 + c^2 – 2\cdot b\cdot c\cdot cos\; \alpha[/tex];
[tex]\qquad b^2 = a^2 + c^2 – 2\cdot a\cdot c\cdot cos\; β[/tex];
[tex]\qquad c^2 = a^2 + b^2 – 2\cdot a\cdot b\cdot cos\; \theta [/tex].
Solução 2
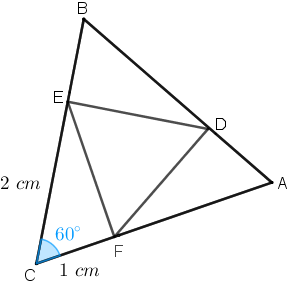
A partir da determinação dos comprimentos [tex]AD=BE=CF=1\; [/tex]cm e [tex]CE=BD=AF=2\; [/tex]cm, podemos utilizar a Lei dos cossenos no triângulo [tex]CFE[/tex] para obter rapidamente o comprimento do segmento [tex]\overline{EF}:[/tex]
[tex]\quad EF^2=1^2+2^2-2\cdot 1\cdot 2 \cdot cos\; 60^\circ[/tex]
[tex]\quad EF^2=1+4-4 \cdot \dfrac{1}{2}[/tex]
[tex]\quad EF^2=3[/tex]
[tex]\quad EF=\pm\sqrt{3}.[/tex]
Como [tex]EF \gt 0[/tex], temos que [tex] \boxed{EF=\sqrt{3}\;\text{ cm} }[/tex].
Vamos finalizar esta solução utilizando a definição de seno de um ângulo para calcular o comprimento [tex]h[/tex] da altura do triângulo [tex]EFD[/tex] e, consequentemente, a medida [tex]S[/tex] de sua área.
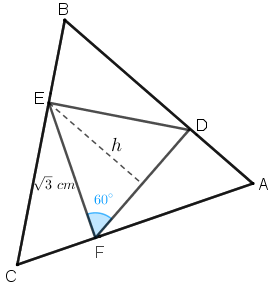
- [tex] sen\; 60^\circ=\dfrac{h}{\sqrt{3}}[/tex]
- [tex]S=\dfrac{base \times altura}{2}[/tex]
[tex] \dfrac{\sqrt{3}}{2}=\dfrac{h}{\sqrt{3}}[/tex]
[tex] h= \dfrac{3}{2}\; \text{ cm}.\\
\; [/tex]
[tex]S=\dfrac{\sqrt{3}\times \frac{3}{2}}{2}[/tex]
[tex] \fcolorbox{black}{#eee0e5}{$S=\dfrac{3\sqrt{3}}{4}\; \text{ cm}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 3

A partir da determinação dos comprimentos [tex]AD=BE=CF=1\; \text{ cm}[/tex] e [tex]CE=BD=AF=2\; \text{ cm}[/tex], podemos utilizar a Lei dos cossenos no triângulo [tex]CFE[/tex] para obter rapidamente o comprimento do segmento [tex]\overline{EF}:[/tex]
[tex]\quad EF^2=1^2+2^2-2\cdot 1\cdot 2 \cdot cos\; 60^\circ[/tex]
[tex]\quad EF^2=1+4-4 \cdot \dfrac{1}{2}[/tex]
[tex]\quad EF^2=3[/tex]
[tex]\quad EF=\pm\sqrt{3}.[/tex]
Como [tex]EF \gt 0[/tex], temos que [tex] \boxed{EF=\sqrt{3}\; \text{ cm}}.[/tex]
Utilizando a fórmula do Lembrete (5), temos que:
[tex]\qquad S=\dfrac{l^2\cdot\sqrt{3}}{4}\\
\qquad S=\dfrac{\left(\sqrt{3}\right)^2\cdot\sqrt{3}}{4}\\
\qquad \fcolorbox{black}{#eee0e5}{$S=\dfrac{3\sqrt{3}}{4}\; \text{ cm}^2$}\; .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
