✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
[tex]ABCD[/tex] é um trapézio. Determinar as medidas dos ângulos internos [tex]\hat{B}[/tex] e [tex]\hat{D}[/tex].
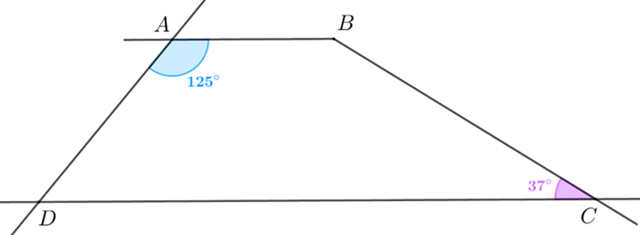

Lembretes
(1) Ângulos correspondentes definidos por duas retas paralelas e uma reta transversal são congruentes. (Se você não se lembra do assunto, não deixe de dar uma passadinha nesta Sala para Leitura.)
(2) A soma dos ângulos internos de um polígono convexo de [tex]n[/tex] lados ([tex]n\gt 2[/tex]) é dada por:
[tex]\qquad \qquad \boxed{S_{i_n}=\left(n-2\right)\cdot 180^\circ}.[/tex]
Solução
Como [tex]ABCD[/tex] é um trapézio, ele possui dois lados opostos paralelos (suas bases). Observe que, se prolongarmos os segmentos [tex]AD[/tex] e [tex]BC[/tex], esses prolongamentos se intersectarão; logo, não são [tex]AD[/tex] e [tex]BC[/tex] os lados opostos paralelos.
Assim, [tex]AB[/tex] e [tex]DC[/tex] são duas retas paralelas intersectadas pela transversal [tex]BC[/tex]. Com isso, os ângulos com vértices [tex]B[/tex] e [tex]C[/tex] e com medidas [tex]x[/tex] e [tex]37^\circ[/tex] são correspondentes e, portanto, [tex]x=37^\circ[/tex], segundo o Lembrete (1).
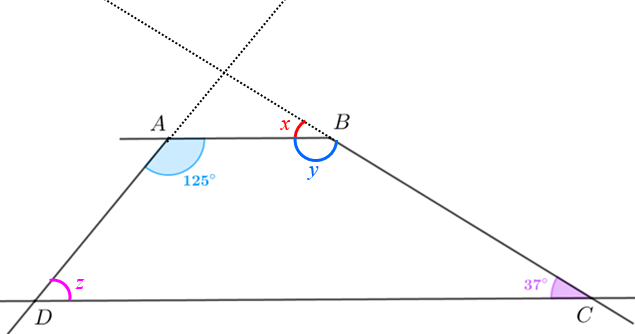
Por outro lado, observando novamente o vértice [tex]B[/tex], vemos que os ângulos de medida [tex]x[/tex] e [tex]y[/tex] são ângulos suplementares, ou seja, [tex]x+y=180^\circ[/tex]; donde concluímos que [tex]y=180^\circ-37^\circ=\boxed{\textcolor{#345af9}{143^\circ}}[/tex] .
Finalmente, pelo Lembrete (2), a soma dos ângulos internos do trapézio [tex]ABCD[/tex] é
[tex]\qquad S_{i_4}=\left(4-2\right)\cdot 180^\circ=360^\circ[/tex];
logo, a medida [tex]z[/tex] do ângulo [tex]\hat{D}[/tex] é
[tex]\qquad z=360^\circ-125^\circ-143^\circ-37^\circ= \, \boxed{\textcolor{#FF00FF}{55^\circ}} \, .[/tex]
Pelo exposto, as medidas dos ângulos internos [tex]\hat{B}[/tex] e [tex]\hat{D}[/tex] são, respectivamente, [tex] \, \fcolorbox{black}{#eee0e5}{$143^\circ \text{ e } 55^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
