✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
Quantas soluções com quatro inteiros ímpares tem a equação
[tex]\qquad \qquad \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}=1\;[/tex]?
AJUDA
Em várias situações é possível determinarmos a paridade de expressões envolvendo números inteiros, a partir da paridade desses números, sem sequer calcular as expressões.
O que nos permite "adivinhar” a paridade de algumas expressões desse tipo são estas três propriedades;
(1) A soma de dois números inteiros de mesma paridade é par.
(2) A soma de dois números inteiros de paridade oposta é ímpar.
(3) O produto de dois números inteiros só será ímpar se os dois números forem ímpares.
Com elas, podemos construir as tabelinhas abaixo.
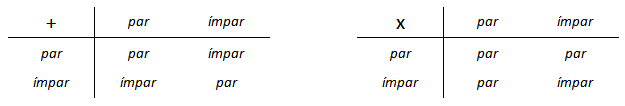
Solução
Vamos supor que [tex]m,\,n,\,x,\,y[/tex] sejam inteiros ímpares tais que [tex]\boxed{\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{x}+\dfrac{1}{y}=1}\,.[/tex]
Assim, segue que:
[tex]\qquad \dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{x}+\dfrac{1}{y}=1\\
\qquad \dfrac{nxy+mxy+mny+mnx}{mnxy}=1\\\
\qquad nxy+mxy+mny+mnx=mnxy\,.\qquad \textcolor{#800000}{(i)}\\[/tex]
Como [tex]m,\,n,\,x,\,y[/tex] são ímpares, a propriedade (3) da Ajuda nos garante que cada parcela da adição que aparece na expressão [tex]\textcolor{#800000}{(i)}[/tex] é um número ímpar. Assim, como "a soma de dois inteiros ímpares é um inteiro par" e "a soma de dois inteiros pares é par", então
► a soma que aparece no lado esquerdo da igualdade de [tex]\textcolor{#800000}{(i)}[/tex] é um número par.
[tex]\underbrace{\underbrace{nxy+mxy}_{\textcolor{red}{par}}+\underbrace{mny+mnx}_{\textcolor{red}{par}}}_{\textcolor{red}{par}}[/tex]
Por outro lado, como [tex]m,\,n,\,x,\,y[/tex] são ímpares, a mesma propriedade (3) da Ajuda nos garante que
► o produto que aparece no lado direito da igualdade de [tex]\textcolor{#800000}{(i)}[/tex] é um número ímpar.
[tex]\underbrace{mnxy}_{\textcolor{#38ACEC}{ímpar}}[/tex]
Mas isso é impossível de acontecer, pois sabemos que não existe um número inteiro que seja simultaneamente par e ímpar!
[tex]\qquad \underbrace {nxy+mxy+mny+mnx}_{\textcolor{red}{\text{número par}}}=\underbrace{mnxy}_{\textcolor{#38ACEC}{\text{número ímpar}}}[/tex]
Com isso, concluímos que não existem inteiros ímpares [tex]m,\,n,\,x,\,y[/tex] tais que [tex]\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{x}+\dfrac{1}{y}=1\;[/tex] e, portanto, a equação do problema não tem solução com quatro inteiros ímpares.
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |