✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Muito Difícil)
Ali Babão apresentou aos seus discípulos um tipo interessante de equações polinomiais:
- equações cujos coeficientes equidistantes dos extremos ou são todos iguais ou são todos simétricos.
Esquematicamente, são equações da forma
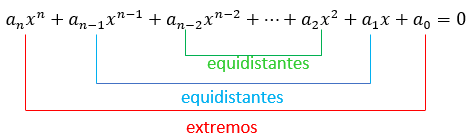
tais que ou
[tex]\qquad \qquad a_n=a_0\,,\, a_{n-1}=a_1\,,\, a_{n-2}=a_2,\cdots\, [/tex]
ou
[tex]\qquad \qquad a_n=-a_0\,,\,a_{n-1}=-a_1\,,\, a_{n-2}=-a_2,\cdots\, [/tex] .
Ajude os discípulos do mestre Ali, respondendo os itens abaixo.
(a) Se os coeficientes equidistantes dos extremos de uma equação são simétricos, então essa equação admite a raiz [tex]1[/tex]?
(b) Se os coeficientes equidistantes dos extremos de uma equação forem iguais, essa equação admite a raiz [tex]-1[/tex]?
(c) Resolva a equação [tex]6x^3-19x^2+19x-6=0[/tex].

AJUDA
✏ Destrinchando as caracterizações
Para visualizar melhor as duas caracterizações de equações dadas no problema, escreva ordenadamente os coeficientes da equação a ser analisada em duas linhas:
- em uma linha, escreva do de maior índice para o de menor índice (inclusive os coeficientes iguais a [tex]0[/tex]);
- na outra linha, escreva do de menor índice para o de maior índice (inclusive os coeficientes iguais a [tex]0[/tex]).
[tex]\begin{array}{c|c|c|c|c|c|c}
a_n&a_{n-1}&a_{n-2}&\cdots&a_2&a_1&a_0\\
a_0&a_1&a_2&\cdots&a_{n-2}&a_{n-1}&a_n\\
\end{array}[/tex]
►Uma equação ter coeficientes equidistantes dos extremos simétricos equivale a dizer que em todas as [tex]n+1[/tex] colunas do respectivo esqueminha os elementos são simétricos um do outro.
Uma observação importante é sobre o(s) coeficiente(s) central(ais):
[tex]\begin{array}{c|c|c|c|c|c|c|c|c}
a_n&a_{n-1}&a_{n-2}&\cdots&\textcolor{red}{a_{\frac{n}{2}}}&\cdots&a_2&a_1&a_0\\
a_0&a_1&a_2&\cdots&\textcolor{red}{a_{\frac{n}{2}}}&\cdots&a_{n-2}&a_{n-1}&a_n\\
\end{array}[/tex]
►Se o grau da equação é ímpar, então essa equação tem um número par de coeficientes; logo, existem dois coeficientes centrais: os coeficientes [tex]\textcolor{red}{a_{\frac{n-1}{2}}}[/tex] e [tex]\textcolor{red}{a_{\frac{n+1}{2}}}[/tex].
[tex]\begin{array}{c|c|c|c|c|c|c|c|c|c}
a_n&a_{n-1}&a_{n-2}&\cdots&\textcolor{red}{a_{\frac{n+1}{2}}}&\textcolor{red}{a_{\frac{n-1}{2}}}&\cdots&a_2&a_1&a_0\\
a_0&a_1&a_2&\cdots&\textcolor{red}{a_{\frac{n-1}{2}}}&\textcolor{red}{a_{\frac{n+1}{2}}}&\cdots&a_{n-2}&a_{n-1}&a_n\\
\end{array}[/tex]
Equações polinomiais desse tipo são o que a Matemática denomina como equações recíprocas.
Solução
(a) Considere uma equação polinomial
[tex]\qquad \qquad P(x)= a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_2x^2+a_1x+a_0=0[/tex]
cujos coeficientes equidistantes dos extremos sejam simétricos.
Assim,
[tex]\qquad \qquad a_n=-a_0\,,\,a_{n-1}=-a_1\,,\, a_{n-2}=-a_2,\cdots\, [/tex].
Veja o esqueminha geral:
[tex]\begin{array}{c|c|c|c|c|c|c}
a_n=-a_0&a_{n-1}=-a_{1}&a_{n-2}=-a_{2}&\cdots&a_2&a_1&a_0\\
a_0&a_1&a_2&\cdots&a_{n-2}=-a_{2}&a_{n-1}=-a_{1}&a_n=-a_0\
\end{array}[/tex]
Vamos dividir a nossa discussão em função da paridade do grau da equação e utilizar os esqueminhas que destacam o termo central para facilitar o entendimento desta solução.
O que devemos avaliar em cada caso é se a equação [tex] P(x)=0[/tex] admite ou não a raiz [tex]1[/tex], isto é, se [tex] P(1)=0[/tex] ou [tex] P(1)\ne 0[/tex].
(1) Suponha que o grau da nossa equação seja ímpar.
Neste caso, o esqueminha fica assim:
[tex]\begin{array}{c|c|c|c|c|c|c|c}
a_n=-a_0&a_{n-1}=-a_{1}&\cdots&a_{\frac{n+1}{2}}=-a_{\frac{n-1}{2}}&a_{\frac{n-1}{2}}&\cdots&a_1&a_0\\
a_0&a_1&\cdots&a_{\frac{n-1}{2}}&a_{\frac{n+1}{2}}=-a_{\frac{n-1}{2}}&\cdots&a_{n-1}=-a_{1}&a_n=-a_0\\
\end{array}[/tex]
e
[tex]\qquad P(1)=a_n\cdot 1^n+a_{n-1}\cdot 1^{n-1}+a_{n-2}\cdot 1^{n-2}+\cdots\\
\qquad \qquad \quad \cdots +a_{\frac{n+1}{2}}\cdot 1^{\frac{n+1}{2}}+a_{\frac{n-1}{2}}\cdot 1^{\frac{n-1}{2}}+\cdots+a_2\cdot 1^2+a_1\cdot 1+a_0[/tex]
[tex]\qquad P(1)=a_n+a_{n-1}+a_{n-2}+\cdots+a_{\frac{n+1}{2}}+a_{\frac{n-1}{2}}+\cdots+a_2+a_1+a_0[/tex]
[tex]\qquad P(1)=-a_0-a_{1}-a_{2}+\cdots-a_{\frac{n-1}{2}}+a_{\frac{n-1}{2}}+\cdots+a_1+a_0[/tex]
[tex]\qquad P(1)=-\textcolor{red}{\cancel{a_0}}-\textcolor{blue}{\cancel{a_{1}}}-\textcolor{#B9418E}{\cancel{a_{2}}}+\cdots-\textcolor{green}{\cancel{a_{\frac{n-1}{2}}}}+\textcolor{green}{\cancel{a_{\frac{n-1}{2}}}}+\cdots+\textcolor{#B9418E}{\cancel{a_{2}}}+\textcolor{blue}{\cancel{a_{1}}}+\textcolor{red}{\cancel{a_0}}[/tex]
[tex]\qquad P(1)=0[/tex].
(2) Suponha que o grau da nossa equação seja par.
Agora, o esqueminha fica assim:
[tex]\begin{array}{c|c|c|c|c|c|c}
a_n=-a_0&a_{n-1}=-a_{1}&\cdots&\textcolor{#FF00FF}{a_{\frac{n}{2}}=-a_{\frac{n}{2}}}&\cdots&a_1&a_0\\
a_0&a_1&\cdots&\textcolor{#FF00FF}{a_{\frac{n}{2}}}&\cdots&a_{n-1}=-a_{1}&a_n=-a_0\\
\end{array}[/tex]
Antes de fazermos o cálculo de [tex]P(1)[/tex], observe que para termos elementos simétricos na coluna relativa ao termo central, [tex]a_{\frac{n}{2}}=0[/tex]. pois [tex]0[/tex] é o único número cujo simétrico é ele próprio.
Vamos aos cálculos!
[tex]\qquad P(1)=a_n\cdot 1^n+a_{n-1}\cdot 1^{n-1}+a_{n-2}\cdot 1^{n-2}+\cdots\\
\qquad \qquad \quad \cdots +a_{\frac{n}{2}}\cdot 1^{\frac{n}{2}}+\cdots+a_2\cdot 1^2+a_1\cdot 1+a_0[/tex]
[tex]\qquad P(1)=a_n+a_{n-1}+a_{n-2}+\cdots+0+\cdots+a_2+a_1+a_0[/tex]
[tex]\qquad P(1)=-a_0-a_{1}-a_{2}+\cdots+0+\cdots+a_2+a_1+a_0[/tex]
[tex]\qquad P(1)=-\textcolor{red}{\cancel{a_0}}-\textcolor{blue}{\cancel{a_{1}}}-\textcolor{#B9418E}{\cancel{a_{2}}}+\cdots+0+\cdots+\textcolor{#B9418E}{\cancel{a_{2}}}+\textcolor{blue}{\cancel{a_{1}}}+\textcolor{red}{\cancel{a_0}}[/tex]
[tex]\qquad P(1)=0[/tex].
Por (1) e (2), concluímos que [tex]P(1)=0[/tex].
Assim,
[tex]1[/tex] é, de fato, raiz de qualquer equação polinomial cujos coeficientes equidistantes dos extremos são simétricos.
(b) Considere, agora, uma equação polinomial
[tex]\qquad \qquad P(x)= a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_2x^2+a_1x+a_0=0[/tex]
cujos coeficientes equidistantes dos extremos sejam iguais.
Assim,
[tex]\qquad \qquad a_n=a_0\,,\,a_{n-1}=a_1\,,\, a_{n-2}=a_2,\cdots\, [/tex].
Veja o esqueminha geral:
[tex]\begin{array}{c|c|c|c|c|c|c}
a_n=a_0&a_{n-1}=a_{1}&a_{n-2}&\cdots&a_2&a_1&a_0\\
a_0&a_1&a_2&\cdots&a_{n-2}=a_{2}&a_{n-1}=a_{1}&a_n=a_0\
\end{array}[/tex]
O que vamos avaliar neste item é se a equação [tex] P(x)=0[/tex] admite ou não a raiz [tex]-1[/tex], isto é, se [tex] P(-1)=0[/tex] ou [tex] P(-1)\ne 0[/tex].
Aqui parece que teremos problemas, já que, diferentemente do item anterior no qual tínhamos potências com base [tex]1[/tex], as potências com base [tex]-1[/tex] apresentam dois valores: [tex]1[/tex] ou [tex]-1\,.[/tex]
Vamos dividir, mais uma vez, a nossa discussão em função da paridade do grau da equação e também utilizar os esqueminhas que destacam o termo central.
(1) Aqui, vamos supor inicialmente que o grau da nossa equação seja par.
Então, o nosso esqueminha fica assim:
[tex]\begin{array}{c|c|c|c|c|c|c}
a_n=a_0&a_{n-1}=a_{1}&\cdots&\textcolor{#FF00FF}{a_{\frac{n}{2}}}&\cdots&a_1&a_0\\
a_0&a_1&\cdots&\textcolor{#FF00FF}{a_{\frac{n}{2}}}&\cdots&a_{n-1}=a_{1}&a_n=a_0\\
\end{array}[/tex]
Note que:
[tex]\qquad P(-1)=a_n\cdot \left(-1\right)^n+a_{n-1}\cdot \left(-1\right)^{n-1}+a_{n-2}\cdot \left(-1\right)^{n-2}+\cdots\\
\qquad \qquad \cdots +a_{\frac{n}{2}}\cdot \left(-1\right)^{\frac{n}{2}}+\cdots+a_2\cdot \left(-1\right)^2+a_1\cdot \left(-1\right)+a_0[/tex]
e como [tex]n[/tex] é par, temos que:
[tex]\qquad P(-1)=a_n-a_{n-1}+a_{n-2}+\cdots+a_{\frac{n}{2}}\cdot \left(-1\right)^{\frac{n}{2}}+\cdots+a_2-a_1+a_0[/tex]
[tex]\qquad P(-1)=a_0-a_{1}+a_{2}+\cdots+a_{\frac{n}{2}}\cdot \left(-1\right)^{\frac{n}{2}}+\cdots+a_2-a_1+a_0[/tex]
[tex]\qquad P(-1)=2a_0-2a_{1}+2a_{2}+\cdots+a_{\frac{n}{2}}\cdot \left(-1\right)^{\frac{n}{2}}[/tex].
Perceba que não temos como garantir se [tex] \left(-1\right)^{\frac{n}{2}}[/tex] é [tex]1[/tex] ou [tex]-1[/tex] e muito menos avaliar a soma [tex]2a_0-2a_{1}+2a_{2}+\cdots+a_{\frac{n}{2}}\cdot \left(-1\right)^{\frac{n}{2}}[/tex] sem conhecermos os coeficientes da equação.
Por exemplo, a equação polinomial [tex]P(x)=x^2+2x+1=0[/tex] tem coeficientes equidistantes dos extremos iguais, tem grau par e [tex]P(-1)=0[/tex].
Já a equação [tex]P(x)=x^4+x^3+x^2+x+1=0[/tex] tem coeficientes equidistantes dos extremos iguais, tem grau par, mas [tex]P(-1)=1[/tex].
Veja que a equação [tex]P(x)=x^4+x^3+ax^2+x+1[/tex] tem coeficientes equidistantes dos extremos iguais, tem grau par, mas [tex]P(-1)=a[/tex], para qualquer [tex]a \in \mathbb{R}[/tex], o que reforça que este caso que estamos analisando apresenta equações polinomiais [tex]P(x)=0[/tex] cujo valor [tex]P(-1)[/tex] depende dos seus coeficientes.
Dessa forma,
Não podemos garantir que [tex]-1[/tex] seja raiz de qualquer equação polinomial de grau par, cujos coeficientes equidistantes dos extremos são iguais.
(2) Vamos supor, agora, que o grau da nossa equação seja ímpar.
Neste caso, o esqueminha fica assim:
[tex]\begin{array}{c|c|c|c|c|c|c|c}
a_n=a_0&a_{n-1}=a_{1}&\cdots&a_{\frac{n+1}{2}}=a_{\frac{n-1}{2}}&a_{\frac{n-1}{2}}&\cdots&a_1&a_0\\
a_0&a_1&\cdots&a_{\frac{n-1}{2}}&a_{\frac{n+1}{2}}=a_{\frac{n-1}{2}}&\cdots&a_{n-1}=a_{1}&a_n=a_0\\
\end{array}[/tex]
e
[tex]\;P(-1)=a_n\cdot \left(-1\right)^n+a_{n-1}\cdot \left(-1\right)^{n-1}+a_{n-2}\cdot \left(-1\right)^{n-2}+\cdots+a_{\frac{n+1}{2}}\cdot \left(-1\right)^{\frac{n+1}{2}}+\\
\qquad \qquad \quad +a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n-1}{2}}+\cdots+a_2\cdot \left(-1\right)^2+a_1\cdot \left(-1\right)+a_0\,.[/tex]
Como aqui [tex]n[/tex] é ímpar,
[tex]\quad P(-1)=-a_n+a_{n-1}-a_{n-2}+\cdots\\
\quad \qquad \quad +a_{\frac{n+1}{2}}\cdot \left(-1\right)^{\frac{n+1}{2}}+a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n-1}{2}}+\cdots +a_2-a_1+a_0[/tex]
[tex]\quad P(-1)=-a_0+a_{1}-a_{2}+\cdots+a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n+1}{2}}+a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n-1}{2}}+\cdots\\
\quad \qquad \quad cdots +a_2-a_1+a_0[/tex]
[tex]\quad P(-1)=-\textcolor{red}{\cancel{a_0}}+\textcolor{blue}{\cancel{a_{1}}}-\textcolor{#B9418E}{\cancel{a_{2}}}+\cdots+a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n+1}{2}}+a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n-1}{2}}+\cdots\\
\qquad \qquad \quad cdots+\textcolor{#B9418E}{\cancel{a_{2}}}-\textcolor{blue}{\cancel{a_{1}}}+\textcolor{red}{\cancel{a_0}}[/tex]
[tex]\quad P(-1)=a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n+1}{2}}+a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n-1}{2}}\\
\,\,[/tex].
Por fim, veja que [tex]\dfrac{n-1}{2}+1=\dfrac{n+1}{2}[/tex]; assim, os expoentes [tex]\dfrac{n-1}{2}[/tex] e [tex]\dfrac{n+1}{2}[/tex] do [tex]-1[/tex] são números consecutivos. Logo, uma das potências [tex]\left(-1\right)^\frac{n-1}{2}[/tex] ou [tex]\left(-1\right)^\frac{n+1}{2}[/tex] é [tex]1[/tex] e a outra é [tex]-1[/tex] e, com isso,
[tex]\qquad P(-1)=a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n+1}{2}}+a_{\frac{n-1}{2}}\cdot \left(-1\right)^{\frac{n-1}{2}}=0\,\,[/tex].
Portanto, podemos concluir que
[tex]-1[/tex] é raiz de qualquer equação polinomial de grau ímpar cujos coeficientes equidistantes dos extremos são iguais.
(c) Resolva a equação [tex]6x^3-19x^2+19x-6=0[/tex]
Observe que [tex]6x^3-19x^2+19x-6=0[/tex] é uma equação polinomial cujos coeficientes equidistantes dos extremos são simétricos; assim, [tex]1[/tex] é uma de suas raízes. Vamos, então, fazer a divisão da expressão [tex]6x^3-19x^2+19x-6[/tex] por [tex]x-1[/tex]:
| [tex]\;\;6x^3-19x^2+19x-6[/tex] | [tex]x-1[/tex] | |
| [tex]\textcolor{red}{-6x^3+6x^2}[/tex] | [tex]\textcolor{red}{6x^2}\textcolor{blue}{-13x}\textcolor{#FF00FF}{+6}[/tex] | |
| [tex]\;\;\;\;-13x^2+19x-6[/tex] | ||
| [tex]\;\;\;\;\;\;\;\;\;\;\textcolor{blue}{13x^2-13x}[/tex] | ||
| [tex]\;\;\;\;6x-6\;\;\;[/tex] | ||
| [tex]\qquad \textcolor{#FF00FF}{-6x+6}\;\;[/tex] | ||
| [tex]\;\;0\;\;\;[/tex] |
Dessa forma, [tex]6x^3-19x^2+19x-6=\left(x-1\right)\cdot \left(6x^2-13x+6\right)[/tex] e, portanto, as outras raízes da equação [tex]6x^3-19x^2+19x-6=0[/tex] são as raízes de [tex]6x^2-13x+6=0[/tex].
Para essa segunda equação, basta aplicarmos a fórmula de resolução de uma equação do 2º grau:
[tex]\qquad \dfrac{13\pm\sqrt{169-144}}{12}=\dfrac{13\pm 5}{12}\\
\;[/tex]
e com isso obtemos as raízes [tex]\dfrac{2}{3}\,[/tex] e [tex]\,\dfrac{3}{2}[/tex].
Portanto, as raízes da equação [tex]6x^3-19x^2+19x-6=0[/tex] são: [tex]\fcolorbox{black}{#eee0e5}{$x_1=1$}\;[/tex]; [tex]\fcolorbox{black}{#eee0e5}{$x_2=\dfrac{3}{2}$}\,[/tex] e [tex]\,\fcolorbox{black}{#eee0e5}{$x_3=\dfrac{2}{3}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
