✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Muito Difícil)
Uma grande rede de lanchonetes oferece dois tipos de sucos que fazem o maior sucesso: o abacanja e o laranxi.
Para produzi-los, são utilizadas duas frutas, abacaxi e laranja:
- Cada litro do abacanja é produzido a partir de 0,4 litros de suco puro de abacaxi e 0,6 litros de suco puro de laranja.
- Cada litro do laranxi é produzido a partir de 0,2 litros de suco puro de abacaxi e 0,8 litros de suco puro de laranja.

Por razões comerciais, a rede de lanchonetes quer produzir semanalmente pelo menos 200 litros do abacanja e pelo menos 300 litros do laranxi. No entanto, para preservar a qualidade, as lanchonetes da rede só podem armazenar frutas suficientes para produzir no máximo 200 litros de suco puro de abacaxi e 500 litros de suco puro de laranja por semana.
Sabendo que o lucro nas vendas é de R$ 4,00 por litro do abacanja e de R$ 5,00 por litro do laranxi, qual a quantidade em litros de cada tipo de suco que essa rede de lanchonetes deve vender semanalmente para maximizar seu lucro? Qual o lucro máximo que a rede poderá obter por semana?
Solução
Sejam [tex]x[/tex] e [tex]y[/tex] as quantidades em litros dos sucos de abacanja e laranxi que a rede de lanchonetes deve vender semanalmente para maximizar seu lucro, respectivamente. Assim, a partir dos dados do problema, vamos estabelecer as restrições para [tex]x[/tex] e [tex]y[/tex]. Mas antes, vamos construir uma tabela com os dados para facilitar.
[tex]\begin{array}{|c |c| c | c| c|}
\hline
\text{Sucos}&\text{Litros a serem fabricados}&\text{Suco puro de abacaxi utilizado}&\text{Suco puro de laranja utilizado}&\text{Lucro}\\
\hline
\text{Abacanja}&x&0,4\cdot x\,\, litros & 0,6\cdot x\,\, litros & 4\cdot x\,\, reais\\
\hline
\text{Laranxi}&y&0,2\cdot y\,\, litros & 0,8\cdot y\,\, litros & 5\cdot y\,\, reais\\
\hline
\text{Totais}&x+y&(0,4\cdot x+0,2\cdot y)\,\, litros & (0,6\cdot x+0,8\cdot y)\,\, litros & (4\cdot x+5\cdot y)\,\, reais\\
\hline
\end{array}[/tex]
(1) Serão produzidos semanalmente pelo menos [tex]200[/tex] litros do abacanja. Logo:
- [tex]x \geqslant 200.[/tex]
(2) Serão produzidos semanalmente pelo menos [tex]300[/tex] litros do laranxi. Logo:
- [tex]y \geqslant 300.[/tex]
(3) Semanalmente, só podem ser armazenadas frutas suficientes para produzir no máximo [tex]200[/tex] litros de suco puro de abacaxi. Assim:
- [tex]0,4\cdot x+0,2\cdot y \leqslant 200.[/tex]
(4) Semanalmente, só podem ser armazenadas frutas suficientes para produzir no máximo [tex]500[/tex] litros de suco puro de laranja . Assim:
- [tex]0,6\cdot x+0,8\cdot y \leqslant 500.[/tex]
Por (1), (2), (3) e (4), as restrições para [tex]x[/tex] e para [tex]y[/tex] são atendidas pelos pares ordenados [tex](x,y)[/tex] tais que:
[tex]\begin{cases}
x \geqslant 200 \\
y \geqslant 300\\
0,4\cdot x+0,2\cdot y \leqslant 200\\
0,6\cdot x+0,8\cdot y \leqslant 500\\
\end{cases} \,\,\,\, .\qquad \qquad \textcolor{#800000}{(i)}[/tex]
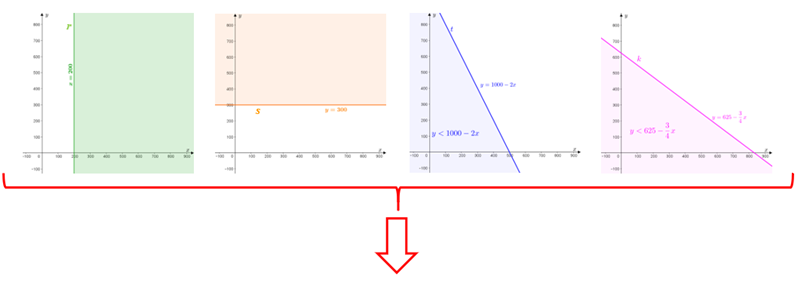
Observe que nada impede que as quantidades de litros sejam dadas por números não inteiros, já que podemos ter, por exemplo, 5 litros e meio, 10,7 litros. Então, vamos estudar cada uma dessas quatro condições isoladamente em [tex]\mathbb{R} \times \mathbb{R}[/tex] e, em seguida, analisarmos as quatro simultaneamente.
- Condição [tex]\boxed{x \geqslant 200 } [/tex]
- Condição [tex]\boxed{y \geqslant 300} [/tex]
- Condição [tex] \boxed{0,4\cdot x+0,2\cdot y \leqslant 200} [/tex]
- Condição [tex]\boxed{0,6\cdot x+0,8\cdot y \leqslant 500}[/tex]
Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:
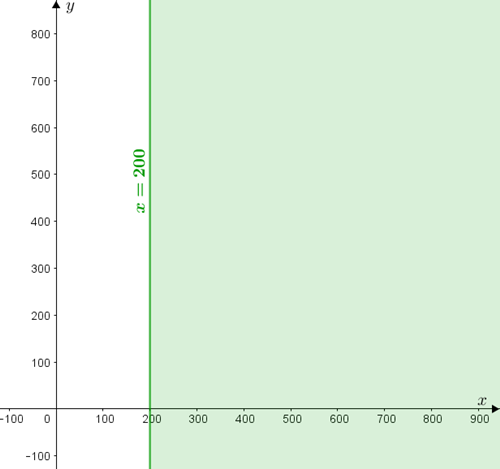
- – aqueles que estão sobre a reta [tex]r[/tex] definida por [tex]x=200 \, [/tex],
– aqueles que estão à direita da reta [tex]r[/tex] ([tex]x \gt 200 \, [/tex]).
A reta [tex]r[/tex] é a reta vertical que intersecta o eixo [tex]Ox[/tex] em [tex]x=200 .[/tex]
Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:
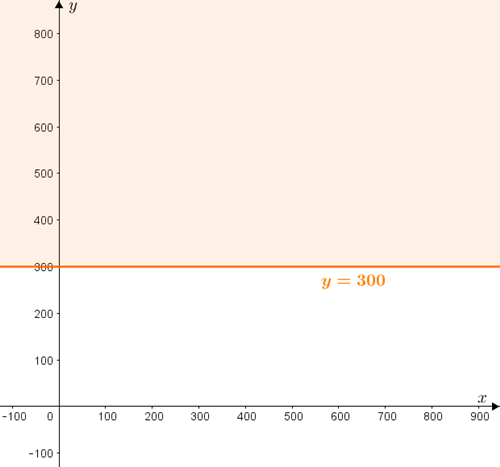
- – aqueles que estão sobre a reta [tex]s[/tex] definida por [tex]y=300 \, [/tex],
– aqueles que estão acima da reta [tex]s[/tex] ([tex]y \gt 300 \, [/tex]).
A reta [tex]s[/tex] é a reta horizontal que intersecta o eixo [tex]Oy[/tex] em [tex]y=300 .[/tex]
Observe que
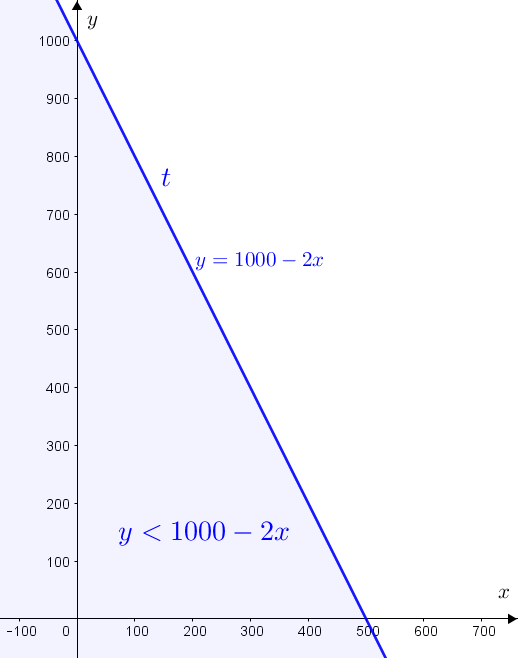
[tex]\qquad 0,4x+0,2y \leqslant 200 \iff 2x+y \leqslant 1000 \iff y \leqslant 1000-2x [/tex],
assim, os pontos [tex]P=(x,y)[/tex] que satisfazem esta terceira condição são:
- – aqueles que estão sobre a reta [tex]t[/tex] definida por [tex]y=1000-2x \, [/tex] (e satisfazem a igualdade [tex]0,4\cdot x+0,2\cdot y =200[/tex]);
– aqueles que estão abaixo da reta [tex]t[/tex] (e satisfazem a desigualdade [tex]0,4\cdot x+0,2\cdot y \lt 200[/tex]).
A reta [tex]t[/tex] é a reta que intersecta os eixos [tex]Ox[/tex] e [tex]Oy[/tex] em [tex]x=500 [/tex] e [tex]y=1000[/tex], respectivamente.
Observe que:
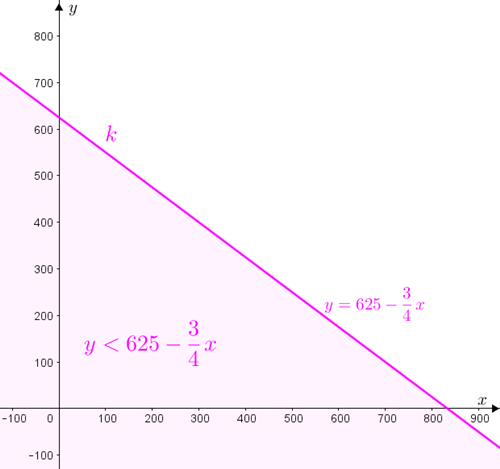
[tex]\qquad 0,6x+0,8y \leqslant 500 \iff \dfrac{3}{4}x+ y \leqslant 625\iff y \leqslant 625-\dfrac{3}{4}x[/tex],
assim, os pontos [tex]P=(x,y)[/tex] que satisfazem esta última condição são:
- – aqueles que estão sobre a reta [tex]k[/tex] definida por [tex]y=625-\dfrac{3}{4} \, x[/tex] (e satisfazem a igualdade [tex]0,6 x+0,8 y = 500[/tex]),
– aqueles que estão abaixo da reta [tex]k[/tex] (e satisfazem a desigualdade [tex]0,6\cdot x+0,8\cdot y \lt 500[/tex]).
A reta [tex]k[/tex] é a reta que intersecta os eixos [tex]Ox[/tex] e [tex]Oy[/tex] em [tex]x=\frac{2500}{3}\approx 833 [/tex] e [tex]y=625[/tex], respectivamente.
Fazendo a interseção das quatro regiões acima, obtemos a solução do sistema [tex]\textcolor{#800000}{(i)}[/tex] em [tex]\mathbb{R} \times \mathbb{R}.[/tex]
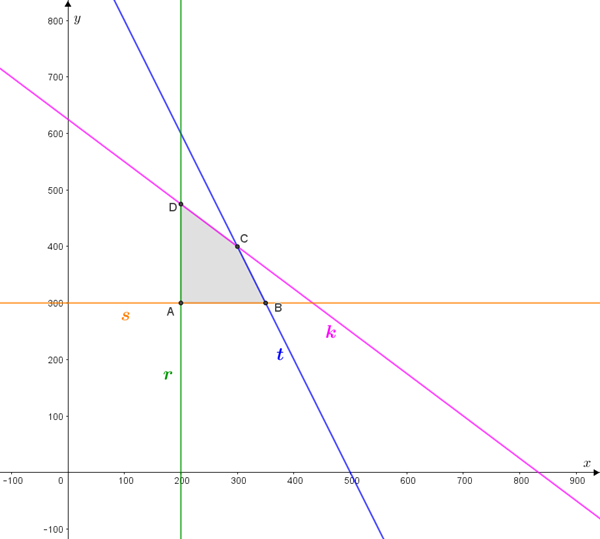
Portanto, os pares ordenados que satisfazem as condições (1), (2), (3) e (4), são aqueles que definem os pontos do quadrilátero [tex]ABCD[/tex] e de seu interior. Para melhor precisar essa região, vamos determinar as coordenadas dos vértices do quadrilátero [tex]ABCD.[/tex]
- O ponto [tex]A[/tex] é a interseção das retas [tex]r[/tex] e [tex]s[/tex]; assim, [tex]A=(200,300).[/tex]
- O ponto [tex]B[/tex] é a interseção das retas [tex]t[/tex] e [tex]s[/tex]; assim, [tex]y_B=300[/tex] e, portanto,
- O ponto [tex]C[/tex] é a interseção das retas [tex]t[/tex] e [tex]k[/tex]; assim:
- O ponto [tex]D[/tex] é a interseção das retas [tex]r[/tex] e [tex]k[/tex]; assim, [tex]x_D=200[/tex] e, portanto,
[tex]\qquad y_B=1000-2x_B[/tex]
[tex]\qquad 300=1000-2x_B[/tex]
[tex]\qquad 2x_B=700[/tex]
[tex]\qquad x_B=350.[/tex]
Logo, [tex]B=(350,300).[/tex]
[tex]\qquad \begin{cases}
y_C=1000-2x_C\\
y_C=625-\frac{3}{4}x_C\end{cases}[/tex]
[tex]\qquad 1000-2x_c=625-\frac{3}{4}x_C[/tex]
[tex]\qquad 4000-8x_c=2500-3x_C[/tex]
[tex]\qquad 5x_C=1500[/tex]
[tex]\qquad x_C=300[/tex]
[tex]\qquad y_C=1000-2\times 300[/tex]
[tex]\qquad y_C=400.[/tex]
Logo, [tex]C=(300,400).[/tex]
[tex]\qquad y_D=625-\frac{3}{4}x_D[/tex]
[tex]\qquad y_D=625-\frac{3}{4}\times 200[/tex]
[tex]\qquad y_D=625-150[/tex]
[tex]\qquad y_D=475.[/tex]
Logo, [tex]D=(200,475).[/tex]
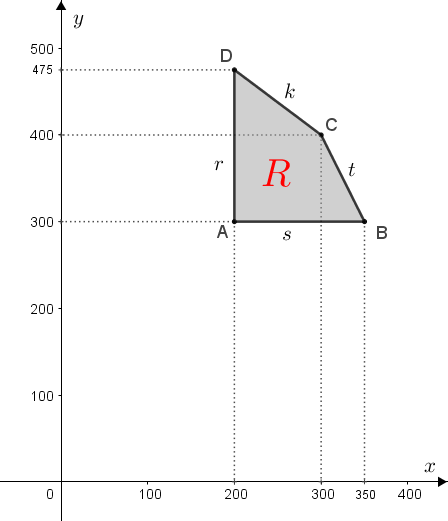
O lucro que a rede de lanchonetes obtém nas vendas é de R$ 4,00 por litro do abacanja e de R$ 5,00 por litro do laranxi, portanto o lucro [tex]L[/tex] obtido semanalmente com a venda de [tex]x[/tex] litros do abacanja e de [tex]y[/tex] litros do laranxi é dado pela equação [tex]\boxed{L=4\cdot x+5\cdot y}.[/tex]
Temos, então uma função [tex]L[/tex] de duas variáveis, definida por [tex]L(x,y)=4\cdot x+5\cdot y[/tex], para a qual precisamos saber o valor máximo que ela assume dentre os pares ordenados [tex](x,y)[/tex] da região [tex]\textcolor{red}{R}[/tex] definida pelo quadrilátero [tex]ABCD.[/tex] São infinitos pares ordenados; logo, não podemos calcular [tex]L(x,y)[/tex] para cada um deles. Mas note que, para cada número real [tex]m[/tex], a equação [tex]4\cdot x+5\cdot y=m[/tex] descreve uma reta.
Assim, podemos analisar geometricamente a família de retas paralelas descritas por [tex]4x+5y=z[/tex], para números reais positivos [tex]z[/tex], no plano cartesiano no qual esteja representada a região [tex]\textcolor{red}{R}.[/tex]
A interseção de cada uma dessas retas com a região [tex]\textcolor{red}{R}[/tex] determina os pontos cujas coordenadas definem as quantidades em litros dos dois sucos cujas vendas propiciam o lucro [tex]z[/tex] que define a reta em questão.
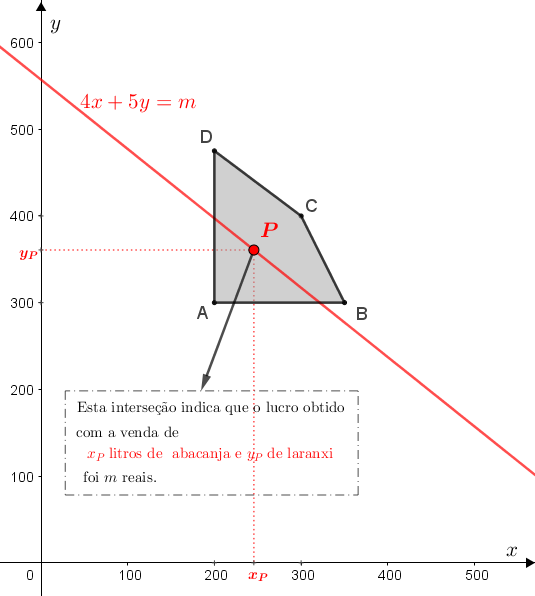
Para facilitar a análise, podemos utilizar o applet abaixo.
No aplicativo podemos visualizar um plano cartesiano [tex]xOy[/tex] e a região [tex]\textcolor{red}{R}[/tex]. Vemos também a reta definida pela equação [tex]4\cdot x+5\cdot y=1[/tex]; esta é a primeira reta da família de retas [tex]4\cdot x+5\cdot y=z[/tex], na qual a variável [tex]z[/tex] representa o lucro obtido semanalmente com a venda de [tex]x[/tex] litros do abacanja e de [tex]y[/tex] litros do laranxi. As demais retas dessa família são obtidas movimentando-se horizontalmente o ponto que aparece na parte inferior esquerda do applet, sobre o segmento verde. Esse ponto indicará valores de [tex]1[/tex] a [tex]3500[/tex], valores estes que representarão lucros de [tex]R\$ \, 1,00[/tex] a [tex]R\$ \, 3\,500,00[/tex] com a venda dos dois sucos.
Para cada reta obtida com a movimentação do ponto Lucro, a sua equação será exibida na parte superior do applet, a direita.
Com o applet observamos que, para os pontos que nos interessam, o lucro é maior do que [tex]R\$ \, 2\,000,00[/tex], assim, vamos apresentar outro applet no qual a primeira reta da família de retas [tex]4\cdot x+5\cdot y=z[/tex] é a que tem como equação [tex]4\cdot x+5\cdot y=2000.[/tex]
Com esse último applet, fica mais evidente que o ponto que fornece o valor máximo da função [tex]L(x,y)[/tex] é o vértice [tex]C[/tex] da região [tex]\textcolor{red}{R}.[/tex] Para melhorar o entendimento sobre os valores do Lucro, vamos calcular o valor da função [tex]L(x,y)[/tex] em cada um dos vértices da região:
- [tex]A=(200,300)[/tex]
- [tex]B=(350,300)[/tex]
- [tex]C=(300,400)[/tex]
- [tex]D=(200,475)[/tex]
Observe que [tex]L(200,300)=4\times 200+5\times 300=2\,300[/tex]; assim, o lucro semanal obtido pela rede de lanchonetes com a venda de [tex]200[/tex] litros de abacanja e [tex]300[/tex] litros de laranxi será [tex]R\$ \, 2\,300,00.[/tex]
Observe que [tex]L(350,300)=4\times 350+5\times 300=2\,900[/tex]; assim, o lucro semanal obtido pela rede de lanchonetes com a venda de [tex]200[/tex] litros de abacanja e [tex]300[/tex] litros de laranxi será [tex]R\$ \, 2\,900,00.[/tex]
Observe que [tex]L(300,400)=4\times 300+5\times 400=3\,200[/tex]; assim, o lucro semanal obtido pela rede de lanchonetes com a venda de [tex]200[/tex] litros de abacanja e [tex]300[/tex] litros de laranxi será [tex]R\$ \, 3\,200,00.[/tex]
Observe que [tex]L(200,475)=4\times 200+5\times 475=3\,175[/tex]; assim, o lucro semanal obtido pela rede de lanchonetes com a venda de [tex]200[/tex] litros de abacanja e [tex]300[/tex] litros de laranxi será [tex]R\$ \, 3\,175,00.[/tex]
Portanto, a rede de lanchonetes deve vender semanalmente [tex]300[/tex] litros de abacanja e [tex]400[/tex] litros de laranxi para maximizar seu lucro com a venda desses dois sucos. Nesse caso, o lucro máximo que a rede poderá obter por semana será [tex] \fcolorbox{black}{#eee0e5}{$R\$ \, 3\,200,00$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
