✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
(OPM – 2004) Para construir a pipa de papel mostrada na figura à esquerda, Joãozinho traçou um retângulo [tex]ABCD[/tex] numa folha de papel e pintou o seu interior.
Em seguida, Joãozinho prolongou cada um dos lados do retângulo pintado, triplicando o comprimento de cada um. Com isso ele obteve o quadrilátero [tex]EFGH[/tex], conforme mostrado na figura ampliada, à direita.
Por fim, Joãozinho pintou os quatro triângulos resultantes da construção, colocou uma rabiola colorida e partiu para brincar…
 |
 |
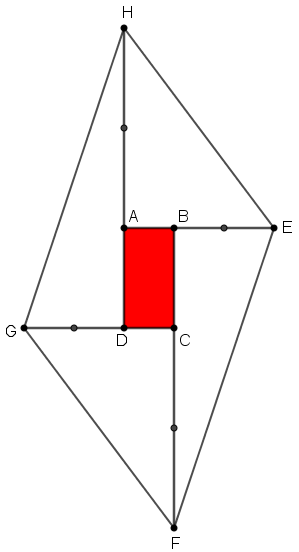Sabendo que a área do retângulo inicial pintado por Joãozinho é [tex]4\, cm^2[/tex], determine a área da pipa que ele construiu.
(Para efeito dos cálculos, não considere a rabiola)
Solução
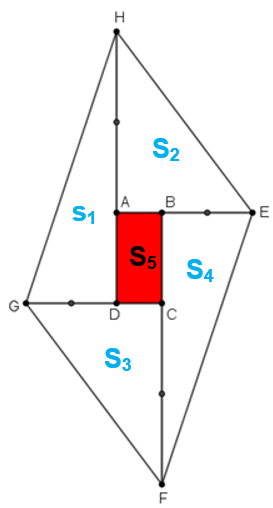Observe que a área da pipa, sem a rabiola, é a soma da área dos triângulos [tex]HDG[/tex] ; [tex]FBE[/tex] ; [tex]HAE[/tex] e [tex]FCG[/tex] e do retângulo [tex]ABCD\, .[/tex] Como os quatro triângulos foram construídos prolongando-se os lados do retângulo [tex]ABCD\, [/tex], eles são triângulos retângulos e, portanto, suas áreas podem ser calculadas utilizando-se os respectivos catetos como bases e alturas.
Vamos aos cálculos:
- [tex]S_1=\dfrac{GD \times HD}{2}=\dfrac{\cancel{2}DC \times 3AD}{\cancel{2}}=AB \times 3AD[/tex]
- [tex]S_2=\dfrac{HA \times AE}{2}=\dfrac{\cancel{2}AD\times 3AB}{\cancel{2}}=AD \times 3AB[/tex]
- [tex]S_3=\dfrac{FC \times CG}{2}=\dfrac{\cancel{2}BC\times 3DC}{\cancel{2}}=AD \times 3AB[/tex]
- [tex]S_4=\dfrac{FB \times BE}{2}=\dfrac{3BC\times \cancel{2}AB}{\cancel{2}}=AB \times 3AD[/tex]
- [tex]S_5=AB \times AD\, .[/tex]
Assim, a área [tex]S[/tex] da pipa é:
[tex]\qquad S=S_1+S_2+S_3+S_4+S_5[/tex]
[tex]\qquad S=AB \times 3AD+AD \times 3AB+AD \times 3AB+AB \times 3AD+AB \times AD[/tex]
[tex]\qquad S=3 \times AB \times AD+3 \times AB \times AD+3 \times AB \times AD+3 \times AB \times AD+AB \times AD[/tex]
[tex]\qquad S=\left(3+3+3+3+1 \right) \times AB \times AD[/tex]
[tex]\qquad S=13 \times \left(AB \times AD \right)\, .[/tex]
Pelos dados do problema, [tex]S_5=AB \times AD=4\, cm^2\, [/tex], logo:
[tex]\qquad S=13 \times \left(AB \times AD \right)=13 \times 4=52\, cm^2\, .[/tex]
Assim, a área da pipa que Joãozinho construiu é [tex]\, \fcolorbox{black}{#eee0e5}{$52\, cm^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |