✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio )
Seja [tex]f[/tex] a função definida por
[tex]\qquad \qquad f(x)=\begin{cases} x+2 \, \, \, \text{, se } 0 \leqslant x \leqslant 2\\
\\
6-x \text{, se } 2\lt x \leqslant 6
\end{cases}[/tex]
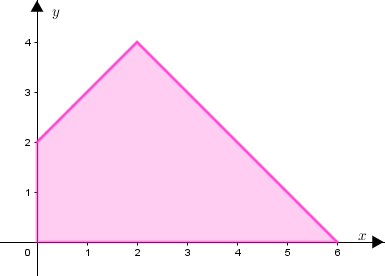
Determinar a área da região limitada pelo gráfico da função [tex]f[/tex] e pelas retas definidas por [tex]x=0\, [/tex] e [tex]\, y=0.[/tex]
Solução
Vamos traçar inicialmente as retas definidas por [tex]\textcolor{y=x+2}{y=x+2}\, [/tex] e [tex]\, \textcolor{y=x+2}{y=6-x}[/tex] para obtermos o gráfico da função [tex]f\, .[/tex]
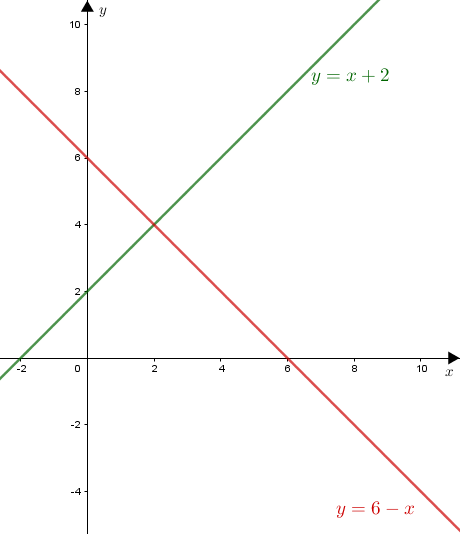
Observe que as retas se cortam quando [tex]y=x+2=6-x[/tex], ou seja, no ponto [tex](2,4)\, .[/tex]
Este é o gráfico da função [tex]f\, [/tex]
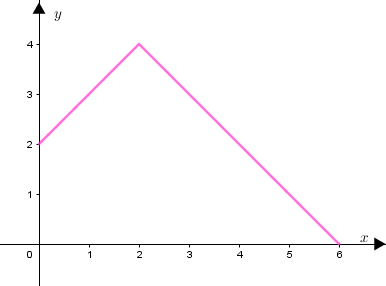
e esta é a região cuja área vamos calcular.
Observe que podemos decompor a região em questão em um trapézio e em um triângulo retângulo, conforme vemos na figura a seguir.
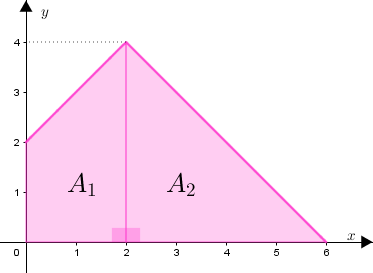
Com isso, a área a ser determinada é a soma das áreas [tex]A_1\, [/tex] e [tex]\, A_2\, .[/tex]
Observe que:
[tex]\qquad A_1=\dfrac{\left(\text{base maior+base menor}\right)\times \text{altura}}{2}[/tex]
[tex]\qquad A_1=\dfrac{\left(4+2\right)\times 2}{2}[/tex]
[tex]\qquad \boxed{A_1=6\, \text{unidades de área}}[/tex]
e
[tex]\qquad A_2=\dfrac{\text{base}\times \text{altura}}{2}[/tex]
[tex]\qquad A_2=\dfrac{4 \times 4}{2}[/tex]
[tex]\qquad \boxed{A_2=8\, \text{unidades de área}}\, .[/tex]
Assim, a área da região limitada pelo gráfico da função [tex]f[/tex] e pelas retas definidas por [tex]x=0\, [/tex] e [tex]\, y=0[/tex] é:
[tex]\, \fcolorbox{black}{#eee0e5}{$ A_1+A_2=\text{14 unidades de área}$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
