✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M.)
Na figura, o hexágono regular [tex]ABCDEF [/tex] está inscrito no círculo de centro [tex]O. [/tex]
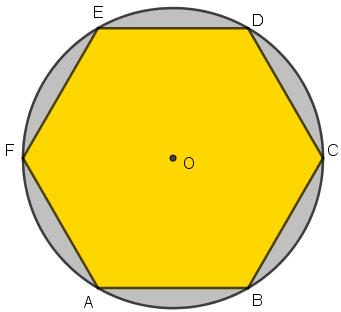
Se a distância entre os vértices [tex]A\, [/tex]e [tex]\, B[/tex] é [tex]4\, [/tex]cm, qual a área do quadrilátero [tex]ABOF\, ?[/tex]

Lembretes para a Solução 1
(1) Caso de congruência L.L.L. (lado – lado – lado): Se dois triângulos têm ordenadamente congruentes os três lados, então estes triângulos são congruentes. (Se você não se lembra dos casos de congruência de triângulos, clique AQUI.)
(2) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
(3) Todo triângulo isósceles possui os ângulos da base com a mesma medida.
(4) A bissetriz de um triângulo equilátero também é uma mediana e uma altura.
(5) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução 1
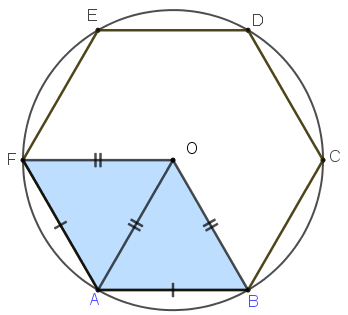
Na figura ao lado, destacamos o quadrilátero [tex]ABOF[/tex] cuja área iremos calcular.
Observe inicialmente que a área desse quadrilátero é a soma das áreas dos triângulos [tex]AOB[/tex] e [tex]FOA[/tex]; assim, vamos obter as áreas desses triângulos.
Uma primeira análise nos mostra que:
- os segmentos [tex]\overline{OB}[/tex], [tex]\overline{OA}[/tex] e [tex]\overline{OF}[/tex] são congruentes, pois são raios do círculo no qual o hexágono [tex]ABCDEF [/tex] está inscrito;
- os segmentos [tex]\overline{BA}[/tex] e [tex]\overline{AF}[/tex] também são congruentes, pois são lados do hexágono regular [tex]ABCDEF.[/tex]
Logo, pelo Lembrete (1), os triângulos [tex]AOB[/tex] e [tex]FOA[/tex] são congruentes e, com isso, precisamos encontrar a área de apenas um deles. Por oferecer uma melhor visualização, calcularemos a área do triângulo [tex]AOB.[/tex]
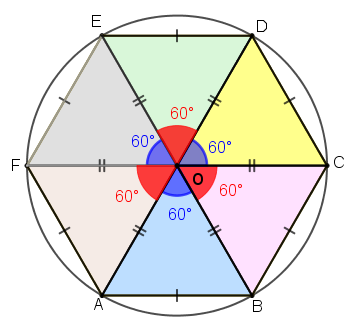
Observe que:
- dois dos lados de cada um deles são raios do círculo no qual o hexágono [tex]ABCDEF [/tex] está inscrito; logo, esses doze segmentos são congruentes;
- os terceiros lados de cada um desses triângulos são lados do hexágono [tex]ABCDEF [/tex], que é regular. Portanto, esses seis segmentos também são congruentes entre si.
Utilizando seguidamente o Lembrete (1), concluímos que os seis triângulos destacados na figura são congruentes e esse fato nos permite concluir que os ângulos internos desses seis triângulos com vértices no ponto [tex]O[/tex] têm a mesma medida, que em graus é igual a [tex]\dfrac{360^\circ}{6}=60^\circ[/tex]. Então, particularmente a medida do ângulo [tex]A\hat{O}B[/tex] é [tex]60^\circ .[/tex]
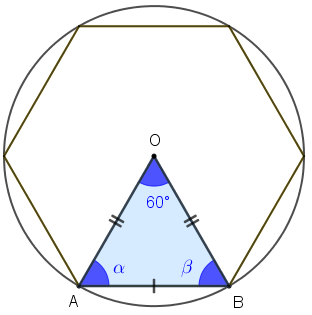
Sabemos que o ângulo interno com vértice em [tex]O[/tex] desse triângulo mede [tex]60^\circ[/tex]; vamos calcular a medida dos outros dois ângulos internos. Para tal, denotaremos essas medidas por [tex]\alpha[/tex] e [tex]\beta[/tex], conforme indicado na figura à direita.
Pelo Lembrete (2), segue que:
[tex]\qquad \alpha+\beta+60^\circ=180^\circ\\
\qquad \alpha+\beta=180^\circ -60^\circ\\
\qquad \alpha+\beta=120^\circ \qquad \qquad \textcolor{#800000}{(i)}[/tex]
e pelo Lembrete (3) temos que:
[tex]\qquad \alpha = \beta. \qquad \qquad \textcolor{#800000}{(ii)}[/tex]
Então, por [tex] \textcolor{#800000}{(i)}\, [/tex] e [tex]\, \textcolor{#800000}{(ii)}[/tex], vem que:
[tex] \qquad \alpha+\beta=120^\circ [/tex]
[tex] \qquad \alpha+\alpha=120^\circ [/tex]
[tex] \qquad 2\, \alpha=120^\circ [/tex]
[tex] \qquad\alpha=\beta=60^\circ [/tex]
e com isso concluímos que o triângulo [tex]AOB[/tex] é equilátero. Dessa forma, como a distância entre os vértices [tex]A\, [/tex] e [tex]\, B[/tex] é [tex]4\, [/tex]cm, os três lados do triângulo [tex]AOB[/tex] têm comprimento [tex]4\, [/tex]cm.
Ainda não temos condições de calcular a área do triângulo [tex]AOB[/tex]. Como a área de um triângulo é [tex]\dfrac{\text{base} \times \text{altura}}{2}[/tex], precisamos calcular a altura desse triângulo. Para isso, seja [tex]h[/tex] a medida da altura em centímetros do triângulo [tex]AOB.[/tex]
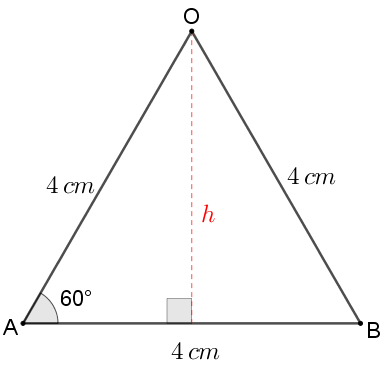
Utilizando o Lembrete (4) e o Teorema de Pitágoras, segue que:
[tex]\qquad h^2+\left(\dfrac{4}{2}\right)^2=4^2[/tex]
[tex]\qquad h^2+4=16[/tex]
[tex]\qquad h^2=12[/tex]
[tex]\qquad h=\pm\sqrt{3\times 4}[/tex]
[tex]\qquad h=2\sqrt{3}[/tex], já que [tex]h \gt 0.[/tex]
Logo, a área [tex]S[/tex] do triângulo [tex]AOB[/tex] já pode ser calculada:
[tex]\qquad S=\dfrac{\text{base} \times \text{altura}}{2}=\dfrac{4 \times 2\sqrt{3}}{2}=4\sqrt{3}\text{ cm}^2[/tex]
e consequentemente temos a área do quadrilátero [tex]ABOF:[/tex] [tex]\, \fcolorbox{black}{#eee0e5}{$ 2 \times 4\sqrt{3}=8\sqrt{3}\approx13,86\text{ cm}^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembretes para a Solução 2
(1) Todo hexágono regular pode ser decomposto em seis triângulos equiláteros congruentes.
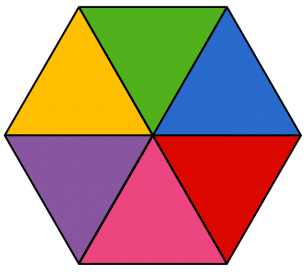
(2) A área [tex]A[/tex] de um triângulo equilátero de lado com comprimento [tex]l[/tex] é [tex]A=\dfrac{l^2\sqrt{3}}{4}[/tex].
Solução 2
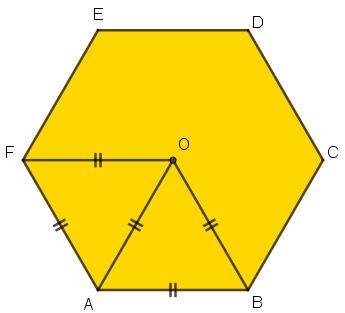
Na figura ao lado, destacamos o quadrilátero [tex]ABOF[/tex] cuja área iremos calcular.
Pelo Lembrete (1), o hexágono regular [tex]ABCDEF [/tex] pode ser decomposto em seis triângulos equiláteros congruentes; assim, a área do quadrilátero [tex]ABOF[/tex] é a soma das áreas dos triângulos equiláteros congruentes [tex]AOB[/tex] e [tex]FOA[/tex]. Com isso, se [tex]A_{q}[/tex] e [tex]A_{t}[/tex] são, respectivamente, as áreas do quadrilátero [tex]ABOF[/tex] e de cada triângulo equilátero que compõe o hexágono [tex]ABCDEF[/tex], então:
[tex]\qquad A_{q}= 2 A_{t}. \qquad \qquad \textcolor{#800000}{(i)} [/tex]
Por outro lado, pelo Lembrete (2), segue que:
[tex]\qquad A_{t}=\dfrac{4^2\sqrt{3}}{4}[/tex]
[tex]\qquad A_{t}=4\sqrt{3}. \qquad \qquad \textcolor{#800000}{(ii)}[/tex]
Assim, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\qquad A_{q}= 2 \times 4\sqrt{3} [/tex]
[tex]\qquad A_{q}= 8\sqrt{3}. [/tex]
Portanto, a área do quadrilátero [tex]ABOF[/tex] é [tex]\, \fcolorbox{black}{#eee0e5}{$8\sqrt{3}\approx13,86\text{ cm}^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
