Problema
Com base na figura abaixo, determinar, em graus, [tex]x+y[/tex].
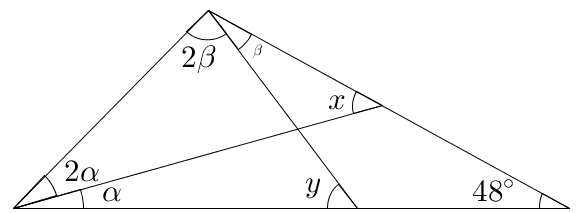
Solução
Para um melhor entendimento, vamos nomear alguns pontos da figura:
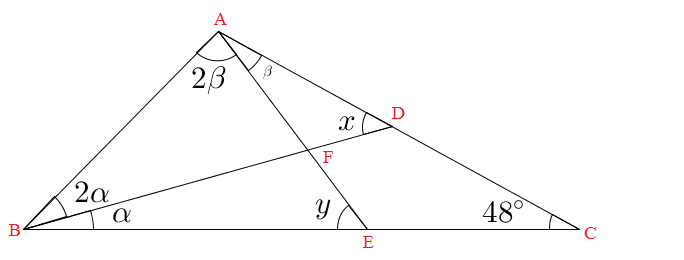
Considerando que a soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]*, temos então:
[tex]\quad \triangle ABC[/tex]:
[tex]\qquad \alpha+2\alpha+2\beta+\beta+48=180[/tex]
[tex]\qquad 3\alpha+3\beta=180-48[/tex]
[tex]\qquad 3\alpha+3\beta=132[/tex]
[tex]\qquad \alpha+\beta=44[/tex];
[tex]\quad \triangle ABD[/tex]:
[tex]\qquad \beta+2\beta+2\alpha+x=180\\\qquad 3\beta+2\alpha+x=180;[/tex]
[tex]\quad \triangle ABE[/tex]:
[tex]\qquad 2\beta+2\alpha+\alpha+y=180\\\qquad 2\beta+3\alpha+y=180.[/tex]
Somando as equações obtidas dos triângulos [tex]ABD[/tex] e [tex]ABE[/tex], temos:
[tex]\qquad \left(3\beta+2\alpha +x\right)+\left(2\beta+3\alpha+y\right)=180+180[/tex]
[tex]\qquad 5\beta+5\alpha+x+y=360[/tex]
[tex]\qquad x+y=360-5\beta-5\alpha[/tex].
De [tex] \, x+y=360-5\beta-5\alpha[/tex], segue que [tex] \, x+y=360-5( \alpha+\beta)[/tex].
Mas sabemos que [tex] \, \alpha+\beta=44[/tex], logo
[tex] \qquad x+y=360-5 \times44=360- 220=140[/tex].
Assim, [tex]\fbox{$ \, x+y=140^{\circ}$} \, [/tex].
(*) Visite a nossa Sala de Estudos Soma dos ângulos internos de um triângulo.
Solução elaborada pela aluna do PIC-OBMEP Bruna Fernanda Fistarol, com contribuições dos Moderadores do Blog.
