Problema
Um retângulo corta uma circunferência como é mostrado na figura abaixo.
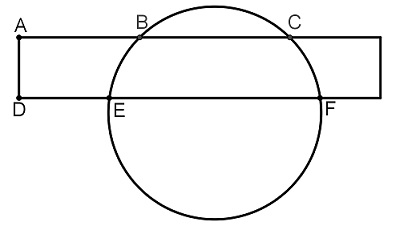
Se os segmentos AB, BC e DE medem, respectivamente, 4 , 5 e 3 unidades de comprimento, quanto mede o segmento EF?
a) [tex]6[/tex]
b) [tex]7[/tex]
c) [tex]\dfrac{20}{3}[/tex]
d) [tex]8[/tex]
e) [tex]9[/tex]
Solução
Trace o segmento BP, passando por P e perpendicular ao segmento AC. Consequentemente, BP será também perpendicular ao segmento DF e ficaremos com a figura a seguir.
Devido ao paralelismo dos segmentos AB e DP, assim como dos segmentos AD e BP, podemos concluir que a medida do segmento EP é 1 unidade de comprimento.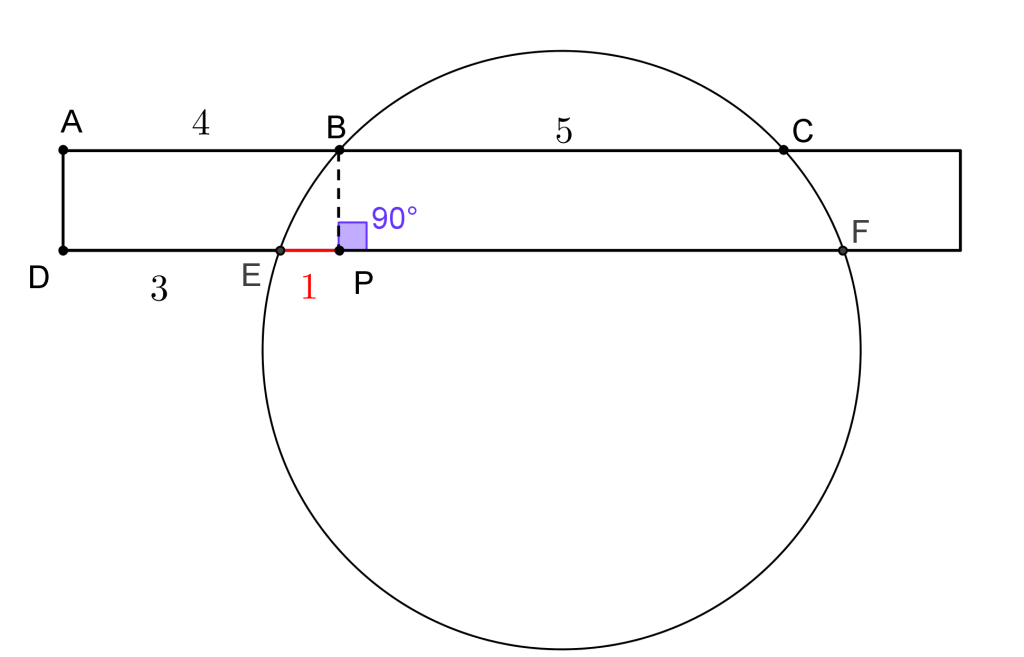
Trace, agora, o segmento CQ, passando por C e, também, perpendicular ao segmento AC. Temos, então, mais um segmento perpendicular a DF.
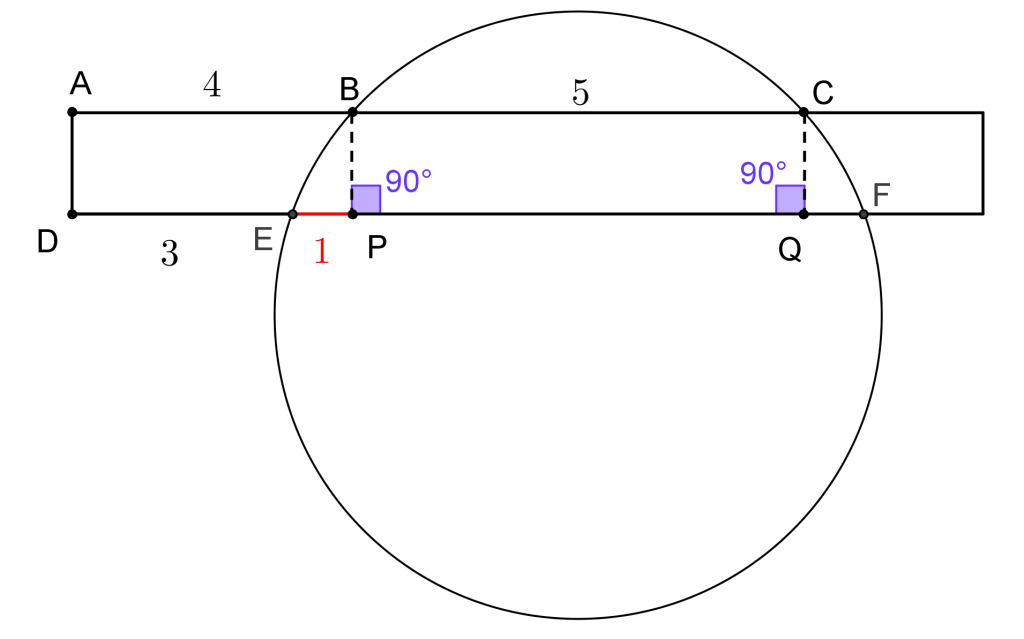Devido ao paralelismo dos segmentos BC e PQ, assim como dos segmentos BP e CQ, concluímos que a medida do segmento PQ é 5 unidades de comprimento.
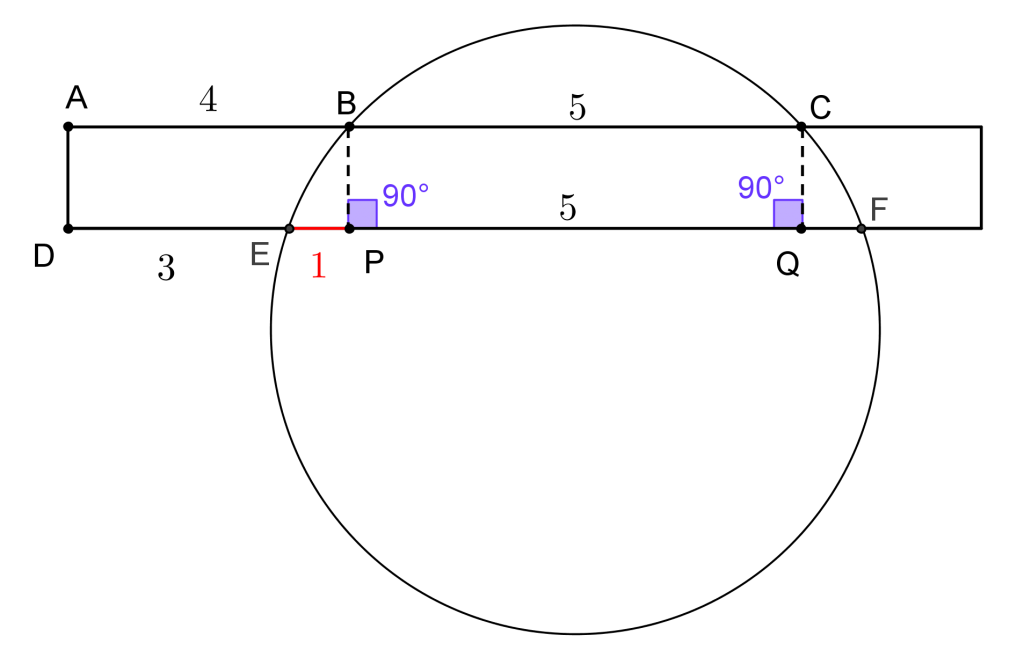É “bastante intuitivo” perceber, então, que o comprimento do segmento QF será também 1 e, dessa forma, o segmento EF terá 7 unidades de medida de comprimento.
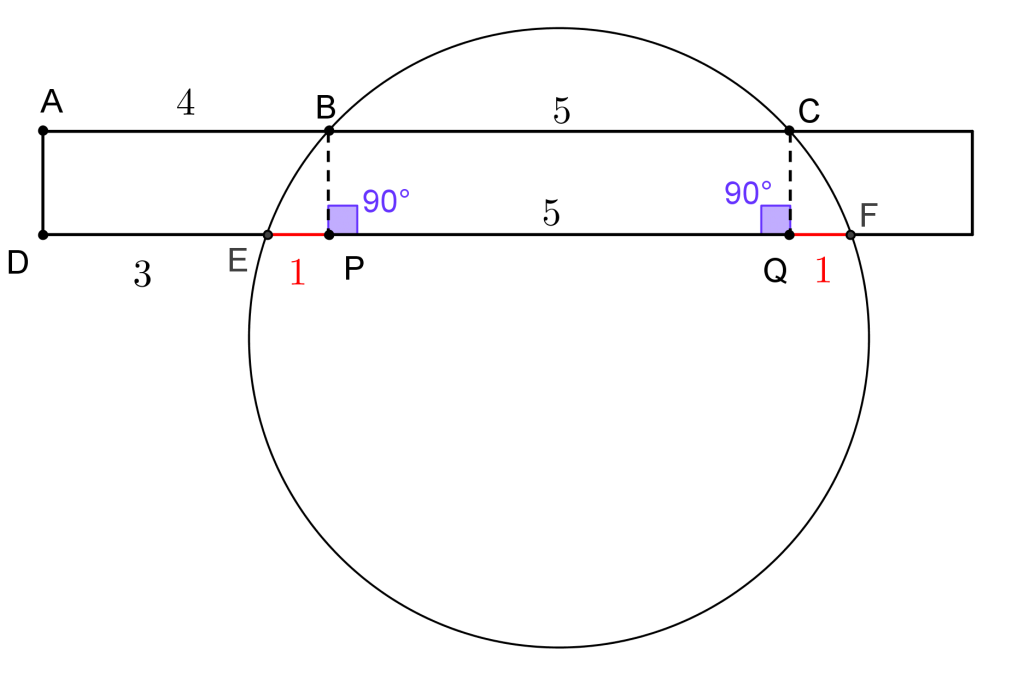Para efeito da Gincana, a resposta [tex] \,\fcolorbox{black}{#eee0e5}{$7$}\,[/tex] seria suficiente; mas vocês saberiam justificar o tal “passo intuitivo”?
Dica: O trapézio BCFE tem os quatro vértices em uma circunferência; assim é um trapézio cíclico, ou inscritível. Utilize a propriedade que garante que, sendo cíclico, esse trapézio é isósceles, ou seja, os segmentos BE e CF têm o mesmo comprimento.
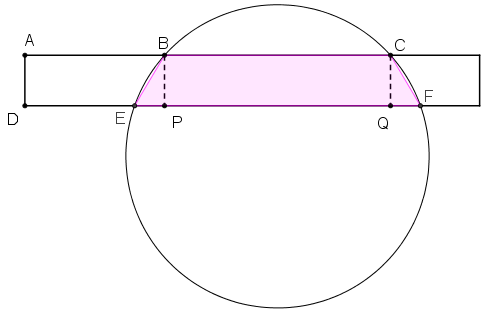
33568Solução elaborada pelos Moderadores do Blog.
Nível C – Questão Média