Problema
(Indicado a partir do 9º ano do E. F.)
Abaixo temos um quadrado [tex]ABCD[/tex] de lado [tex]4\text{ cm}[/tex] e centro [tex]X[/tex]. Sabe-se que [tex]AE = BF = 1\text{ cm}[/tex].
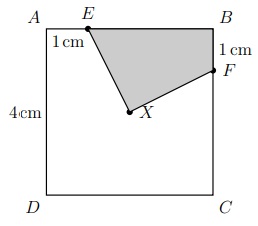
Qual a área do quadrilátero [tex]XEBF[/tex]?
Extraído de OMERJ.

Lembretes e notações
✐ Caso de congruência L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes. (Se você não se lembra dos casos de congruência de triângulos, clique AQUI.)
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline {XY} [/tex], e o seu comprimento por [tex]XY.[/tex]
Solução 1
Sejam [tex]P[/tex] e [tex]Q[/tex] os pontos médios dos lados [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex], respectivamente. Vamos construir os segmentos [tex]\overline{XP}[/tex] e [tex]\overline{XQ}[/tex]. Como [tex]X[/tex] é o centro do quadrado, os segmentos [tex]\overline{XP}[/tex] e [tex]\overline{XQ}[/tex] são perpendiculares aos segmentos [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex], respectivamente (você conseguiria provar essa afirmação?). Além disso, [tex]\overline{AP}[/tex], [tex]\overline{PB}[/tex], [tex]\overline{BQ}[/tex] e [tex]\overline{QC}[/tex] têm a mesma medida (metade do lado do quadrado). Como [tex]AE=BF[/tex], podemos concluir que [tex]EP=FQ[/tex].
Logo, os triângulos [tex]XPE[/tex] e [tex]XQF[/tex] são triângulos retângulos congruentes pelo caso [tex]L.A.L.[/tex], como ilustrado na figura abaixo:
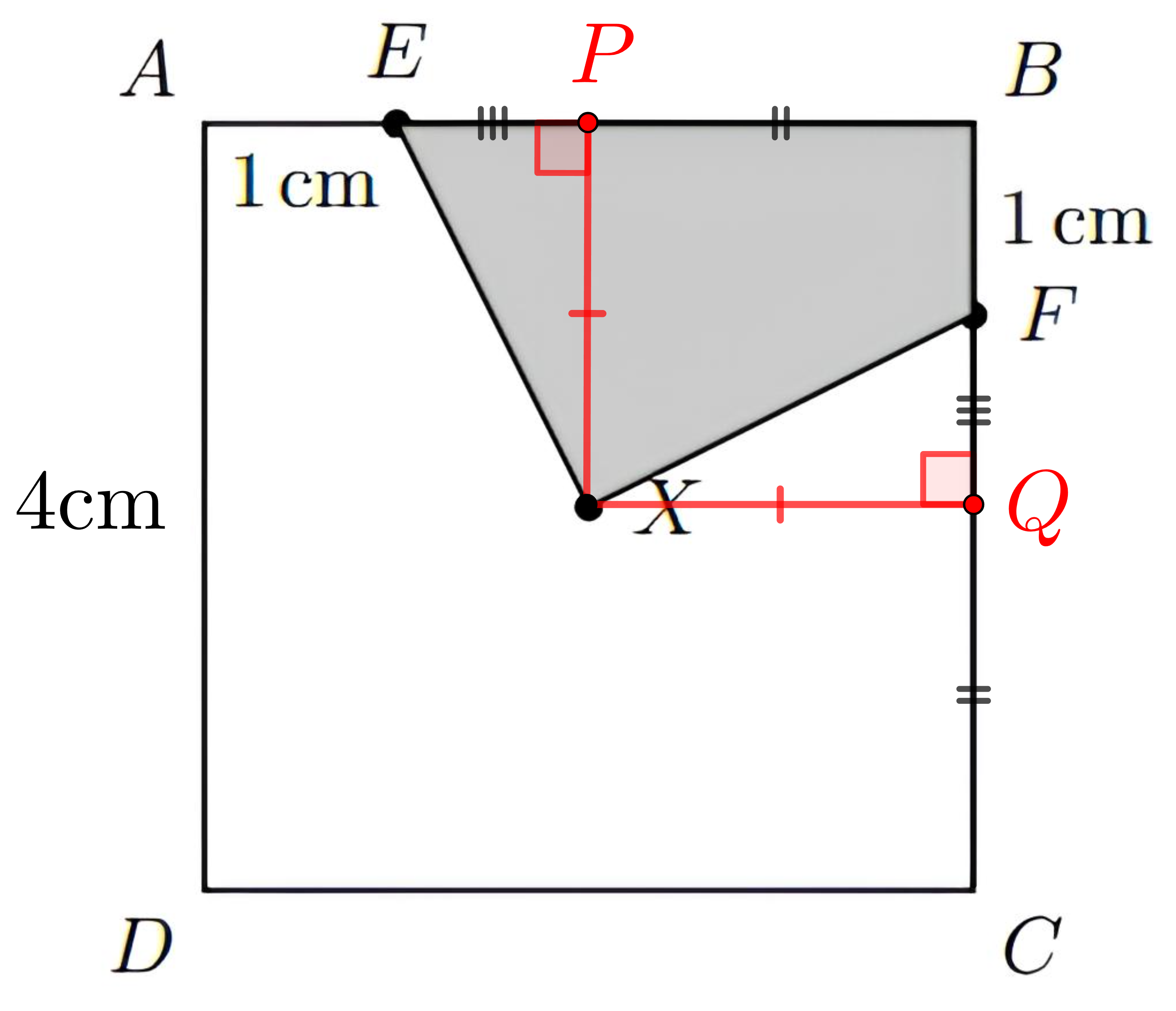
Assim, já que as áreas desses triângulos são iguais, a área do quadrilátero [tex]XEBF[/tex] é igual à área do quadrado [tex]XPBQ[/tex], que equivale a um quarto da área do quadrado [tex]ABCD[/tex].
Portanto, a área pedida é de [tex]\dfrac{16}{4}=\boxed{4\text{ cm}^2}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Seja [tex]P[/tex] o ponto médio do lado [tex]\overline{AB}[/tex]. Como [tex]X[/tex] é o centro do quadrado, o segmento [tex]\overline{XP}[/tex] é perpendicular ao segmento [tex]\overline{AB}[/tex]. Sabendo que o lado do quadrado mede [tex]4\text{ cm}[/tex], podemos calcular a área pedida como a soma das áreas de um triângulo retângulo de catetos [tex]1\text{ cm}[/tex] e [tex]2\text{ cm}[/tex] e um trapézio de bases [tex]1\text{ cm}[/tex] e [tex]2\text{ cm}[/tex] e altura [tex]2\text{ cm}[/tex].
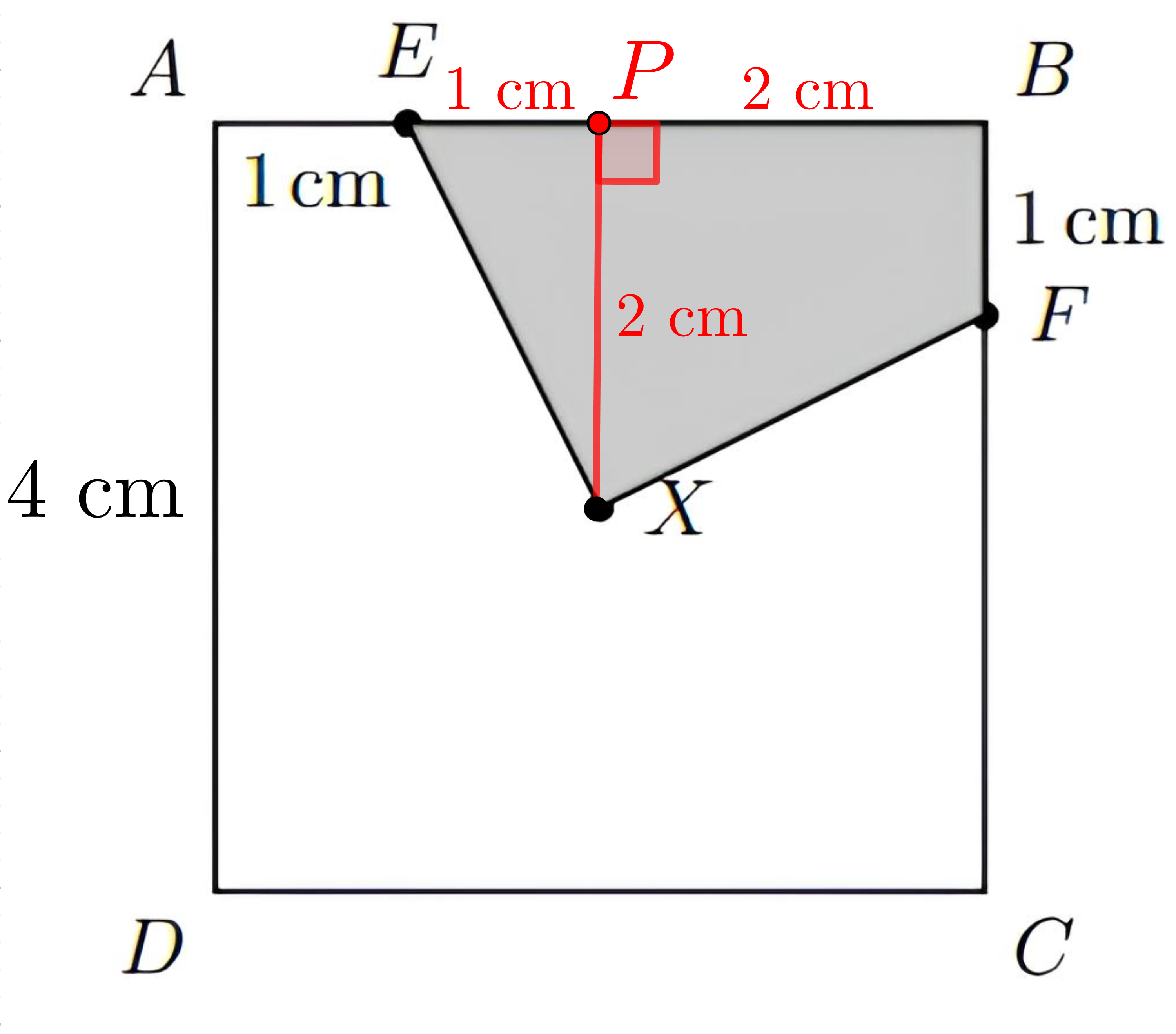
Assim, a área pedida é dada por
[tex]\qquad \dfrac{1\times 2}{2}+\dfrac{(1+2)\times 2}{2}=1+3=\boxed{4\text{ cm}^2}.[/tex]
Solução elaborada pelo COM Koreil Guys.
Solução 3
Nota: Nesta solução, a notação [tex][ABC\dots X][/tex] indica a área do polígono [tex]ABC\dots X[/tex].
Por simetria, é possível perceber que o quadrado [tex]ABCD[/tex] pode ser dividido em [tex]4[/tex] quadriláteros congruentes a [tex]XEBF[/tex] sempre que [tex]AE=BF[/tex]. Desse modo, a área [tex][XEBF][/tex] será dada por
[tex]\qquad [XEBF]=\dfrac{1}{4}[ABCD]=\dfrac{16}{4}=4\text{ cm}^{2}.[/tex]
Outra maneira de pensar é calcular a soma das áreas dos triângulos [tex]XEB[/tex] e [tex]XFB[/tex]:
[tex]\qquad [XEBF]=[XEB]+[XFB],[/tex]
[tex]\qquad[XEB]=\dfrac{3\cdot 2}{2}=3,[/tex]
[tex]\qquad[XFB]=\dfrac{1\cdot 2}{2}=1.[/tex]
Portanto,
[tex]\qquad[XEBF]=[XEB]+[XFB]=3+1=\boxed{4\text{ cm}^2}.[/tex]
Solução elaborada pelo COM Koreil Guys, com contribuições dos moderadores do Blog.
