|
E aí, o que você concluiu com relação aos exemplos 4 e 5, nos quais apareceram três escolhas: as três escolhas do ratinho e as três escolhas da Raíza? |
|
Observei um fato bem interessante! Em cada situação, as três escolhas puderam ser “agrupadas” em apenas duas e, então, foi possível aplicar o Princípio Multiplicativo! |
 |
 |
Bom, muito bom… |
Princípio Fundamental de Contagem – Generalização
Observe que, a partir do PFC , podemos raciocinar da seguinte forma
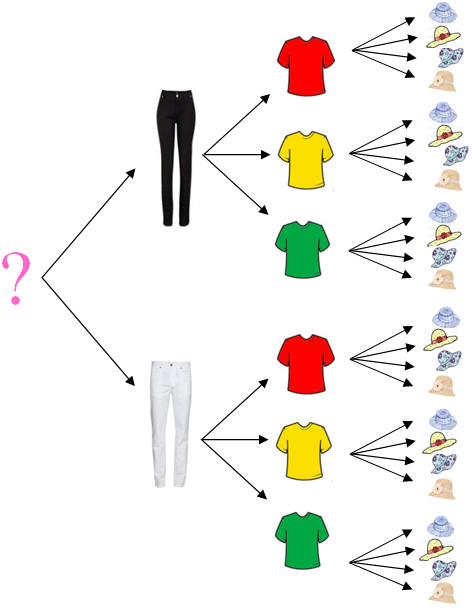
– temos, agora, duas decisões a serem tomadas: a escolha da roupa (calça e camiseta) e a escolha do chapéu.
Podemos calcular as possibilidades para a primeira escolha multiplicando o número de calças pelo número de blusas, como já fizemos. Essa multiplicação nos daria 6 possibilidades para a escolha da roupa.
Feito isso, utilizamos novamente o PFC para duas decisões (a escolha da roupa e a escolha do chapéu), e encontramos um total de 6 × 4 = 24 possibilidades.
Porém, se formos analisar essa solução vamos verificar que fizemos a multiplicação (2 × 3) × 4. Pela propriedade associativa da multiplicação, essa expressão equivale a 2 × 3 × 4, ou seja, à multiplicação das possibilidades individuais de cada uma das três escolhas: a escolha da calça, a escolha da camiseta e a escolha do chapéu.
Para cada calça, há 3 possibilidades de camiseta e, para cada conjunto com uma calça e uma camiseta, há 4 possibilidades de chapéu. Portanto, o número total de possibilidades de escolha para os modelitos de Raíza é (2 × 3) × 4 = 2 × 3 × 4 = 24.
Um raciocínio semelhante pode ser aplicado para problemas com quatro ou mais decisões. Sendo assim, o PFC pode ser enunciado de forma geral:
Princípio Multiplicativo – Princípio Fundamental da Contagem
Se as decisões A1, A2, A3, …, An puderem ser tomadas de, respectivamente, a1, a2, a3, …, an maneiras diferentes, então a quantidade de maneiras de se tomar sucessivamente essas n decisões é dada pelo produto: a1 × a2 × a3 × … × an.
|
Poxa, isso é muito legal! |
 |
 |
Os problemas a seguir são para você pensar: tente resolvê-los sem ver as soluções. |
Problemas Propostos
Problema 6:
Quantos são os números pares, de três algarismos, e começados por um algarismo ímpar?
Problema 7:
De quantas maneiras podemos escolher um chefe, um tesoureiro e um secretário para um clube, sendo que há 10 candidatos a chefe, 20 candidatos a tesoureiro e 30 candidatos a secretário?
Problema 8:
Cristina nasceu em um dia par, de um mês ímpar, de um ano par. Sabendo que ela nasceu após 1991 e antes de 2014, quantas são as possíveis datas para o nascimento de Cristina?
Problema 9:
De quantas maneiras podemos escolher um capitão, um imediato e um cozinheiro de bordo de uma tripulação composta por 15 homens?
Problema 10 (Banco de Questões – OBMEP 2011):
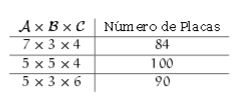
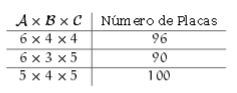
Cada uma das placas das bicicletas de Quixajuba contém três letras.
A primeira letra é escolhida dentre os elementos do conjunto A={G, H, L, P, R}, a segunda letra é escolhida dentre os elementos do conjunto B={M, I, O} e a terceira letra é escolhida dentre os elementos do conjunto C={D, U, N, T}.
Devido ao aumento no número de bicicletas da cidade, teve-se que expandir a quantidade de possibilidades de placas. Ficou determinado acrescentar duas novas letras a apenas um dos conjuntos ou uma letra nova a dois conjuntos.
Qual o maior número de novas placas que podem ser feitos, quando se acrescentam as duas novas letras?
Problema 11:
Ânika confecciona bolsas artesanais. Ela dispõe de 4 diferentes tipos de fecho, 3 diferentes tecidos para a bolsa e 6 cores distintas para a flor a ser utilizada como o “toque final”. Além disso, ela consegue fazer 2 modelos distintos de alça.
Ânika promete exclusividade a todas as suas clientes. No máximo quantas clientes poderão comprar de Ânika até que ela modifique suas disponibilidades?
|
Será que com o Princípio Multiplicativo dá para calcular quantas placas de automóveis pode haver no Brasil? |
 |
 |
Sim! |
|
Nossa, utilizando o Princípio a gente faz uma contagem, sem contar! |
 |
Equipe COM – OBMEP
 |
Esperamos que você tire proveito da explanação feita aqui. |
|
Reúnam seus Clubes, cliquem AQUI e |
 |