Malabarismos aritméticos e algébricos
Sala 1
|
O meu professor foi injusto comigo na correção de uma questão da minha última prova… |
 |
 |
Vamos ver se eu posso ajudar. |
|
Era só uma simplificação de fração! |
 |
 |
E a sua justificativa? |
[tex]\dfrac{16}{64}=\dfrac{1\cancel{6}}{\cancel{6}4}=\dfrac{1}{4}[/tex] |
 |
 |
Desculpe-me, mas o seu professor não foi injusto: a sua resolução está completamente errada! |

Uma das características da Matemática é o caráter incontestável de seus procedimentos e de suas conclusões. Assim, um procedimento matemático que acarrete um resultado correto, se repetido em condições análogas, deverá acarretar resultados corretos SEMPRE.
Simplificações como a mostrada na discussão inicial não podem ser consideradas como procedimentos matemáticos, já que, por exemplo, ao repetir esse tipo de cancelamento na fração [tex]\dfrac{20}{2}[/tex], obteríamos [tex]\dfrac{20}{2}=\dfrac{\cancel{2}0}{\cancel{2}}[/tex] e com isso estaríamos afirmando que [tex]10=\dfrac{20}{2}=\dfrac{\cancel{2}0}{\cancel{2}}=0[/tex], ou seja, que [tex]10=0[/tex].
|
Nooooooossaaaaa; é isso mesmo! |
 |
Assim como essa “simplificação de frações”, existem outros procedimentos incorretos que são feitos sistematicamente por muitos e muitos alunos. Dessa forma, abordaremos nesta sala algumas situações corriqueiras que os alunos vez por outra estão errando; além, é claro, de mostrar as formas corretas de se lidar com essas situações.
Então, vamos lá…
Alguns erros algébricos e aritméticos
|
Situação 1 |
|
|
[tex]5^3=15 \, ?[/tex]
|
Entenderam o cálculo que foi feito para determinar o valor de [tex]5^3[/tex]?
Pois é, galera, está e r r a d o ! O cálculo efetuado foi [tex]5\cdot 3=15[/tex] e isso não está certo. Este é um erro muito comum, vejam a forma correta de resolução: [tex]\qquad \qquad \boxed{5^3=5\cdot5\cdot 5=125}[/tex].
Por definição, potência de expoente inteiro positivo é o produto obtido pela multiplicação de fatores iguais, isto é, ao escrevermos [tex]a^b[/tex], com [tex]b[/tex] um inteiro positivo, devemos fazer o produto de [tex]b[/tex] fatores iguais a [tex]a[/tex].
Vejam: [tex]\qquad \qquad a^b= \underbrace{a\cdot a\cdot a\cdot \ldots \cdot a}_{b\ fatores}.[/tex]
|
|
Situação 2 |
|
|
[tex]\dfrac{7}{5}+\dfrac{2}{4}=\dfrac{9}{9}=1 \, ?[/tex]
|
Muito bem; se [tex]\dfrac{7}{5}+\dfrac{2}{4}=\dfrac{9}{9}=1[/tex], concluímos erradamente que [tex]1,4 + 0,5 = 1 \, [/tex]!
Na soma de frações não vale operar numerador com numerador e denominador com denominador. Isso vale apenas no produto de frações. Para a soma, devemos primeiro reduzir as frações ao mesmo denominador. Vejam: [tex]\qquad \boxed{\dfrac{7}{5}+\dfrac{2}{4}=\dfrac{7 \times 4}{5 \times 4}+\dfrac{2 \times 5}{4 \times 5}=\dfrac{28}{20}+\dfrac{10}{20}=\dfrac{38}{20}=\dfrac{19}{10}} \, [/tex].
De maneira geral, se [tex]a, \, b, \, c, \, d[/tex] são números inteiros, com [tex]b\ne 0 \, [/tex] e [tex] \, d\ne 0[/tex], então:
[tex]\qquad \qquad \dfrac{a}{b}+\dfrac{c}{d}=\dfrac{a \cdot d}{b \cdot d}+\dfrac{c \cdot b}{b \cdot d}=\dfrac{a \cdot d+c \cdot b}{b \cdot d} \, [/tex]. A utilização do mínimo múltiplo comum (MMC) dos denominadores pode ajudar, pois, em algumas situações, ao utilizarmos o MMC dos denominadores como o denominador comum, a fração resultante pode apresentar numerador e denominador menores, sem a necessidade de simplificações. Por exemplo, como [tex]mmc(4,6)=12 \, [/tex], podemos calcular a soma [tex]\dfrac{5}{6}+\dfrac{1}{4}[/tex] da seguinte forma: [tex]\qquad \qquad \dfrac{5}{6}+\dfrac{1}{4}=\dfrac{5 \times 2}{6 \times 2}+\dfrac{1 \times 3}{4 \times 3}=\dfrac{10}{12}+\dfrac{3}{12}=\dfrac{13}{12} \, [/tex]. Fazendo o produto dos denominadores, obteríamos que: [tex]\qquad \dfrac{5}{6}+\dfrac{1}{4}=\dfrac{5 \times 4}{6 \times 4}+\dfrac{1 \times 6}{4 \times 6}=\dfrac{20}{24}+\dfrac{6}{24}=\dfrac{20+6}{24}=\\ \qquad \dfrac{5}{6}+\dfrac{1}{4}=\dfrac{26}{24}=\dfrac{13}{12} \, .[/tex] Observe que, com a utilização do mínimo múltiplo comum (MMC) dos denominadores, obtivemos como resultado final uma fração irredutível, sem precisar fazer simplificações, como no segundo procedimento.
|
|
Situação 3 |
|
|
[tex]\dfrac{5^3}{5}= \, ?[/tex]
|
Por incrível que pareça, surge o seguinte erro, quando alguns alunos trabalham com divisão de potência:
[tex]\qquad \qquad \dfrac{5^3}{5}=\ ^3[/tex]. Pior ainda é quando, ao ser alertada que o cálculo está errado, a pessoa reconhece o erro e, ao consertá-lo, faz isso: [tex]\qquad \qquad \dfrac{ \, \, \, \ ^3}{ \, \, \, }[/tex] e argumenta que faltou o traço da fração! (Ainda bem que colocou o tracinho; assim, a queda do [tex]3[/tex] vai ser menor…) Parece engraçado; mas, com ou sem tracinho, é um erro grotesco! O correto é se fazer [tex]\qquad \qquad \boxed{\dfrac{5^3}{5}=\dfrac{5^3}{5^1}=5^{3-1}=5^2=25}[/tex].
O que a matemática garante é que se [tex]a, \, n, \, m[/tex] são números reais, com [tex]a \ne 0[/tex], então:
[tex]\qquad \qquad \dfrac{a^m}{a^n}=a^{m-n}[/tex].
|
|
Situação 4 |
|
|
[tex]\dfrac{\sqrt{2}}{2}= \, ?[/tex]
|
Dá para imaginar o que aconteceu com o número [tex]\dfrac{\sqrt{2}}{2}[/tex]?
Pois bem, foi isso mesmo que você imaginou: [tex]\qquad \qquad \dfrac{\sqrt{2}}{2}=\sqrt{ \, \, }[/tex] Sem palavras pra descrever isso.
Na realidade, não há nada que possamos fazer para simplificar esse número. Devemos, apenas, deixar a expressão como [tex]\dfrac{\sqrt{2}}{2}[/tex] e pronto. Se for necessária uma aproximação, podemos escrever [tex]\dfrac{\sqrt{2}}{2} \approx 0,707[/tex].
|
|
Situação 5 |
|
|
[tex]\sqrt{a^2+b^2}=a+b \, ?[/tex]
|
Esse é outro clássico exemplo de erro cometido por aí afora: [tex]\sqrt{a^2+b^2}=a+b[/tex].
Como uma regra matemática deve ser válida SEMPRE, é só substituir valores para [tex]a[/tex] e [tex]b[/tex] e observar o tamanho do desastre… Por exemplo, se [tex]a=3[/tex] e [tex]b=4[/tex], claramente vê-se que: [tex]\qquad \qquad \sqrt{3^2+4^2}\neq 3+4 \, [/tex], já que [tex]\qquad \qquad \boxed{\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5} \qquad[/tex] e [tex]\qquad\boxed{ 3+4=7}[/tex].
E quanto vale a expressão [tex]\sqrt{a^2+b^2}[/tex]?
Bom, [tex]\sqrt{a^2+b^2}=\sqrt{a \cdot a+b \cdot b} [/tex], ou seja, efetuamos as duas potências e depois somamos os produtos obtidos. Se a soma final for um quadrado perfeito, extraímos a raiz; caso contrário, fica como está…
Se for necessário, podemos obtemos uma aproximação
ou mesmo uma simplificação, quando possível:
|
|
Situação 6 |
|
|
[tex]\dfrac{3x}{2}+\dfrac{2x}{3} =\dfrac{9x+4y}{\cancel{6}}=9x+4y \, ?[/tex]
|
É uma tentação cortar o denominador, não é?
Pois não deve!!! É muito comum alguém cometer esse erro. Muitos alunos fazem isso quando estão aprendendo a operar algebricamente – afinal para que reduzir ao mesmo denominador, não é?
Mas o “corte” só pode ser feito quando você possui uma igualdade; pois, nesses casos, é como se estivesse “passando para o outro lado da igualdade multiplicando” …
Vejam um exemplo: [tex] \dfrac{3x}{2}+\dfrac{2y}{3}=5 \Leftrightarrow \dfrac{9x+4y}{6}=\dfrac{30}{6} \Leftrightarrow \dfrac{9x+4y}{\cancel{6}}=\dfrac{30}{\cancel{6}} \Leftrightarrow \\ \Leftrightarrow 9x+4y=30.[/tex]
|
|
Situação 7 |
|
|
[tex]\sqrt{4}=\pm 2 \, ?[/tex]
|
Esse erro é quase uma unanimidade…
Mil desculpas, mas [tex]\sqrt{4}=2[/tex], assim como [tex]\sqrt{9}=3[/tex], [tex]\sqrt{100}=10[/tex], [tex]\sqrt{4000000}=2000[/tex] etc.
Os símbolos e os conceitos da Matemática têm significados únicos, para que procedimentos que os envolvam tenham sempre o mesmo resultado. Particularmente, dado um número real [tex]a[/tex], com [tex]a \geqslant 0[/tex], chamamos de raiz quadrada de [tex]a[/tex] o único número real não negativo [tex]b[/tex] ([tex]b \geqslant 0[/tex]) tal que [tex]b^2=a[/tex]. Neste caso, o número [tex]b[/tex] é denotado por [tex]\sqrt{a}[/tex].
Assim, [tex]\sqrt{0}=0[/tex] e, se [tex]a[/tex] é um número real positivo, então [tex]\qquad \qquad ” \, b=\sqrt{a} \, ” \iff ” \, b \in \mathbb{R}, \, b\gt 0 \, [/tex] e [tex] \, b^2=a \, “[/tex]. Portanto, em [tex]\mathbb{R}[/tex], se uma raiz quadrada existe, ela é SEMPRE não negativa.
|
|
Situação 8 |
|
|
[tex]x^2=4 \Rightarrow x^2=2^2 \Rightarrow x=2 \, ?[/tex]
|
Esse erro é também um campeão de popularidade.
O correto é concluir que, em [tex]\mathbb{R}[/tex], se [tex]x^2=4[/tex], então [tex]x=2 \, [/tex] ou [tex] \, x=-2[/tex]. Bem, alguém que tenha entendido que [tex]\sqrt{4}=2[/tex] deve estar arrancando alguns fios de cabelo, neste momento …
Determinar os valores reais de [tex]x[/tex] para os quais [tex]x^2=4[/tex] não é a mesma coisa que determinar os valores reais de [tex]x[/tex] para os quais [tex]x=\sqrt{4}[/tex].
No segundo caso, de acordo com a Situação 7, sabemos que existe um único valor para [tex]x[/tex]: [tex]x=2[/tex]. Então, acompanhem a resolução do problema de se encontrar os valores de [tex]x[/tex] para os quais [tex]x^2=4[/tex]:
Com a argumentação acima, apenas garantimos que [tex]2[/tex] e [tex]-2[/tex] satisfazem a igualdade em questão. Faltaria garantir que esses são os únicos números reais tais que [tex]x^2=4[/tex]. Mas isso pode ser rapidamente garantido já que a equação [tex]x^2=4[/tex] é equivalente a [tex]x^2-4=0[/tex] e sabemos que uma equação do segundo grau tem, no máximo, duas raízes reais, não é?
|
|
Situação 9 |
|
|
[tex]2x=8 \Rightarrow x=8-2=6 \, ?[/tex]
|
Esse errinho é de doer…
Rapidamente observamos que a resposta [tex]x=6[/tex] não está correta, já que [tex]2\times 6=12 \, [/tex] e não [tex]8[/tex].
Se [tex]a[/tex] e [tex]b[/tex] são números reais tais que [tex]ax=b[/tex], então [tex]x[/tex] deverá ser o número que multiplicado por [tex]a[/tex] resulte em [tex]b[/tex]. Desse modo, [tex]x[/tex] é o quociente [tex]\dfrac{b}{a}[/tex], desde que [tex]a \neq 0.[/tex] Por exemplo,
[tex]\qquad \qquad 3x=21 \Leftrightarrow x=\dfrac{21}{3}=7[/tex] e, na situação em questão, [tex]\qquad \qquad 2x=8 \Leftrightarrow x=\dfrac{8}{2}=4[/tex]. Em particular, se [tex]a = 0[/tex], temos duas situações extremas quanto ao valor de [tex]x[/tex] na equação [tex]ax=b[/tex]:
|
|
Situação 10 |
|
|
[tex]3x+3=9 \Leftrightarrow 3x=9+3 \, ?[/tex]
|
Essa é outra situação comum, mas o procedimento está e r r a d o.
É importante observar que, em uma equação, sempre que “passarmos um elemento de um membro para outro”, devemos alterar a operação fazendo a inversa da operação considerada.
Lembremos que a operação inversa da adição é a subtração e vice-versa. A operação inversa da multiplicação é a divisão e vice-versa. Portanto, corretamente, a igualdade [tex] 3x+3=9[/tex] pode ser assim desenvolvida: [tex]\quad 3x+3=9 \Leftrightarrow 3x=9-3 \Leftrightarrow 3x=6 \Leftrightarrow x=\dfrac{6}{3}=2[/tex]
|
|
Situação 11 |
|
|
[tex](a \pm b)^2=a^2 \pm b^2 \, ?[/tex]
|
Esse tipo de erro é muito comum na Álgebra.
Na realidade, o correto é [tex]\qquad (a\pm b)^2=a^2 \pm 2ab +b^2[/tex].
Como se mostra isso?
Vejamos: [tex]\qquad\qquad \begin{align*} (a+b)^2& = (a+b)\cdot (a+b) \\&= a\cdot(a+b)+b\cdot(a+b) \\ &= a^2+ab+ba +b^2 \\ &=a^2+2ab +b^2.\end{align*}[/tex] e também [tex]\qquad\qquad \begin{align*} (a-b)^2& = (a-b)\cdot (a-b) \\&= a\cdot(a-b)-b\cdot(a-b) \\ &= a^2-ab-ba +b^2 \\ &=a^2-2ab +b^2.\end{align*}[/tex]
|
|
Situação 12 |
|
|
[tex](1+a)\cdot(1+b)=1+ab \, ?[/tex]
|
Outro erro que é bem comum.
Erro???? Sim, erro. Veja este exemplo: [tex]\qquad \qquad (1+2)\cdot(1+3)=3 \cdot 4=\boxed{12}[/tex] e [tex]\qquad \qquad 1+2\cdot 3=1+6=\boxed{7}[/tex]
Mas, qual é o resultado de [tex](1+a)\cdot(1+b)[/tex]?
Observe: [tex]\quad \begin{align*}(1+a)\cdot(1+b)&=1 \cdot(1+b) + a \cdot(1+b)\\ &=1+b+a+ab\,.\end{align*}[/tex] E???? E mais nada! [tex]\qquad \qquad (1+a)\cdot(1+b)=1+b+a+ab[/tex] e pronto!
|
|
Situação 13 |
|
|
[tex]\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{a+b} \, ?[/tex]
|
Esse é mais um erro clássico!
Uma forma correta de lidarmos com a expressão [tex]\dfrac{1}{a}+\dfrac{1}{b}[/tex] é reduzir as duas frações ao mesmo denominador.
Vamos lá? [tex]\qquad \qquad \dfrac{1}{a}+\dfrac{1}{b}=\dfrac{b}{ab}+\dfrac{a}{ab}=\dfrac{b+a}{ab}[/tex]. Assim, [tex]\qquad \qquad \dfrac{1}{a}+\dfrac{1}{b}=\dfrac{b+a}{ab}[/tex]. Como [tex]b+a=a+b[/tex], podemos ainda escrever que [tex]\qquad \qquad \dfrac{1}{a}+\dfrac{1}{b}=\dfrac{a+b}{ab}[/tex]. Conforme observamos na situação 2, em expressões numéricas, o MMC entre [tex]a \, [/tex] e [tex] \, b[/tex] poderá ajudar…
|
|
Situação 14 |
|
|
[tex]-3x\lt 7\iff x \lt-\dfrac{7}{3} \, ?[/tex]
|
Não, não e não!
As expressões [tex]-3x\lt 7 \, [/tex]e [tex] \, x\lt -\dfrac{7}{3}[/tex] não são equivalentes. Para se convencer disso, basta substituir valores. Por exemplo, fazendo [tex]x=1[/tex] é verdade que [tex]-3x=-3 \times 1=-3 \lt 7[/tex], mas não é verdade que [tex] \, x=1 \lt -\dfrac{7}{3}[/tex].
Quando lidamos com igualdades, podemos fazer uma mesma operação em ambos os membros sem muita preocupação.
No caso citado, se houvesse uma igualdade, poderíamos multiplicar ambos os membros por [tex]-\dfrac{1}{3}[/tex] e obter [tex]\qquad \qquad -3x=7\iff x=-\dfrac{7}{3}[/tex]. Contudo, ao multiplicarmos ambos os membros de uma desigualdade por um número negativo, é necessário inverter o sinal da desigualdade. Na situação citada, o correto seria: [tex]\qquad \qquad-3x \lt7\iff x \gt -\dfrac{7}{3}[/tex].
|
|
Situação 15 |
|
|
As expressões
[tex]\dfrac{7}{x-1} \lt \dfrac{9}{x-3} \, [/tex] e [tex] \, x \gt -6 [/tex] são equivalentes?
|
Alguém poderia argumentar que a “equivalência” em questão poderia ser assim obtida:
[tex]
mas, por outro lado,
Assim, temos, pelo menos, um valor de [tex]x[/tex] tal que a desigualdade [tex] \, x \gt -6 [/tex] é verdadeira, mas a desigualdade [tex]\dfrac{7}{x-1} \, [/tex] não o é.
Conforme observamos na Situação 14, ao multiplicarmos ambos os membros de uma desigualdade por um número negativo, é necessário inverter o sinal. Você pode estar se perguntado: mas onde na dedução feita no início da discussão multiplicamos uma desigualdade por um número negativo?
A resposta não é difícil: observe que as expressões [tex](x-1)[/tex] e [tex](x-3)[/tex] variam de sinal conforme [tex]x[/tex] varia e isso compromete a passagem [tex]\,\, \dfrac{7}{x-1} \lt \dfrac{9}{x-3} \iff 7(x-3) \lt 9(x-1)[/tex]. E o que fazer???? Bom, uma forma de contornar esse tipo de problema e, particularmente, resolver a nossa desigualdade sem erros é cumprir este roteiro: 1) Observar que [tex]\begin{align*}\dfrac{7}{x-1} \lt \dfrac{9}{x-3} &\iff \dfrac{7}{x-1} – \dfrac{9}{x-3} \lt 0 \\ & \iff \dfrac{7\cdot (x-3)-9 \cdot (x-1)}{(x-1)(x-3)} \lt 0\\ & \iff \dfrac{7x-21-9x+9}{(x-1)(x-3)}\\ & \iff\boxed{\dfrac{-2x-12}{(x-1)(x-3)} \lt 0}. \end{align*}[/tex] 2) Analisar, isoladamente, a variação de sinal das expressões [tex](-2x-12)[/tex], [tex](x-1)[/tex] e [tex](x-3)[/tex] 3) A partir das conclusões do item anterior, analisar o sinal da expressão [tex]\dfrac{-2x-12}{(x-1)(x-3)}[/tex], em função da variação de [tex]x[/tex].
Vamos lá? O item 1 já está pronto
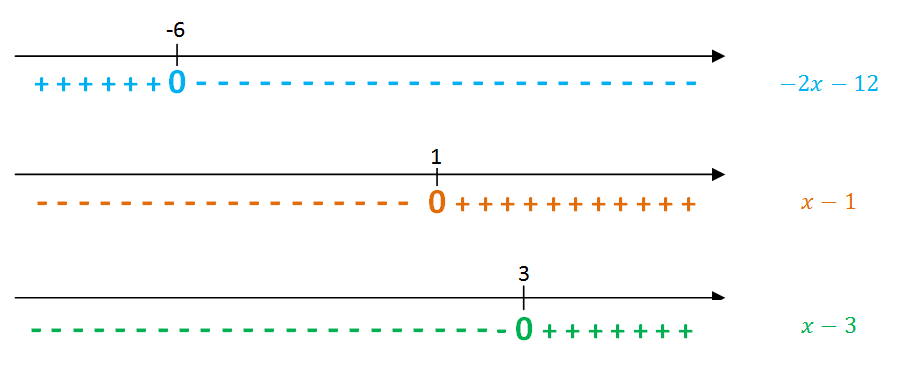
2) Análises isoladas de sinal
Analisar o sinal de [tex](-2x-12)[/tex] significa saber para que valores de [tex]x[/tex] a expressão define um número positivo, um número negativo ou o número [tex]0[/tex]. E não precisa adivinhar, é só fazer continhas…
[tex]\qquad -2x-12 \gt 0 \iff -2x \gt 12 \iff x\lt -6 [/tex] [tex]\qquad -2x-12 = 0 \iff -2x = 12 \iff x=-6 [/tex].
[tex]\qquad x-1 \gt 0 \iff x\gt 1 [/tex] [tex]\qquad x-1 = \iff x= 1 [/tex].
[tex]\qquad x-3 \gt 0 \iff x\gt 3 [/tex] [tex]\qquad x-3 = \iff x= 3 [/tex]. 3) A análise de sinal da expressão [tex]\dfrac{-2x-12}{(x-1)(x-3)}[/tex].
Esquematicamente:
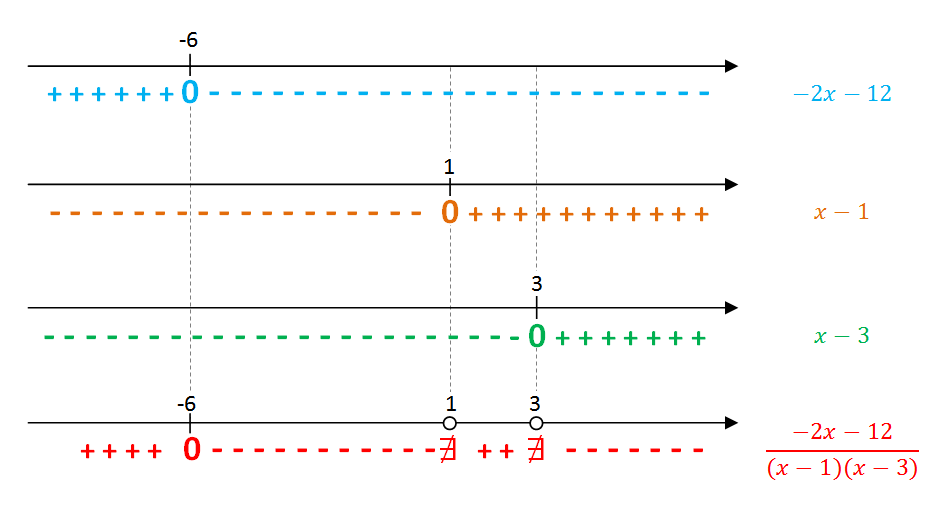
Lembrando das regrinhas de sinal para produtos e divisões:
podemos, finalmente, obter a variação de sinal da expressão [tex]\dfrac{-2x-12}{(x-1)(x-3)}[/tex]:
Como o item 1 nos garante que a solução da desigualdade [tex]\dfrac{7}{x-1} \lt \dfrac{9}{x-3} [/tex] são os valores de [tex]x[/tex] para os quais a expressão [tex]\dfrac{-2x-12}{(x-1)(x-3)}[/tex] é negativa.
Pergunta final: Não tem um jeito mais fácil de fazer isso?
|
Equipe COM – OBMEP