 |
Se você não se lembra ou não estudou o Teorema da Fatoração Única, clique AQUI! |
O método de fatoração que estudamos usualmente pode tornar-se inviável para números muito grandes, mesmo que utilizemos um computador potente. De fato, ainda não se conhece um algoritmo por meio do qual um computador possa fatorar números imensos em tempo hábil.
Só para vocês terem uma ideia, consideremos um número primo [tex]p[/tex] de [tex]47[/tex] algarismos. Assim, [tex]p \gt 10^{46}[/tex] e, portanto, [tex]\sqrt{p}\gt 10^{23}[/tex]. Pelo algoritmo tradicional de fatoração, aquele por tentativas, precisaríamos testar a divisibilidade de [tex]p[/tex] por todos os primos menores ou iguais à sua raiz quadrada. Há quase [tex]2\times 10^{21}[/tex] primos menores que [tex]10^{23}[/tex]. (Se você se interessou por essa informação, clique AQUI.) Para transformarmos essa informação em tempo de cálculo, precisamos ter uma ideia de quantas divisões um computador é capaz de efetuar em um segundo. Vejam só:
O supercomputador inaugurado pela USP em julho de 2015 faz algo em torno de [tex]4,6\times 10^{13}[/tex] operações por segundo. Se utilizássemos esse supercomputador para fazer as divisões, precisaríamos de aproximadamente [tex]\dfrac{2\times 10^{21}}{4,6\times 10^{13}}\approx 4,348\times10^{7}[/tex] segundos, o que equivale a mais de [tex]1[/tex] ano e [tex]4[/tex] meses.
 |
Se você achou que um ano e quatro meses é um tempo razoável para que sejam efetuadas [tex]2\times 10^{21}[/tex] divisões, tente calcular o tempo de se fazer, por exemplo, [tex]10^{40}[/tex] divisões . . .
|
Como fatorar números é uma questão central de segurança em alguns métodos de criptografia, além de ser, é claro, um problema fascinante, matemáticos de várias épocas têm se debruçado nesta questão e oferecido ao mundo novos métodos de fatoração, mais poderosos e, obviamente, menos naturais e menos conhecidos. Nesta Sala, apresentaremos um método que poderia ser classificado como pouco conhecido: a Fatoração por Fermat.
Vamos lá?
Fatoração por Fermat
Como dissemos na apresentação da Sala, o método comum de fatoração pode tornar-se inviável para números cujo menor fator primo é muito grande, mesmo utilizando um computador potente. Entretanto, o matemático francês Pierre de Fermat (1601-1665) desenvolveu um método muito eficaz para a fatoração de números que possuem um fator próximo à sua raiz quadrada. Este método ficou conhecido por Fatoração por Fermat.
Mesmo não sendo tão natural quanto o método de fatoração que já conhecemos, a Fatoração por Fermat não é um método difícil de ser compreendido, além de ser bastante interessante. Ele é a base para muitos dos poderosos métodos de fatoração que existem. Muito provavelmente, Fermat explicitou este método pela primeira vez em 1643, em uma carta endereçada ao matemático Marin Mersenne. Na suposta carta, Fermat teria fatorado o número [tex]2.027.651.281[/tex] utilizando esse método (Ver referência [4], p. 5).
Vejamos do que se trata.
O método
Seja [tex]n[/tex] o inteiro maior do que [tex]1[/tex] que queremos fatorar.
O objetivo do método que vamos apresentar é encontrar inteiros não negativos [tex]x[/tex] e [tex]y[/tex], [tex]x \gt y[/tex], tais que [tex]n=x^2-y^2.[/tex]
Mas por que isso nos ajudaria?
Sabemos que [tex]x^2-y^2=(x-y)(x+y)[/tex]; assim, se conseguirmos encontrar inteiros não negativos [tex]x[/tex] e [tex]y[/tex], com [tex]x>y[/tex], tais que [tex]n=x^2-y^2[/tex], então teríamos uma fatoração de [tex]n[/tex], não é? Não necessariamente em fatores primos; mas, se nenhum dos fatores [tex](x-y)[/tex] e [tex](x+y)[/tex] for [tex]1[/tex], teríamos a garantia de que [tex]n[/tex] é composto (obtemos uma decomposição de [tex]n[/tex] diferente de [tex]n=1\cdot n[/tex]), além de termos obtido uma ajuda na decomposição de [tex]n[/tex] em fatores primos. Assim,
demos um passo na direção certa!
Antes de estabelecermos como determinar efetivamente os inteiros não negativos [tex]x[/tex] e [tex]y[/tex], vamos fazer algumas observações.
- Para efeito de fatoração, podemos considerar que [tex]n[/tex] é um número ímpar; pois, do contrário, poderíamos escrever [tex]n=2^a \cdot b[/tex] para algum [tex]a[/tex] inteiro positivo e algum [tex]b[/tex] inteiro positivo ímpar. Como [tex]2[/tex] é primo, para fatorar [tex]n[/tex] como produto de primos bastaria conhecer a fatoração de [tex]b[/tex] e tudo recairia, então, no problema de se fatorar números ímpares.
Assim, de agora em diante, consideraremos que [tex]n[/tex] é um número ímpar maior do que [tex]1.[/tex] - Ao utilizarmos o processo que permitirá obtermos os inteiros não negativos [tex]x[/tex] e [tex]y[/tex], encontraremos números não inteiros. Como precisaremos trabalhar com números inteiros, utilizaremos a notação [tex][r][/tex] para indicar a parte inteira de um número real [tex]r[/tex]. Alguns exemplos:
● [tex][49]=49[/tex];
● [tex][2,3]=2[/tex];
● [tex]\left[\dfrac{234}{18954}\right]=0[/tex];
● [tex][\sqrt{2}]=[1,41…]=1[/tex];
● [tex][0,999…]=1[/tex]. (É [tex]1[/tex] mesmo!) - Se [tex]\sqrt{n}[/tex] for um inteiro positivo, então [tex]n[/tex] é um quadrado perfeito e, neste caso, o nosso trabalho de fatoração ficaria mais simples: como [tex]n=(\sqrt{n})^2[/tex], uma primeira fatoração de [tex]n[/tex] já estaria pronta.
(Para avançarmos em busca da fatoração de [tex]n[/tex] como produto de primos, precisaríamos nos concentrar apenas no inteiro positivo [tex]\sqrt{n}[/tex].)
A partir dessas três observações, estamos aptos a apresentar um processo sistemático que nos permitirá determinar inteiros não negativos [tex]x \, [/tex] e [tex] \, y[/tex] tais que [tex]x \gt y[/tex] e [tex]n=x^2-y^2.[/tex]
O algoritmo de fatoração de Fermat
Seja [tex]n[/tex] um inteiro ímpar maior do que [tex]1[/tex].
Passo 1
Calcule [tex]\sqrt{n}[/tex].
● Se [tex]\sqrt{n}[/tex] for um número inteiro, então o processo terminou, pois [tex]n[/tex] é um quadrado perfeito e basta, então, fazermos [tex]x=\sqrt{n}[/tex] e [tex]y=0[/tex].
● Se [tex]\sqrt{n}[/tex] não for um número inteiro, defina [tex]b=\left[\sqrt{n} \, \right][/tex] e vá para o Passo 2.
Passo 2
Faça [tex]x=b+1[/tex].
● Se [tex]x =\dfrac{n+1}{2}[/tex], então [tex]n[/tex] é primo, [tex]y=\sqrt{x^2-n}[/tex] e o processo terminou. Neste caso, observe que
[tex]\qquad \qquad y=\sqrt{x^2−n} = \sqrt{\left(\dfrac{n+1}{2}\right)^2−n} = \dfrac{n – 1}{2}[/tex].
● Se [tex]x \ne \dfrac{n+1}{2}[/tex], então vá para o Passo 3.
Passo 3
Calcule [tex]y=\sqrt{x^2-n}[/tex].
● Se [tex]y[/tex] for um número inteiro, então o processo terminou pois [tex]n[/tex] é composto e obtivemos inteiros não negativos [tex]x[/tex] e [tex]y[/tex] tais que [tex]x \gt y \, [/tex] e [tex] \, n=x^2-y^2.[/tex]
● Se [tex]y[/tex] não for um número inteiro, desconsidere o valor anterior de [tex] b[/tex], defina [tex]b=x[/tex] e volte para o Passo 2, redefinindo [tex]x[/tex] conforme este novo valor de [tex]b[/tex].
 |
Para quem não está habituado a trabalhar com algoritmos, preparamos alguns exemplos utilizando números conhecidos e pequenos, apenas para que todos entendam como funciona o Algoritmo de Fermat. |
Conhecidos o método e o algoritmo de Fermat, vamos analisar exemplos menos triviais.
|
Exemplo 4: Tome [tex]\boxed{n=323}[/tex] e observe que [tex]\boxed{{\color{blue}\dfrac{n+1}{2}= 162}}[/tex]. |
|
Passo 1: [tex] \sqrt{n}= \sqrt{323}\approx 17,97220[/tex]. |
|
Passo 2: Como [tex] x=b+1[/tex], então [tex]\boxed{x=18}[/tex]. |
|
Passo 3: Como [tex]y=\sqrt{x^2-n}[/tex], então [tex]\boxed{y=\sqrt{324-323}=1}[/tex]. |
|
Conclusão: O número [tex]323[/tex] é composto, [tex]\boxed{x=18} \, [/tex] e [tex] \, \boxed{y=1}[/tex]. |
No Exemplo 4, demos muita sorte! Se fôssemos utilizar o método comum de fatoração, teríamos um pouco mais de trabalho, não?
Antes de prosseguirmos, chamamos a atenção para a simplicidade dos passos que compõem o Algoritmo de Fermat. Na prática, para determinarmos se um dado número natural é primo ou composto, testamos, inicialmente, se ele é um quadrado perfeito. Em caso negativo, tentamos encontrar o menor valor inteiro positivo de [tex]x[/tex] tal que [tex]x \lt \dfrac{n+1}{2}[/tex] e para o qual a expressão [tex]y=\sqrt{x^2-n}[/tex] forneça um número inteiro. Para isso, partimos do valor inicial [tex]x=\left[\sqrt{n}\right]+1[/tex] e esse valor vai sendo incrementado de uma em uma unidade, até que [tex]x[/tex] seja igual a [tex]\dfrac{n+1}{2}[/tex] ou que [tex]y=\sqrt{x^2-n}[/tex] seja um número inteiro.
Usando essa observação, vamos a mais um exemplo: [tex]n=35659[/tex].
|
Exemplo 5:
● Como [tex][\sqrt{35659}][/tex] não é um inteiro, [tex]35659[/tex] não é um quadrado perfeito. |
Mas sabemos que [tex]169=13^2[/tex] (Exemplo 3) e, consultando uma tabela de primos, vemos que [tex]211[/tex] é primo, portanto a decomposição de [tex]35659[/tex] em fatores primos é [tex]35659=13^2\cdot 211[/tex]. Nada mal, não é mesmo?
Mas não se anime muito. Conforme dissemos lá em cima, este algoritmo só é assim tão rápido se houver um fator de [tex]n[/tex] não muito distante de [tex]\sqrt{n}[/tex]. Para descobrir que [tex]211[/tex] é primo utilizando esse mesmo algoritmo, por exemplo, seriam necessários mais de [tex]90[/tex] passos! Vocês se lembram de quantos passos fizemos nos exemplos 1 e 2?
Para comprovar, sem muito trabalho, que este método nem sempre é tão vantajoso, vamos fatorar [tex]n=2187[/tex] utilizando o algoritmo de Fermat e, depois, o algoritmo de fatoração que você já conhecia.
|
Pelo Algoritmo de Fermat… Observe, inicialmente, que [tex]\dfrac{n+1}{2}=\dfrac{2187+1}{2}={\color{blue} 1094}[/tex].
Como todos os valores utilizados para [tex]x[/tex] foram menores do que [tex] {\color{blue} 1094}[/tex] e [tex]y=27 \in \mathbb{Z}[/tex], então [tex]2187[/tex] é um número composto e tem como fatores Com isso, [tex]2187=3^4\cdot 3^3=3^7[/tex]. |
Pelo Método Tradicional de Fatoração…
Com apenas duas continhas, e mais simples que as anteriores, concluímos que [tex]2187[/tex] é composto e encontramos dois de seus fatores: [tex]3[/tex] e [tex]729[/tex]. |
Por que isso ocorreu?
Primeiro, porque [tex]n[/tex] é uma potência de um primo pequeno, a saber, [tex]3[/tex], e isso facilita bastante sua fatoração pelo método tradicional; segundo, porque seus fatores são [tex]1, 3, 9, 27, 81, 243, 729, 2187[/tex] e, sendo [tex]\sqrt{2187}\approx 47[/tex], não temos um fator tão próximo de [tex]\sqrt{2187}[/tex].
Muito bem, pelos poucos exemplos aqui apresentados, podemos intuir que, em alguns casos, o algoritmo de fatoração de Fermat é uma “mão na roda”. Mas precisamos de muito mais do que alguns exemplos para termos certeza de que ele sempre funciona. Para termos essa certeza, precisamos de respostas para algumas perguntas:
2) Nos casos em que [tex]n[/tex] for um inteiro composto ímpar, maior do que [tex]1[/tex], e não for um quadrado perfeito, sempre encontraremos um valor para [tex]x[/tex], com [tex][\sqrt{n}]+1\le x \lt \dfrac{n+1}{2}[/tex], tal que [tex]y=\sqrt{x^2-n}[/tex] seja inteiro e [tex]x-y[/tex] seja maior que [tex]1[/tex]?
3) Podemos ter certeza de que [tex]n[/tex] é primo se [tex]x[/tex] chegar a [tex]\dfrac{n+1}{2}[/tex]?
Sabemos que se o número a ser fatorado for um quadrado perfeito, o algoritmo termina no primeiro passo. Assim, note que, respondendo afirmativamente às perguntas 2 e 3, automaticamente responderemos à pergunta 1. Isso porque teremos a garantia de que, em cada processo de fatoração de números que não sejam quadrados perfeitos, executaremos um número finito de passos; já que, para cada um desses casos, existiria um número finito de inteiros [tex]x [/tex] tais que [tex][\sqrt{n}]+1 \le x \le \dfrac{n+1}{2}[/tex]. No entanto não são nada intuitivas as respostas às perguntas 2 e 3.
Mas, mantenham a calma, pois essas duas perguntas são respondidas positivamente e, assim, o Algoritmo de Fermat, embora muitas vezes muitíssimo trabalhoso de ser utilizado, funciona S E M P R E ! É claro que este algoritmo é muito mais poderoso e eficiente se implementado como um programa de computador.
Agora, se você quiser saber por que o algoritmo funciona sempre, é só clicar no botão Justificativas, abaixo, e você será levado a uma outra página, na qual encontrará o porquê das respostas afirmativas às perguntas 2 e 3. Mas se você quiser treinar um pouquinho, é só clicar no botão Problemas.
Para finalizar, um pouco sobre Criptografia.
Olhar digital – O que é criptografia
Pois é, nos dias de hoje, a criptografia não é mais utilizada somente para enviar mensagens secretas sem que o exército inimigo descubra! Ela não traz mais consigo a imagem de agentes secretos, mas sim a imagem da base de nosso mundo atual:
– precisamos proteger mensagens e transações realizadas pela Internet, incluindo transações financeiras!
Um dos mais importantes e bem sucedidos métodos de Criptografia é o método de Criptografia RSA, inventado em 1978 por Ron Rivest, Adi Shamir e Len Adleman, na época pesquisadores do Massachussets Institute of Technology (MIT).

Ron Rivest, Adi Shamir e Len Adleman
Entender este método é simples: escolhemos dois primos distintos, digamos [tex]p \, [/tex] e [tex] \, q[/tex], e calculamos o produto deles, digamos [tex]n=p \cdot q[/tex].
- Para se codificar (criptografar) uma mensagem, esta deve ser convertida em números, utilizando-se critérios específicos que fogem dos objetivos desta Sala: com isso a mensagem é convertida em blocos de números. Cada bloco numérico é submetido a uma cifragem na qual é utilizada como chave de codificação o produto [tex]n=p \cdot q[/tex]. Essa chave é pública, muitos a conhecem e ela pode, inclusive, ser obtida por meios ilícitos, como interceptações.
- Convertida a mensagem em código, é feito o envio.
- Recebida a mensagem codificada, apenas o destinatário legítimo (um Banco, por exemplo) deve ser capaz de decodificá-la (descriptografá-la), pois para isso é necessário conhecer os números [tex]p[/tex] e [tex]q[/tex] (por isso é que esses números precisam ser mantidos em segredo).
Assim, a segurança do método consiste basicamente no quão difícil é fatorar [tex]n[/tex]: quebrar o RSA consiste em obter os primos [tex]p[/tex] e [tex]q[/tex] (a chave privada), a partir do produto [tex]n=p \cdot q[/tex] (chave pública).
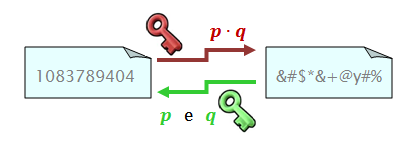
Os menos informados diriam que basta que os primos [tex]p[/tex] e [tex]q[/tex] sejam muito grandes (por exemplo, cada um com mais de [tex]100[/tex] algarismos) para melhorar a segurança do RSA; entretanto, conhecer a Fatoração por Fermat impõe outra condição: [tex]p[/tex] e [tex]q[/tex] não podem ser próximos da raiz quadrada do número [tex]n[/tex]… Neste caso, isso quer dizer que não podem ser próximos um do outro (consegue entender por quê?).
Caso tenha ficado curioso com este método de Criptografia, consulte as referências! Em particular, recomendamos a Apostila 7 do PIC.
Equipe COM – OBMEP
[1]COMUNICAÇÃO CEMEAI. Supercomputador será inaugurado em 14 de julho. (Último acesso em 14/06/20)
[2] COUTINHO, S. C., Criptografia. Rio de Janeiro: Impa, 2010. PIC Jr. da OBMEP – Apostila 7.(Último acesso em 14/06/20)
[3] COUTINHO, S. C., Números Inteiros e Criptografia RSA. 2. ed. Rio de Janeiro: Impa, 2014.
[4] KLEINER, Israel, Fermat: The Founder of Modern Number Theory. Mathematics Magazine, [s.l.], v. 78, n. 1, p.3-14, 1 fev. 2005. JSTOR.(Último acesso em 14/06/20)
[5] WIKIPÉDIA. TEOREMA DO NÚMERO PRIMO. (Último acesso em 14/06/20)
