Trigonometria do triângulo retângulo
Problemas
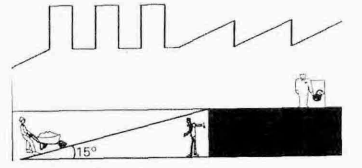
Para vencer um desnível de 4,25 metros vai ser construída uma rampa com inclinação de 15°.
Qual será o comprimento da rampa?
Problema 2:
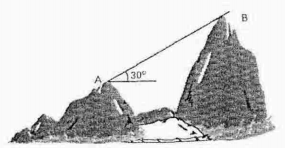
As alturas (em relação ao nível do mar) em que estão dois pontos A e B são, respectivamente, [tex] \, 812 \, m[/tex] e [tex] \, 1020 \, m[/tex]. Do ponto A vê-se o ponto B sob um ângulo de 30° com o plano horizontal, conforme a figura.
Determinar a distância entre os pontos A e B.
Quando o Sol está a 30° acima do horizonte, um edifício de 100 metros projeta uma sombra de quantos metros?
A quantos graus acima do horizonte deve estar o Sol para que um edifício projete uma sombra com o seu tamanho?
Do lugar onde me encontro, avisto uma torre segundo um ângulo de 32° com a horizontal.
Se me aproximo 25 metros da torre, o ângulo é de 50°.
Qual é a altura da torre?
Problema 6:
Se [tex]\theta_1, \, \theta_2, \, \theta_3[/tex] são ângulos agudos, calculem e completem a tabela abaixo, com valores aproximados.
| [tex]\theta_1[/tex] | [tex]\theta_2[/tex] | [tex]\theta_3[/tex] | |
| [tex]seno[/tex] | 0,87 | ||
| [tex]cosseno[/tex] | 0,14 | ||
| [tex]tangente[/tex] | 5,56 |
Uma escada de 3 metros está apoiada em uma parede.
Se o pé da escada está apoiado no chão a uma distância de 1,2 m da parede, qual a medida aproximada do ângulo que a escada forma com o chão?
O lado desigual de um triângulo isósceles mede 18 cm e a altura do triângulo relativa a este lado mede 10 cm.
Quais as medidas, em graus, dos três ângulos do triângulo em questão?
As tangentes a uma circunferência [tex]c[/tex] de centro [tex]O[/tex] e raio 12 cm, traçadas a partir de um ponto [tex]P[/tex] exterior a [tex]c[/tex], formam, entre si, um ângulo de 52°.
Qual a distância entre os pontos [tex]O \, [/tex] e [tex] \, P[/tex]?
Um avião está voando paralelo ao solo. Próximo do aeroporto, o avião inclina-se 30° e percorre 6 Km até tocar a pista de pouso.
A que altura ele estava voando?
Problema 11:
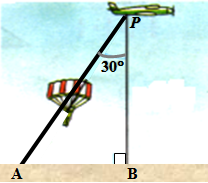
Um paraquedista salta de um avião quando este se encontra a 1.800 m de altura.
Devido à velocidade do avião e da ação do vento, o paraquedista salta do ponto [tex]P[/tex], mas cai no ponto [tex]A[/tex], conforme indica a figura.
A que distância do ponto B o paraquedista vai cair?
Problema 12:
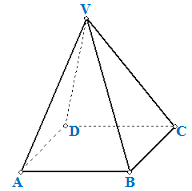
O lado da base de uma pirâmide quadrangular regular mede [tex]6 \, cm[/tex].
Se a medida do ângulo [tex]AVB[/tex] é [tex]60^{\circ}[/tex], qual é o volume da pirâmide?
Qual é a medida aproximada do ângulo que a diagonal de um cubo de aresta 8 cm forma com a diagonal de sua base?
Problema 14:
Existe algum ângulo de medida [tex]\theta[/tex], de sorte que [tex]sen \, \theta=\dfrac{3}{5}[/tex] e [tex]cos \, \theta=\dfrac{1}{4}[/tex]?
As igualdades abaixo vão verdadeiras?
[tex](i) \, (sen \, \theta+cos \, \theta)^2 + (sen \, \theta–cos \, \theta)^2 = 2[/tex]
[tex](ii) \, \dfrac{(sen \, \theta)^3+sen \, \theta \cdot (cos \, \theta)^2}{sen \, \theta}=1[/tex]
[tex](iii) \, \dfrac{(sen \, \theta)^3 + sen \, \theta \cdot (cos \, \theta)^2}{cos \, \theta}=tg \, \theta[/tex]
Um menino está a 2 m de uma parede.
Ao olhar para cima, ele vê o topo da parede sob um ângulo de 45° e, ao olhar para baixo, vê a base da parede sob um ângulo de 30°.
Qual é, aproximadamente, a altura dessa parede?
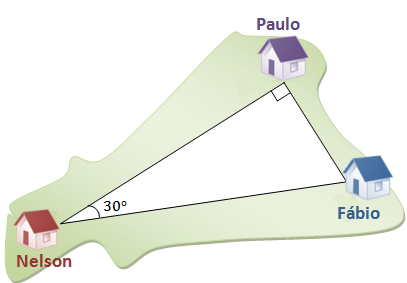
A figura mostra a disposição das casas de três amigos: Paulo, Nelson e Fábio.
Calcule, em metros, o comprimento de fio telefônico necessário para ligar a casa da chácara de Fábio à casa da chácara de Nelson, sabendo-se que foram gastos [tex]800 \, m[/tex] de fio para ligar a casa de Paulo à casa de Fábio.
Problema 18:
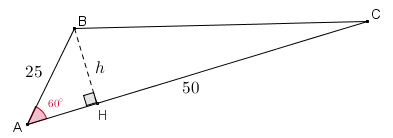
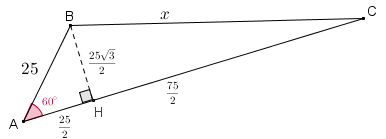
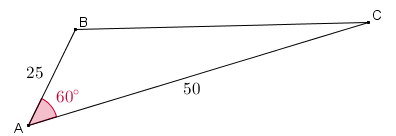
Podemos utilizar a trigonometria dos triângulos retângulos para resolvermos problemas cuja modelagem matemática utilize triângulos que não sejam retângulos. Por exemplo, qual é a distância entre os vértices [tex]B[/tex] e [tex]C[/tex] do triângulo abaixo? Pensem um pouquinho e, se não conseguirem resolver, é só clicar no próximo botão!
Equipe COM – OBMEP
✓ BIANCHINI, E.; MIANI, M., Construindo conhecimento em MATEMÁTICA – 8ª série. São Paulo: Moderna, 2000.
✓ IMENES, L. M.; LELLIS, M. Matemática para todos – 8ª série. São Paulo: Editora scipione, 2002.
✓ LEDUR, B. S.; ENRICONI, M. H. S.; SEIBERT, T. E. A, Trigonometria por meio da construção de conceitos. São Leopoldo: Unisinos, 2001.