Tópicos – Sala 2
VI – Pontos, segmentos de reta e circunferências
. . . em movimento
Com a Geometria Analítica podemos interpretar geometricamente equações ou, se preferirem, podemos expressar algebricamente, via equações, figuras geométricas – de qualquer modo, na Geometria Analítica figuras geométricas e equações andam de mãos dadas.
A maneira mais simples de vestir algebricamente objetos geométricos planos, por exemplo, começa por identificar um ponto [tex]P[/tex] de um plano qualquer com um par ordenado de números reais, [tex](x,y)[/tex]. Para tanto, fixamos no plano em questão o que chamamos na Matemática de eixos coordenados: dois eixos mutuamente perpendiculares que se intersectam num ponto [tex](0,0)[/tex]. Nesse caso, o plano munido dos eixos coordenados é denominado Plano Cartesiano, o ponto comum é denominado origem do plano, é denotado por [tex]O[/tex] (Não confundir com zero.) e é identificado com o par ordenado [tex](0,0)[/tex].
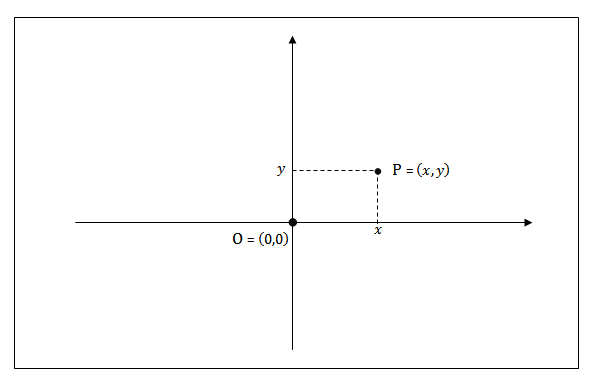 Até aí nada de novo, não é?
Até aí nada de novo, não é?
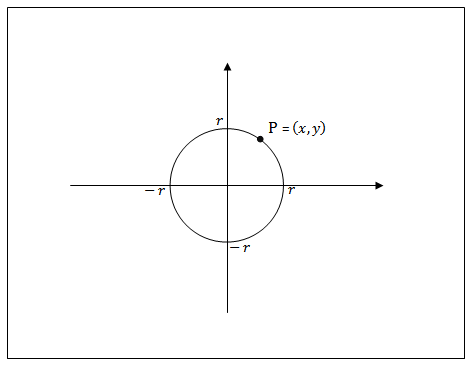
Assim como não é novidade o fato de que se um ponto [tex]P=(x,y)[/tex] está sobre uma circunferência de centro na origem de um sistema cartesiano e de raio [tex]r[/tex], então o teorema de Pitágoras nos garante que as coordenadas [tex]x[/tex] e [tex]y[/tex] satisfazem à equação [tex]x^2+y^2=r^2[/tex].
Essa conversa pode começar a se modificar se olharmos para a palavra GeoGebra e observarmos que:
- GeoGebra = GEOmetria + álGEBRA.
E se modifica de fato, se tentarmos utilizar o casamento da Geometria com a Álgebra e o GeoGebra para colocarmos a geometria em movimento. Vejamos alguns exemplos simples de como fazer isso.
Pontos em movimento
Na próxima figura podemos ver uma área de trabalho do GeoGebra na qual aparecem as duas janelas características do software: a Janela de Álgebra (à esquerda) e a Janela de Visualização (à direita).
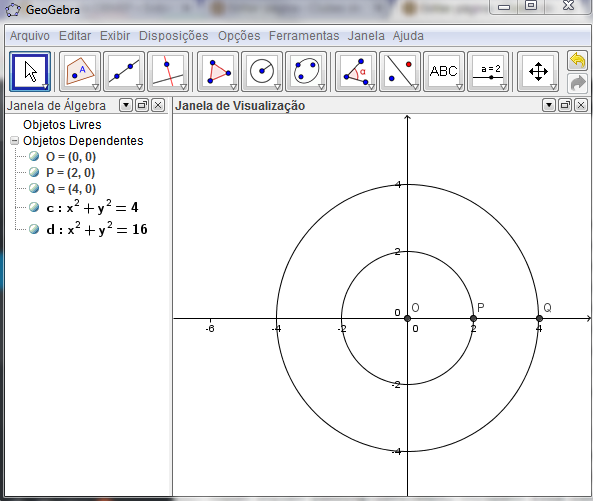
Observamos, então, o desenho e a equação de duas circunferências centradas na origem (indicadas por [tex]c[/tex] e [tex]d[/tex]), assim como os pontos [tex]O[/tex], [tex]P[/tex] e [tex]Q[/tex] e suas coordenadas.
Se clicarmos sobre o segundo ícone (da esquerda para a direita) na barra de ferramentas do GeoGebra e selecionarmos na janelinha que irá abrir a ferramenta Ponto em Objeto, poderemos, particularmente, criar um ponto sobre a circunferência de raio menor, bastando para isto clicar com o mouse sobre essa circunferência.
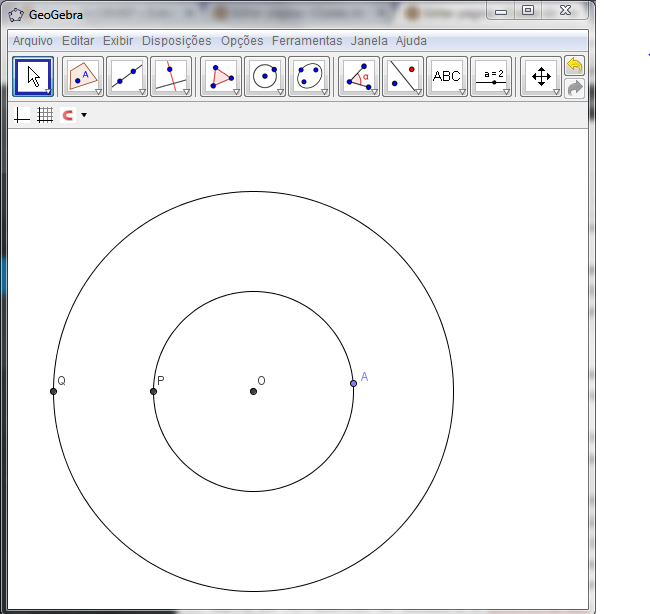
Na próxima figura, vemos o ponto A criado sobre a circunferência de raio [tex]2[/tex]. Observe que escondemos os eixos para uma melhor visualização, mas os objetos geométricos são os mesmos!
Mais ainda, o que acontecerá se clicarmos com o botão direito do mouse sobre o ponto criado e selecionarmos a opção Animar? Que tal um ponto em cada circunferência? E se ligarmos os dois pontos por meio de um segmento de reta?
Não é preciso que vocês façam um exercício de imaginação… Vejam:
Para parar a animação, cliquem no ícone || que aparece no canto inferior esquerdo do applet.
Observem que, na segunda animação, os pontos se movimentam sem que permaneçam alinhados com o centro da circunferência.
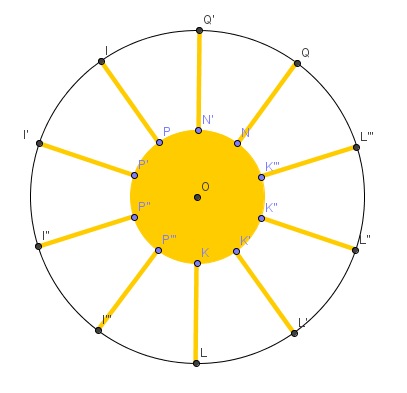
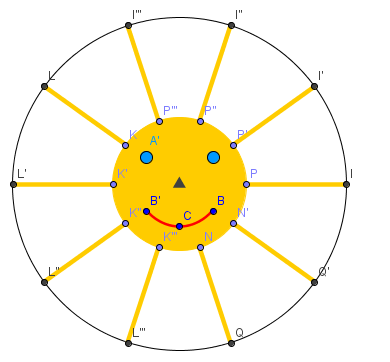
ATIVIDADE 5: Um sol em movimento
Utilizem as observações do tópico anterior e construam um sol em movimento.
Que tal um destes?
OBMEP_ srdg, criado com o GeoGebra
Para parar a animação, cliquem no ícone || que aparece no canto inferior esquerdo do applet.
Precisam de dicas?
VII – Maquinando
Embora simples, as ideias do tópico anterior permitem a construção de mecanismos mais elaborados com o GeoGebra. Neste tópico apresentaremos três objetos nos quais a geometria e o movimento estão presentes.
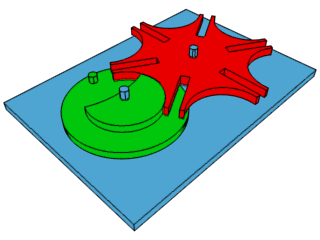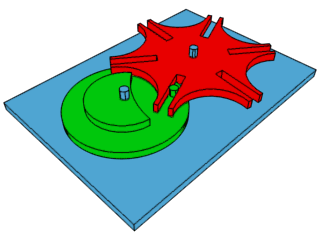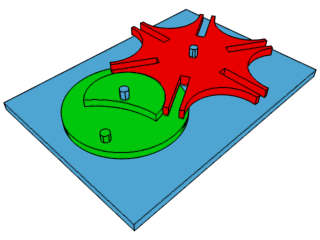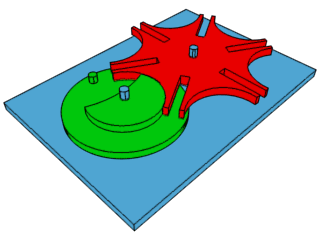
 Ventilador de teto |
 Macaco sanfona para veículos |
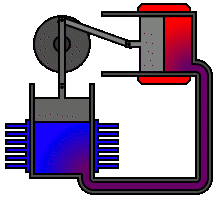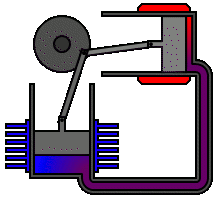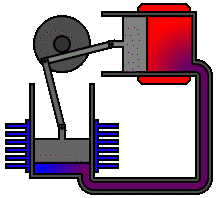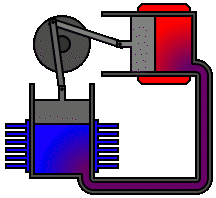
 Pistão |
Utilizando o GeoGebra, podemos construir modelos geométricos que permitam explorar o movimento desses objetos.
Cliquem nos respectivos botões para ter acesso à modelagem geométrica de cada mecanismo.
Grande parte do material utilizado neste tópico foi extraída do site Mídias Digitais I do Programa de Pós-Graduação em Ensino de Matemática, da Universidade Federal do Rio Grande do Sul.

VIII – Oficina de máquinas
Agora convidamos vocês para
construírem seus próprios mecanismos.
Assim, bom trabalho e boa diversão!
Grades pantográficas
Uma grade pantográfica é uma grade de segurança retrátil. Essas grades podem ser abertas e fechadas manualmente sempre que necessário, liberando assim a passagem através delas. Por serem mais pesadas que as grades fixas, elas fazem muito barulho ao serem manipuladas.
Esse tipo de mecanismo era comum em elevadores antigos, mas alguns prédios ainda mantêm portas pantográficas em seus elevadores. Em muitas residências também é possível encontrar esse tipo de grade em janelas e portas.
 Elevador com porta pantográfica de um edifício do centro de São Paulo.
Elevador com porta pantográfica de um edifício do centro de São Paulo.
Atividade 6
Construam no GeoGebra um mecanismo que simule uma grade pantográfica para um vão de 4 m x 2,5 m, de acordo com o modelo mostrado abaixo. Observem com cuidado os detalhes do modelo.
OBMEP_ srdg, criado com o GeoGebra
Precisam de ajuda para esta atividade? Cliquem no botão abaixo.
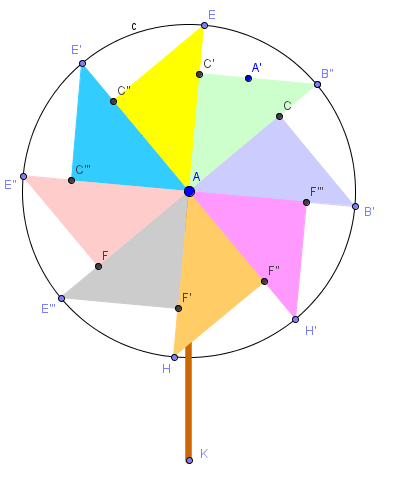
Cata-ventos
O cata-vento é um brinquedo que reproduz o movimento dos antigos moinhos de vento, que surgiram com a finalidade de moer grãos e outros alimentos, bombear água e hoje são utilizados até para produzir energia elétrica.
Ele funciona de maneira bastante simples: o vento passa entre suas “frestas” e o faz rodar.
Atividade 7
Construam no GeoGebra um mecanismo que simule um cata-vento rodando.
Vejam este modelinho:
OBMEP_ srdg, criado com o GeoGebra
Precisam de ajuda para esta atividade? Aí vão algumas dicas…
IX – Soltem a imaginação
soltem a imaginação……
Se vocês conseguirem modelar algum dos mecanismos, enviem para nós.
Teremos o maior prazer em divulgar o trabalho de vocês e ainda lhes enviaremos livros extras.
Então, vamos lá, pessoal!
Cliquem na figura correspondente ao vídeo que vocês querem assistir: na janela que irá abrir, é só clicar na setinha e, depois de assistir ao vídeo escolhido, é só fechar a janela que se abriu.
Equipe COM – OBMEP
➨ 100nexos (Último acesso em 15/08/18)
➨ GeoGebra (Último acesso em 15/08/18)
➨ Gif-Animados (Último acesso em 15/08/18)
➨ Licenças sob Domínio público via Wikimedia Commons
➨ Matthew DiVito – motion//graphic//design (Último acesso em 15/08/18)
➨ Wikipedia (Último acesso em 15/08/18)
➨ YouTube (Último acesso em 15/08/18)