Tópicos – Sala 1
I – Apresentação do Tema
O mundo que nos rodeia está repleto de situações em que a geometria se faz presente e em que formas geométricas se apresentam em movimento. Podemos perceber a geometria do movimento em diversas situações cotidianas, como no movimento das hastes de ventiladores, em pistões, macacos de carro, roldanas, janelas basculantes, escadas rolantes. E modelar “formas em movimento” é uma maneira de estudar geometria, pois propicia o desenvolvimento de conceitos e relações geométricas nelas presentes.
Portanto, a ideia desta proposta é apresentar, de forma breve, a construção de alguns “mecanismos” desenvolvidos com a ajuda da geometria dinâmica. Com esse objetivo, apresentaremos, então, exercícios exploratórios e proporemos a construção de duas curvas de considerável relevância no contexto histórico matemático. Como a geometria dinâmica será desenvolvida utilizando o GeoGebra, apresentaremos alguns dos recursos desse programa, a fim de que o manuseio desses recursos seja mais familiar e, consequentemente, vocês possam se aventurar, sem perigo, no estudo de um tema que, com certeza, é desconhecido por muitos.
Recheada com atividades, vídeos e materiais de apoio, além dos próprios objetos a serem desenvolvidos com o GeoGebra, essa dinâmica pretende servir como motivação para que os participantes sejam encorajados a desenvolverem seus próprios mecanismos, sejam concretos ou virtuais e, a partir desses, identificar o tanto de matemática que necessitamos para tal.
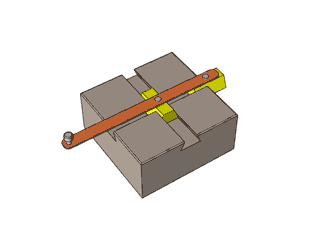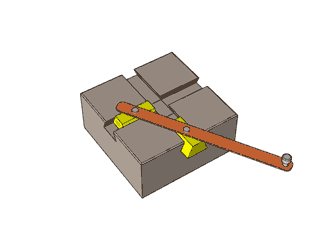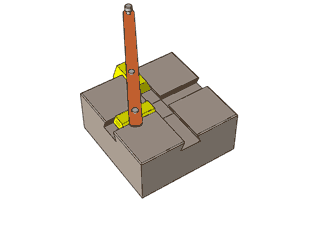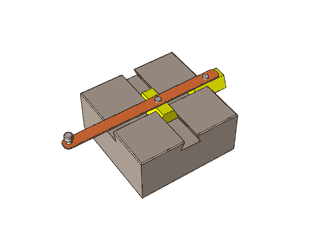
Olhem a construção abaixo…
Quem sabe um dia vocês não consigam produzir uma articulação sofisticada como esta, hein?
Para visualizar melhor, cliquem aqui.
E aí, animados? Então, visitem as próximas salas e
coloquem o corpo, a mente e a
geometria em MOVIMENTO!!!
II – Estruturas Rígidas
Para começar, antes de partirmos para articulações propriamente ditas, vamos discutir um pouco sobre estruturas rígidas.
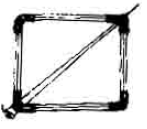
Você já reparou que, normalmente, nas porteiras de sítios ou fazenda temos uma estrutura como a apresentada abaixo? Você já pensou por que tem essa barra atravessada?

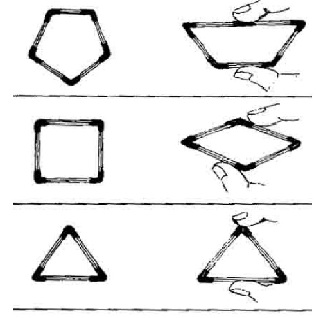
É simples… De modo geral, os polígonos são figuras deformáveis, ou seja, uma vez definidos seus lados, é possível alterar seus ângulos. Essas estruturas deformáveis podem ser transformadas em estruturas rígidas (não deformáveis), por meio de triângulos construídos a partir de alguns vértices do polígono.
Isso ocorre porque o triângulo é a única exceção entre os polígonos: uma vez definidos seus lados, não é possível alterar seus ângulos. Dizemos, então, que o triângulo tem uma estrutura rígida e é o único polígono rígido (não deformável).
Engenheiros, desde há muito tempo, sabem que sempre que eles precisarem de uma estrutura leve, forte e rígida, eles não têm escolha melhor do que as estruturas triangulares.
No vídeo que segue você verá uma animação que ilustra melhor a importância da triangulação em casos bem cotidianos, simulando, inclusive, as possíveis consequências em considerá-la ou não. O vídeo é um tutorial de um jogo (Bridge Constructor Playground) no qual o jogador terá que construir pontes sobre rios, canais ou vales. Depois de construídas, as pontes são submetidas a testes para ver se suportam o peso dos carros ou caminhões que irão utilizá-las. Embora o vídeo seja em inglês, vocês não terão dificuldades para entender as situações apresentadas.
ATIVIDADE 1
Chegou a hora de vocês praticarem um pouquinho…a ideia é que com essa atividade vocês possam:
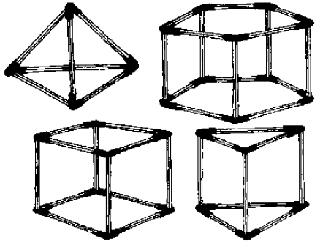
1) Construir figuras geométricas bi e tridimensionais;
2) Estudar estruturas rígidas utilizadas em construções;
3) Desenhar estruturas tridimensionais.
Material Necessário:
- Tripa-de-mico (encontrada em farmácias);
- Palito de Churrasco sem ponta;
- Tesoura;
III – Familiarizando-se com o GeoGebra
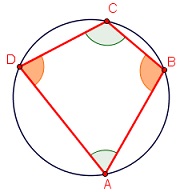
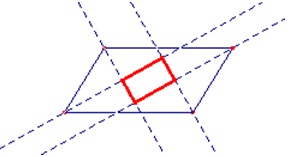
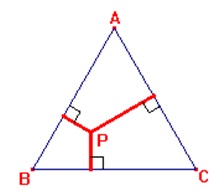
Agora que já conversamos um pouquinho sobre estruturas rígidas, propomos alguns exercícios exploratórios com triângulos e quadriláteros diversos, a fim de que possam ser evidenciadas algumas propriedades curiosas utilizando-se do recurso dinâmico. Mais do que isso, a intenção é que vocês possam se familiarizar com algumas ferramentas básicas do GeoGebra
ATIVIDADE 2
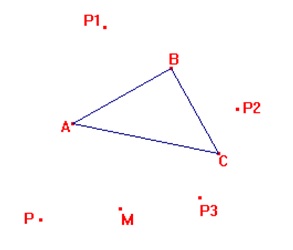
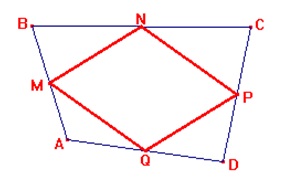
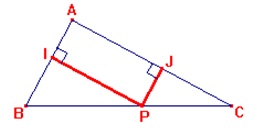
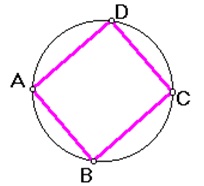
Escolham três dos exercícios abaixo e os resolvam com as devidas justificativas.
IV – Um primeiro mecanismo
Podemos utilizar o software GeoGebra para confeccionar mecanismos que estão no nosso dia a dia e obtermos instrumentos virtuais bem próximos do instrumento real que serviu como modelo.
Assim, que tal vocês aproveitarem as ferramentas do GeoGebra exploradas no tópico anterior para construírem um primeiro mecanismo?
Parece legal, não é?
Então libertem o Arquimedes e o Leonardo da Vinci que estão dentro de cada um de vocês e façam formas geométricas se movimentarem…
Bom trabalho, pessoal!
ATIVIDADE 3
1) Assistam ao vídeo a seguir.
2) Em seguida, procurem realizar a construção proposta, utilizando o GeoGebra.
Para ajudar, apresentamos o mecanismo resultante da atividade, em vídeo, para vocês. Mas a ideia é o desenvolvimento passo a passo do mecanismo das 4 barras.
V – A cicloide
Iniciamos este tópico com duas perguntas.
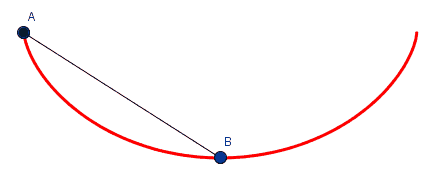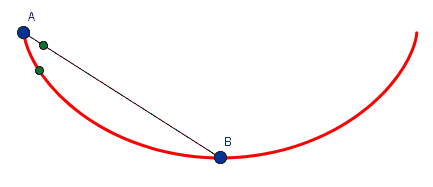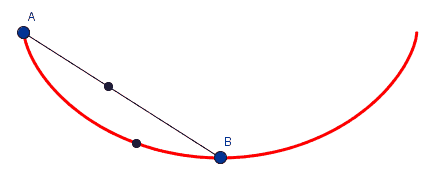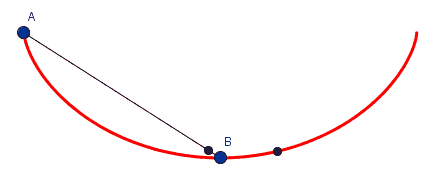
- Qual é a trajetória que uma partícula deve seguir em um plano vertical, para ir de um ponto mais alto até um ponto mais baixo desse plano, no menor espaço de tempo? De uma outra forma, qual a trajetória de descida mais rápida?
- É possível encontrar uma trajetória de modo que uma partícula atinja um ponto dado em um espaço de tempo que não dependa do ponto de onde ela saiu? De outra forma, é possível encontramos uma trajetória segundo a qual duas bolinhas soltas, simultaneamente, de alturas diferentes acabam por chegar ao mesmo tempo no ponto mais baixo dessa trajetória?
– Uma resposta intuitiva para a primeira pergunta seria uma trajetória retilínea, já que a menor distância entre dois pontos é o segmento de reta por eles definido.
– Para a segunda, a resposta intuitiva seria não, uma vez que a bolinha solta da menor altura atingiria o ponto mais baixo de uma trajetória primeiro.
As duas perguntas apresentadas são maneiras simples de tentarmos descrever dois famosos problemas matemáticos:
- o problema da Braquistócrona;
- o problema da Tautócrona.
e, contrariando a nossa intuição, veremos que o segundo problema tem solução e a trajetória retilínea não é a resposta do primeiro. Mais do que isso, veremos que a curva do menor tempo e a curva do mesmo tempo são, na verdade, a mesma!
A cicloide e um pouco de sua história
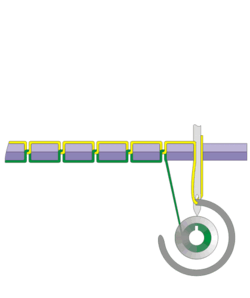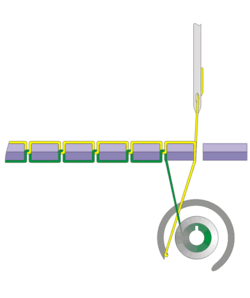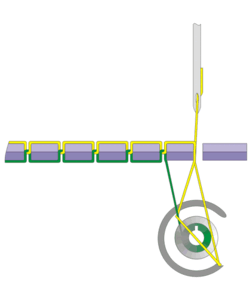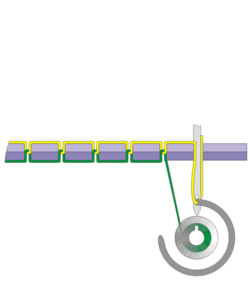
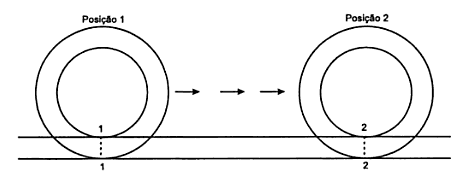
A cicloide é a curva descrita por um ponto de uma circunferência que roda sem deslizar ao longo de uma reta e tem propriedades bastante interessantes. 
Uma dessas propriedades é a resposta da primeira pergunta formulada neste tópico:
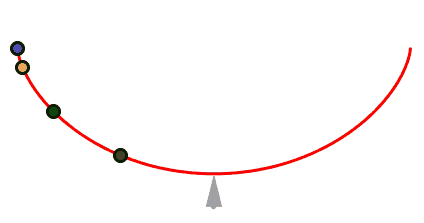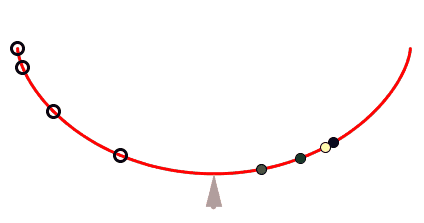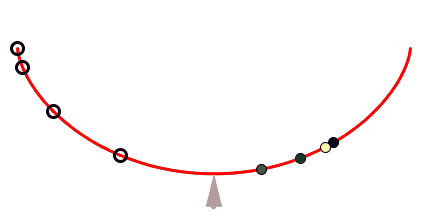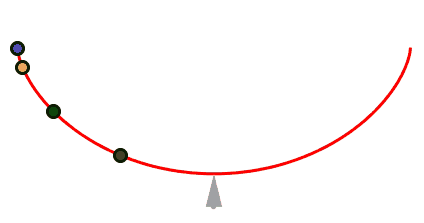
é a cicloide invertida a curva que une dois pontos distintos no menor tempo.
A segunda propriedade característica da cicloide é a resposta da segunda pergunta que formulamos neste tópico:
a cicloide invertida é a curva para a qual o tempo gasto por um objeto que por ela desliza, sem atrito, até seu ponto mais baixo independe do ponto de partida.
Aqui estão dois vídeos para ajudá-los no entendimento das duas propriedades da cicloide que apresentamos.
Cliquem na figura correspondente ao vídeo que vocês querem assistir: na janela que irá abrir, é só clicar na setinha e, depois de assistir ao vídeo escolhido, é só fechar a janela que se abriu.
A discussão matemática das soluções dos dois problemas apresentados fogem do objetivo desta Sala de Atividades, mas é importante ressaltar que esses problemas obrigaram os geômetras que com eles lidaram a raciocinar de maneira diferente, fazendo, então, surgir um novo ramo da matemática: o Cálculo Variacional.
Agora, que tal vocês se divertirem construindo e conhecendo melhor essa curva que, não só por suas belas propriedades mas também pelas várias disputas que gerou, ficou conhecida como a Helena da geometria?
Bom divertimento!
ATIVIDADE 4
Agora que vocês já construíram e se identificaram um pouco mais com a cicloide, prestem atenção na charada matemática a seguir e vejam se vocês são capazes de desvendá-la…
Se quiserem, podem tentar obter ajuda com o GeoGebra para melhor visualização. Façam um experimento concreto para convencerem-se se suas hipóteses estão corretas ou não. Procurem registrar o experimento em vídeo e apresentem junto com a solução. Juntem alguns pedaços de EVA, cola, durex, tesoura, caneta, transferidor…enfim, coloquem a criatividade em prática e mãos à obra…
Se vocês, ainda, não conseguiram resposta para a charada fiquem atentos e acompanhem no applet abaixo disponibilizado a construção sugerida. Quem sabe vocês não conseguem desvendar esse mistério…
Para melhor proveito, o applet abrirá em outra janela, é só clicar AQUI.
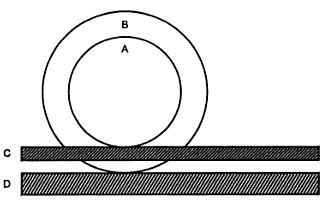
Será que essa construção é possível em uma situação concreta?
Em caso negativo, procure explicar com suas palavras, a partir de um experimento feito, o que o rolamento do círculo menor implicaria no maior (e vice-versa)?
Para encerrarmos este tópico dedicado à cicloide, vamos disponibilizar mais dois vídeos que podem ajudá-los de forma divertida com as discussões e atividades aqui apresentadas. Para assistir a um dos vídeos, basta clicar na figura correspondente e, na janela que irá abrir, é só clicar na setinha. Não se esqueçam de fechar a janelinha do vídeo, depois de assisti-lo.
Equipe COM – OBMEP
Janeiro de 2016.
➨ 100nexos (Último acesso em 15/08/18)
➨ GeoGebra (Último acesso em 15/08/18)
➨ Gif-Animados (Último acesso em 15/08/18)
➨ La cicloide y el péndulo de Huygens (Último acesso em 15/08/18)
➨ La Helena de la geometría (Último acesso em 15/08/18)
➨ Licenças sob Domínio público via Wikimedia Commons
➨ Matthew DiVito – motion//graphic//design (Último acesso em 15/08/18)
➨ Palpite digital (Último acesso em 15/08/18)
➨ Prof. Fagner Aguiar (Último acesso em 15/08/18)
➨ Wikipédia (Último acesso em 15/08/18)
➨ YouTube (Último acesso em 15/08/18)