Aplicando a matemática básica – Frações

Sônia foi à pizzaria com dois amigos: Paulo e Eduardo. Pediram uma pizza grande, que fora dividida em oito fatias iguais. Sônia comeu três das oito fatias, enquanto Paulo comeu uma e Eduardo comeu duas.

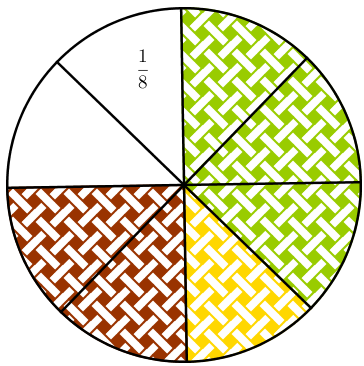
Como, então, representar as quantidades comidas pelos três em relação ao total da pizza? Vejamos:

► Sônia comeu três das oito fatias. Logo, ela comeu [tex]\dfrac{3}{8}[/tex] da pizza;
► Paulo comeu uma das oito fatias. Logo, ele comeu [tex]\dfrac{1}{8}[/tex] da pizza;
► Eduardo comeu duas das oito fatias. Logo, ele comeu [tex]\dfrac{2}{8}[/tex] da pizza;
► sobraram ainda duas das oito fatias. Logo, sobraram [tex]\dfrac{2}{8}[/tex] da pizza.

Assim, veja que para representar que parte da pizza cada um comeu e que parte da pizza sobrou é necessário utilizar números na forma de fração.
Isso seria útil, por exemplo, para criarem uma maneira de dividir os gastos, ou então para verificarem quanto dinheiro é gasto com o que sobrou ([tex]\frac{2}{8}[/tex] do preço total), decidindo se vale a pena comprar aquele tamanho de pizza da próxima vez ou não.

Os carros possuem em seu painel um medidor que registra a quantidade de combustível ainda disponível no tanque. Observe a figura que ilustra um modelo desse marcador.

Nesse modelo, no qual a letra V significa vazio e a letra C significa cheio, vejam que há três números na forma de fração [tex]\dfrac{1}{4}[/tex], [tex]\dfrac{2}{4}[/tex] e [tex]\dfrac{3}{4}[/tex]. Esses números são valores de referência; se, por exemplo, o tanque do carro tem capacidade para [tex]60[/tex] litros de combustível, então:

► se o ponteiro do mostrador estiver sobre a marcação [tex]\dfrac{1}{4}[/tex], então o tanque estará apenas com [tex]15[/tex] litros de combustível;
► já a segunda marcação, [tex]\dfrac{2}{4}[/tex], indica que, se o ponteiro do mostrador estiver sobre ela, então o tanque estará com a metade de sua capacidade total preenchida, ou seja, [tex]30[/tex] litros de combustível;
► finalmente, a terceira marcação, [tex]\dfrac{3}{4}[/tex], indica que, se o ponteiro do mostrador estiver sobre ela, o tanque estará com [tex]45[/tex] litros de combustível.

É muito comum, nos dias de hoje, ouvirmos frases como “a minha TV tem 40 polegadas”, ou “aquele monitor é de 29 polegadas”; mas nem todos sabem o que é essa tal de polegada…
A polegada é uma unidade de medida que foi criada na Inglaterra, no século XVI, pelo Rei Eduardo I, que teria medido o tamanho do seu próprio polegar, entre a base da unha e a ponta do dedo. Atualmente, a polegada é tomada como sendo 2,54 cm.

O Símbolo internacional para polegada é in; mas, geralmente, a unidade polegada é representada por uma dupla plica (″). Assim, as 40 polegadas da TV e as 29 polegadas do monitor citados podem ser assim representadas: 40″ , 40in; 29″ , 29in.

No Brasil, a polegada é também utilizada como unidade de medida de parafusos, tubulações e ferramentas e é bastante comum subdividir a polegada em meios, quartos e oitavos. Assim, é bastante comum encontramos frações expressando medidas em polegadas de vários objetos: [tex]\dfrac{1}{2}[/tex] polegada; [tex]\dfrac{3}{4}[/tex] de polegada; [tex]1 \frac{3}{4}[/tex] polegada (uma polegada e três quartos); [tex]2 \frac{1}{2}[/tex] polegadas (duas polegadas e meia).