Analisando injetividade e sobrejetividade de funções

Exemplo 1: Considere as seguintes funções:

[tex]\begin{array}{c|c|c|c}
f:\{-2,0,2\}\rightarrow\{0,4\}&g:\{0,2\}\rightarrow\{0,2,4\}&h:\{-2,0,2\}\rightarrow\{0,2,4\}&l:\{0,2\}\rightarrow\{0,4\}\\
\boxed{f(x)=x^2}&\boxed{g(x)=x^2}&\boxed{h(x)=x^2}&\boxed{l(x)=x^2}
\end{array}.[/tex]

Elas são injetoras? E sobrejetoras?
► Vamos explorar [tex]f, \, g, \, h, \, l \, [/tex] utilizando diagramas de Venn.

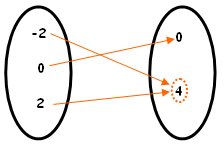
(a) [tex]f:\{-2,0,2\}\rightarrow\{0,4\}\\f(x)=x^2[/tex] Observem que a regra [tex]\boxed{ x \mapsto x^2}[/tex] está associando a dois elementos distintos, [tex]-2[/tex] e [tex]2[/tex], um único elemento, [tex]4[/tex]. Logo [tex]f[/tex] não é injetora. Observem também que os dois elementos do contradomínio são imagens, logo [tex]f[/tex] é sobrejetora.

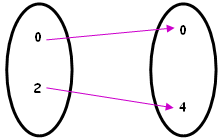
(b) [tex]g:\{0,2\}\rightarrow\{0,2,4\}\\g(x)=x^2[/tex] Observem que a regra [tex]\boxed{ x \mapsto x^2}[/tex] não está associando elementos ao número [tex]2[/tex] e, portanto, [tex]g[/tex] não é sobrejetora. Mas, por outro lado, elementos distintos do domínio têm imagens distintas, ou seja, [tex]g[/tex] é injetora.

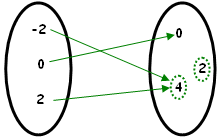
(c) [tex]h:\{-2,0,2\}\rightarrow\{0,2,4\}\\h(x)=x^2[/tex] Aqui, a regra [tex]\boxed{x \mapsto x^2}[/tex] está associando uma mesma imagem a elementos distintos e também não está associando elementos ao número [tex]2.[/tex] Com isso, [tex]h[/tex] não é injetora e nem sobrejetora.

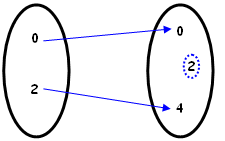
(d) [tex]l:\{0,2\}\rightarrow\{0,4\}\\l(x)=x^2[/tex] Aqui, a regra [tex]\boxed{x \mapsto x^2}[/tex] está apresentando simultaneamente as propriedades de injetividade e sobrejetividade. Assim, [tex]l[/tex] é uma bijeção.

IMPORTANTE: Notem que a regra [tex]x \mapsto x^2[/tex] provocou estruturalmente quatro situações distintas, pois com a mesma regra obtivemos funções com propriedades distintas:

• [tex]f[/tex] é uma função que não é injetora, mas é sobrejetora;
• [tex]g[/tex] é uma função que não é sobrejetora, mas é injetora;
• [tex]h[/tex] é uma função que não é injetora e nem sobrejetora;
• [tex]l[/tex] é uma função simultaneamente injetora e sobrejetora.

Dessa forma, percebam a importância de deixar claro qual é o domínio e qual é o contradomínio de uma função.

Exemplo 2: A partir de seus gráficos, verifique se as funções [tex]f,\,g,\,h,\,t\,[/tex] definidas de [tex]\{x \in \mathbb{R}~|~0\leqslant x \leqslant 5\}[/tex] em [tex]\mathbb{R}[/tex] são injetoras.

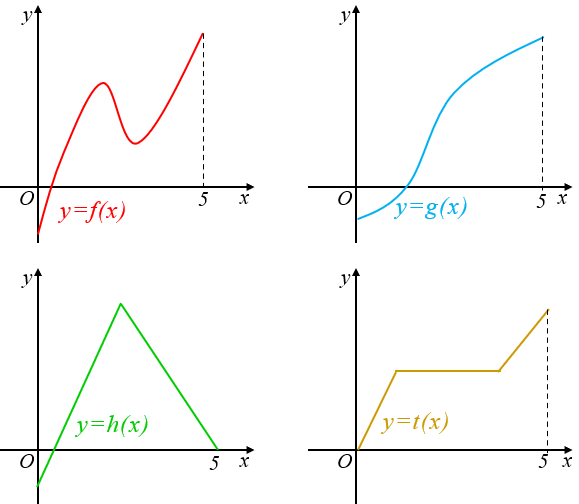
► Observem que existem retas horizontais que cruzam os gráficos das funções [tex]f,\,h,\,t\,[/tex] em mais de um ponto, conforme podemos observar na imagem a seguir. Mas qualquer reta horizontal cruza o gráfico da função [tex]g[/tex] em, no máximo, um ponto; abaixo podemos observar algumas dessas retas.

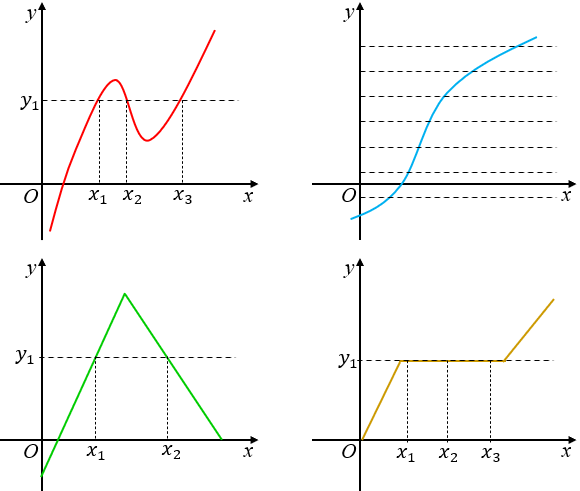
Dessa forma, podemos afirmar que apenas a função [tex]g[/tex] é injetora.

Exemplo 3: A partir de seus gráficos, verifique se as funções [tex]f,\,g,\,h,\,t\,[/tex] definidas de [tex]\{x \in \mathbb{R}~|~0\leqslant x \leqslant 5\}[/tex] em [tex]\{x \in \mathbb{R}~|~0\leqslant x \leqslant 6\}[/tex] são sobrejetoras.

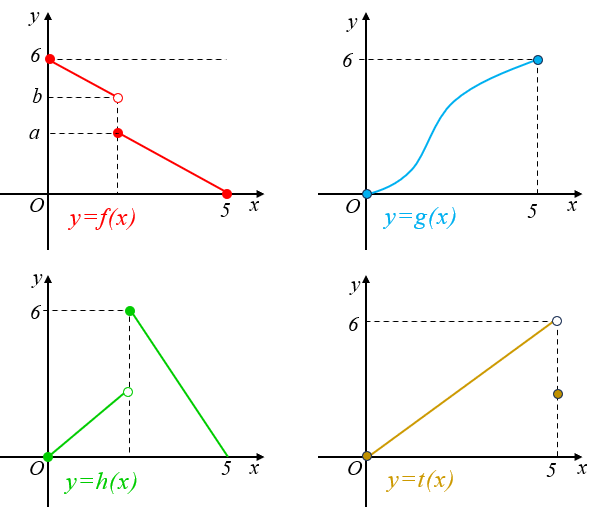
► Observem que no gráfico da função [tex]f[/tex] o intervalo [tex]]a,b][/tex] está contido no contradomínio da função mas nenhum elemento desse intervalo é imagem de elementos do domínio, logo [tex]f[/tex] não é sobrejetora.
► Todos os elementos do intervalo [tex][0,6][/tex] são imagens de elementos do domínio de [tex]g[/tex]; logo, essa função é sobrejetora.
► Todos os elementos do intervalo [tex][0,6][/tex] também são imagens de elementos do domínio de [tex]h[/tex]; logo, essa função é sobrejetora.
► Perceba que [tex]6\in [0,6][/tex] mas [tex]6[/tex] não é imagem de nenhum elemento do [tex]D(t)[/tex]. Assim [tex]t[/tex] não é uma sobrejeção.

Exemplo 4: Defina um contradomínio para a função [tex]f[/tex], definida em [tex]\mathbb{R}[/tex], cujo gráfico aparece abaixo, de modo que [tex]f[/tex] seja sobrejetora.

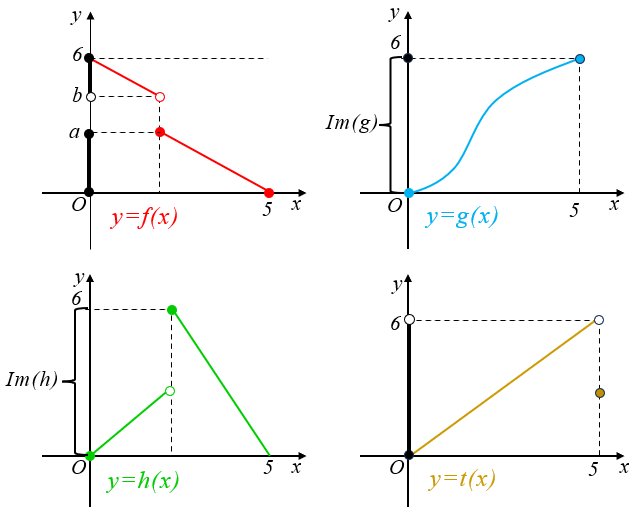
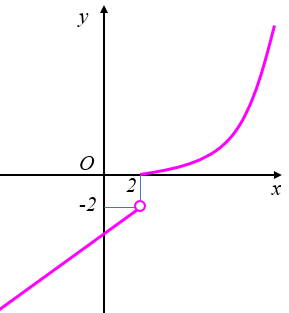
► Note que o conjunto imagem da função [tex]f[/tex] pode ser assim definido:
[tex]\qquad \qquad Im(f)=\,\left]-\infty\,,\,-2\right[\, \cup \,\left[0\,,\,+\infty\right[.[/tex]
Dessa forma, se [tex]CD(f)=\,\left]-\infty\,,\,-2\right[\, \cup \,\left[0\,,\,+\infty\right[[/tex], [tex]f[/tex] será sobrejetora.

Exemplo 5: (Ufpe) Sejam [tex]A[/tex] e [tex]B[/tex] conjuntos com [tex]m[/tex] e [tex]n[/tex] elementos, respectivamente. Verifique se as seguintes afirmações são verdadeiras ou falsas:
(i) Se [tex]f:A\rightarrow B[/tex] é uma função injetora então [tex]m\leqslant n.[/tex]
(ii) Se [tex]f:A\rightarrow B[/tex] é uma função sobrejetora então [tex]m\geqslant n.[/tex]
(iii) Se [tex]f:A\rightarrow B[/tex] é uma função bijetora então [tex]m=n.[/tex]
(iv) Se [tex]f:A\rightarrow B[/tex] é uma função bijetora então o gráfico de [tex]f[/tex] é um subconjunto de [tex]A \times B[/tex] com [tex]m\times n[/tex] elementos.
(v) Se [tex]m=n[/tex] o número de funções bijetoras [tex]f:A\rightarrow B[/tex] é [tex]m!\,.[/tex]

► Apenas a afirmação (iv) é falsa!