Clique no botão abaixo para visualizar a Sala.
Por exemplo, imagine que você irá ao supermercado para comprar, digamos, sete refrigerantes para uma festa de aniversário e há apenas três opções de sabores disponíveis. De quantos modos essa compra pode ser feita?
 Imagem extraída de Freepik
Imagem extraída de Freepik
Para resolver esse, e outros problemas semelhantes, esta Sala de Estudo aborda uma técnica de contagem um pouco mais sofisticada e conhecida como Combinação Completa (ou Combinação com Repetição).
Provavelmente, você já deve ter estudado a Combinação Simples.
De modo geral, essa técnica expressa o número de maneiras de escolhermos [tex]p[/tex] objetos distintos entre [tex]n[/tex] objetos distintos disponíveis, com [tex]n\geq p.[/tex]
Grande parte dos livros didáticos representa esse número por [tex]~C_{n}^{p}~[/tex] ou [tex]\;C_{n,p}\;[/tex] ou ainda [tex]\,\left(\begin{array}{c}n\\p\end{array}\right)\,[/tex], e esta combinação é calculada por
[tex]\qquad \qquad C_{n}^{p}=C_{n,p}=\left(\begin{array}{c}n\\p\end{array}\right)=\dfrac{n!}{p!\cdot(n-p)!}[/tex].
Já a Combinação Completa expressa o número de modos de escolher [tex]p[/tex] objetos distintos ou não entre [tex]n[/tex] tipos de objetos distintos dados. Para usarmos uma notação diferente, representaremos esse número por [tex]CR\,_{n}^{p}[/tex].
E como vamos calcular esse número?
Voltemos ao nosso exemplo inicial…
Vamos interpretar esse problema da seguinte forma:
Chamemos de [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] as quantidades que iremos comprar do primeiro sabor, do segundo sabor e do terceiro sabor, respectivamente. Note que [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] devem ser números inteiros não negativos e que [tex]A+B+C=7[/tex].
Daí, comprar [tex]7[/tex] refrigerantes em um supermercado que oferece [tex]3[/tex] sabores diferentes é encontrar uma solução, com inteiros não negativos, para a equação [tex]\boxed{A+B+C=7}\,.[/tex]
Vamos listar algumas soluções para essa equação:
- [tex]A=3[/tex], [tex]B=1[/tex] e [tex]C=3[/tex]
- [tex]A=7[/tex], [tex]B=0[/tex] e [tex]C=0[/tex]
- [tex]A=0[/tex], [tex]B=4[/tex] e [tex]C=3[/tex]
- [tex]A=1[/tex], [tex]B=2[/tex] e [tex]C=4[/tex],
mas observamos que há várias outras.
Para que não haja a necessidade de enumerar exaustivamente todas as soluções dessa equação, ao imaginarmos uma possível solução iremos representá-la no esquema bola-traço.
► A ideia é desenhar bolas idênticas (●), alinhadas horizontalmente, para representar os objetos que serão distribuídos, e separá-las em regiões, de acordo com a quantidade de incógnitas, utilizando traços (│):
– a quantidade de bolas será igual à soma das incógnitas, para que cada bola represente uma unidade no valor da incógnita;
– a quantidade de traços será uma unidade a menos que a quantidade de incógnitas, para que cada traço separe duas incógnitas.
A próxima imagem mostra as quatro soluções anteriores no esquema bola-traço.
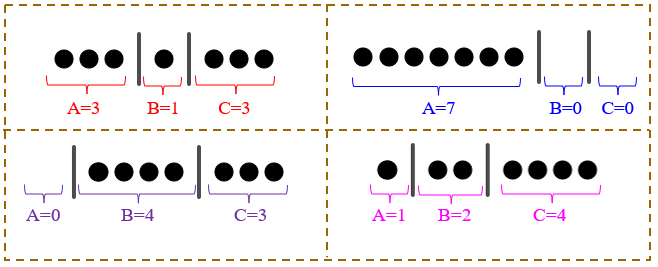
Assim, qualquer solução da equação [tex]\boxed{A+B+C=7}[/tex] nas condições do problema pode ser representada por uma fila com [tex]9[/tex] elementos: [tex]7[/tex] bolas (pois em cada solução devemos ter [tex]7[/tex] unidades distribuídas nas incógnitas) e [tex]2[/tex] traços (para separar três incógnitas usamos [tex]2[/tex] traços).

O total de filas com essa característica pode ser calculado utilizando a ideia de permutação com elementos repetidos.
Assim, o número de permutações de [tex]n[/tex] objetos dos quais um primeiro objeto se repete [tex]r_1[/tex] vezes; um segundo objeto se repete [tex]r_2[/tex] vezes; um terceiro, [tex]r_3[/tex] vezes; e assim sucessivamente até esgotar as repetições, com o objeto [tex]m[/tex] se repetindo [tex]r_m[/tex] vezes; é denotado por [tex]\,P_{n}^{r_1, \, r_2,\, r_3,\, \cdots, \, r_m}\,[/tex] e assim definido:
Logo, o número total de filas do nosso problema é dado por uma permutação com elementos repetidos; [tex]9[/tex] elementos, sendo [tex]7[/tex] bolas e [tex]2[/tex] barras:
[tex]\qquad P_{9}^{7,2}=\dfrac{9!}{7! \cdot 2!}=36.[/tex]
Observe que [tex]\, P_{9}^{7,2}=\dfrac{9!}{7! \cdot 2!}=C_{9}^{7}[/tex]; assim, de acordo com a notação definida para uma combinação completa, temos que:
[tex]\boxed{CR\,_{3}^{7}=P_{9}^{7,2}=C_{9}^{7}=\dfrac{9!}{7! \cdot 2!}=36}.[/tex]
Vejamos um outro exemplo de como encontrar o número de soluções inteiras não negativas de uma equação linear.
Aqui estão algumas soluções:
- [tex]x_{1}=1[/tex], [tex]x_{2}=1[/tex], [tex]x_{3}=3[/tex] e [tex]x_{4}=0[/tex];
- [tex]x_{1}=2[/tex], [tex]x_{2}=1[/tex], [tex]x_{3}=1[/tex] e [tex]x_{4}=1[/tex];
- [tex]x_{1}=0[/tex], [tex]x_{2}=5[/tex], [tex]x_{3}=0[/tex] e [tex]x_{4}=0[/tex];
e suas respectivas representações no esquema bola-traço.

Dessa forma, qualquer solução da equação pode ser representada por uma fila com [tex]8[/tex] elementos: [tex]5[/tex] bolas e [tex]3[/tex] traços.
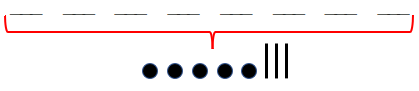
Logo, o número total de filas é:
[tex]\qquad \qquad P_{8}^{5,3}=\dfrac {8!}{5! \cdot 3!}=C_{8}^{5}=56[/tex],
número esse que representamos por: [tex]\boxed{CR\,_{4}^{5}=56}.[/tex]
O importante nesses dois exemplos é percebemos que podemos interpretar [tex]CR\,_{n}^{p}[/tex] de duas maneiras:
- [tex]CR\,_{n}^{p}[/tex] é o número de modos de selecionar [tex]p[/tex] objetos, diferentes ou não, entre [tex]n[/tex] objetos distintos dados;
- [tex]CR\,_{n}^{p}[/tex] é o número de soluções inteiras não negativas da equação [tex]x_{1}+x_{2}+\dots+x_{n}=p[/tex];
e que para calcular o número de soluções podemos utilizar o esquema bola-traço.
Portanto,
[tex]\qquad \qquad CR\,_{n}^{p}=P_{p+n-1}^{p, n-1}= \dfrac{(p+n-1)!}{p! \cdot (n-1)!}=C_{n+p-1}^{p}[/tex].
É importante observar que, quando utilizamos Combinações Simples de [tex]n[/tex] elementos tomados [tex]p[/tex] a [tex]p[/tex], devemos ter [tex]\boxed{~p \le n~}[/tex]. No entanto, tal restrição não se faz necessária no caso de Combinações com Repetição.
Vamos diferenciar as duas situações com um exemplo simples: a escolha de três letras dentre as letras A e B.
- Não tem sentido usar combinação simples para determinar quantas escolhas são possíveis neste exemplo, já que nesse tipo de combinação não podemos repetir elementos. Dessa forma, não temos como apresentar escolhas com três elementos distintos, se só dispomos de dois tipos de letras.
- No entanto, podemos utilizar combinação com repetição para quantificarmos as possíveis escolhas, uma vez que podemos repetir elementos na escolha de três letras dentre os dois tipos de letras apresentados:
Cálculo: [tex]CR\,_{2}^{3}=P_{4}^{3, 1}= \dfrac{4!}{3! \cdot 1!}=4[/tex];
Escolhas: AAA ; AAB ; ABB ; BBB.
Um vídeo para ajudar. . .
Assista ao vídeo abaixo para melhorar o seu entendimento e ampliar o seu conhecimento!
É só clicar na setinha.
Análise Combinatória – Combinação Completa
Vídeo extraído do Portal da Matemática – Professor Josimar Silva
O objetivo principal desta Sala não é a notação em si (mesmo sabendo de sua importância), mas sim resolver problemas de contagem utilizando essa nova técnica. Mas, antes, lembre-se de que:
► [tex]~\boxed{C_{n}^{p}=\dfrac{n!}{p!\cdot(n-p)!}}~[/tex] é o número de maneiras de escolhermos [tex]p[/tex] objetos distintos em [tex]n[/tex] objetos distintos disponíveis. Aqui, necessariamente, [tex]p\leq n.[/tex]
► [tex]~\boxed{CR\,_{n}^{p}=C_{n+p-1}^{p}= \dfrac{(p+n-1)!}{p! \cdot (n-1)!}}[/tex] é o número de maneiras de escolhermos [tex]p[/tex] objetos distintos ou não entre [tex]n[/tex] objetos distintos disponíveis. Aqui, a restrição de que [tex]\, p\leq n[/tex] não é necessária.
► Particularmente, o número [tex]CR\,_{n}^{p}[/tex] corresponde à quantidade de soluções inteiras não negativas de uma equação da forma [tex]x_{1}+x_{2}+\dots +x_{n}=p\,.[/tex]
Agora, vamos aos problemas!
Boa diversão!!!
Uma professora tem [tex]3[/tex] bolas de gude para distribuir para [tex]5[/tex] meninos (digamos, Alfredo, Bernardo, Carlos, Diogo e Eduardo).
De quantos modos ela pode fazer essa distribuição:
a) Supondo que ela dê as bolas para [tex]3[/tex] alunos distintos?
b) Supondo que os contemplados possam ganhar mais de uma bola?
[tex]\qquad C_{5}^{3}= \dfrac{5!}{3! \cdot (5-3)!}=10[/tex] modos.
b) Nesse item, chamemos de [tex]A[/tex], [tex]B[/tex], [tex]C[/tex], [tex]D[/tex] e [tex]E[/tex] a quantidade de bolas recebidas por Alfredo, Bernardo, Carlos, Diogo e Eduardo, respectivamente.
Para resolver esse problema, devemos ter [tex]A+B+C+D+E=3[/tex]. Como vimos anteriormente, o total de soluções inteiras não negativas dessa equação pode ser encontrada ao permutarmos [tex]7[/tex] elementos ([tex]3[/tex] bolas e [tex]4[/tex] traços).
Portanto, a professora pode distribuir as bolas de [tex]P_{7}^{3,4}= \dfrac{7!}{3! \cdot 4!}=\fcolorbox{black}{#E2C1A0}{$35$}\,[/tex] maneiras.
Se focarmos apenas na equação, concluímos que o número de soluções da equação [tex]\boxed{A+B+C+D+E=3}[/tex] é:
[tex]\qquad CR\,_{5}^{3}=C_{(5+3-1)}^{3}= \fcolorbox{black}{#E2C1A0}{$35$}\,.[/tex]
Num restaurante, são oferecidos [tex]4[/tex] tipos de carne, [tex]5[/tex] tipos de massa, [tex]8[/tex] tipos de salada e [tex]6[/tex] tipos de sobremesa.
De quantas maneiras diferentes podemos escolher uma refeição composta por [tex]2[/tex] carnes (distintas ou não), [tex]1[/tex] massa, [tex]2[/tex] saladas (distintas ou não) e [tex]1[/tex] sobremesa?
Decisão 1: escolher as duas carnes;
Decisão 2: escolher a massa;
Decisão 3: escolher as duas saladas;
Decisão 4: escolher a sobremesa.
- A quantidade de maneiras de tomarmos a primeira decisão pode ser calculada se utilizarmos a expressão definida para [tex]CR\,_{4}^{2}[/tex], que corresponde ao número de soluções inteiras não negativas da equação [tex]C_{1}+C_{2}+C_{3}+C_{4}=2[/tex], na qual [tex]C_{1}[/tex], [tex]C_{2}[/tex], [tex]C_{3}[/tex] e [tex]C_{4}[/tex] representam a quantidade de cada tipo de carne escolhida. Para saber o total de soluções dessa equação, precisamos conhecer o total de filas que conseguimos formar com [tex]2[/tex] bolas e [tex]3[/tex] traços, o que pode ser feito de [tex]P_{5}^{3,2}=\dfrac{5!}{3! \cdot 2!}=10[/tex] maneiras.
Assim, [tex]CR\,_{4}^{2}=C_{(4+2-1)}^{2}=10[/tex] soluções.
Portanto, há [tex]\boxed{10}[/tex] modos de escolher as duas carnes. - Como há [tex]5[/tex] tipos de massa e apenas uma será escolhida, temos [tex]\boxed{5}[/tex] maneiras de tomar essa decisão.
- Para escolher as duas saladas, devemos ter [tex]S_{1}+S_{2}+S_{3}+ \dots + S_{8}=2[/tex], sendo que [tex]S_{1}[/tex], [tex]S_{2}[/tex], [tex]S_{3}[/tex], [tex]\dots[/tex] e [tex]S_{8}[/tex] representam a quantidade de cada tipo de salada escolhida. Para saber o total de soluções dessa equação, precisamos conhecer o total de filas que conseguimos formar com [tex]2[/tex] bolas e [tex]7[/tex] traços, o que pode ser feito de [tex]P_{9}^{7,2}=\dfrac{9!}{7! \cdot 2!}=36[/tex] maneiras.
Como [tex]CR\,_{8}^{2}=C_{(8+2-1)}^{2}=36[/tex], então há [tex]\boxed{36}[/tex] modos de escolher as duas saladas. - Finalmente, como há [tex]6[/tex] tipos de sobremesa e apenas uma será escolhida, temos [tex]\boxed{6}[/tex] maneiras de tomar a última decisão.
Pelo Princípio Multiplicativo, temos [tex]\fcolorbox{black}{#E2C1A0}{$10 \cdot 5 \cdot 36 \cdot 6 =10800$}[/tex] modos de montar uma refeição.
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Quantas são as soluções inteiras não negativas da inequação [tex]x+y+z \leq 4[/tex]?
Observe, inicialmente, que a inequação [tex]x+y+z \leq 4[/tex] corresponde a cinco equações (não simultâneas):
I) [tex]x+y+z=0[/tex];
II) [tex]x+y+z=1[/tex];
III) [tex]x+y+z=2[/tex];
IV) [tex]x+y+z=3[/tex];
V) [tex]x+y+z=4[/tex].
Agora, é só calcular quantas soluções cada uma dessas equações possui e somar as respectivas quantidades.
Vamos lá!
- A primeira equação possui apenas uma solução; a saber [tex]x=0[/tex], [tex]y=0[/tex] e [tex]z=0.[/tex]
- A segunda equação possui três soluções:
“[tex]x=1[/tex], [tex]y=0[/tex] e [tex]z=0[/tex]”; “[tex]x=0[/tex], [tex]y=1[/tex] e [tex]z=0[/tex]” e “[tex]x=0[/tex], [tex]y=0[/tex] e [tex]z=1[/tex]”.
Para as demais vamos utilizar o esquema bola-traço.
- A terceira ([tex]x+y+z=2[/tex]) possui [tex]P_{4}^{2,2}=\dfrac{4!}{2! \cdot 2!}=6[/tex] soluções (total de filas com [tex]2[/tex] bolas e [tex]2[/tex] traços).
- A quarta ([tex]x+y+z=3[/tex]) possui [tex]P_{5}^{3,2}=\dfrac{5!}{3! \cdot 2!}=10[/tex] soluções (total de filas com [tex]3[/tex] bolas e [tex]2[/tex] traços).
- A quinta ([tex]x+y+z=4[/tex]) possui [tex]P_{6}^{4,2}=\dfrac{6!}{4! \cdot 2!}=15[/tex] soluções (total de filas com [tex]4[/tex] bolas e [tex]2[/tex] traços).
Portanto, são [tex]\fcolorbox{black}{#E2C1A0}{$1+3+6+10+15=35$}[/tex] soluções.
Solução 2:
O que aprendemos nessa Sala de Estudo foi resolver equações lineares cuja solução é formada por inteiros não negativos. Que tal fazer uma inequação “recair” em uma equação?
Dada a inequação [tex]x+y+z \leq 4[/tex], vamos chamar de [tex]f[/tex] a “folga” da solução, definida por [tex]f=4-(x+y+z)[/tex].
Assim:
- Se [tex]f=0[/tex], então [tex]x+y+z=4[/tex];
- Se [tex]f=1[/tex], então [tex]x+y+z=3[/tex];
- Se [tex]f=2[/tex], então [tex]x+y+z=2[/tex];
- Se [tex]f=3[/tex], então [tex]x+y+z=1[/tex];
- Se [tex]f=4[/tex], então [tex]x+y+z=0[/tex].
Portanto, para calcular a quantidade de soluções da inequação, basta calcular a quantidade de soluções da equação [tex]x+y+z+f=4[/tex], o que já sabemos ter [tex]\fcolorbox{black}{#E2C1A0}{$P_{7}^{4,3}=\dfrac{7!}{4! \cdot 3!}=35$}[/tex] soluções ([tex]4[/tex] bolas e [tex]3[/tex] traços).
Quantas são as soluções inteiras da equação [tex]A+B+C=10[/tex], sabendo que [tex]A \geq 1[/tex], [tex]B \geq 2[/tex] e [tex]C \geq 3[/tex]?
Para resolver esse problema, vamos fazer as seguintes mudanças de incógnitas:
[tex]\qquad \boxed{A=1+a}~[/tex] , [tex]~\boxed{B=2+b}~[/tex] e [tex]~\boxed{C=3+c}.[/tex]
Assim, segue que:
[tex]\qquad A+B+C=10\\
\qquad (1+a)+(2+b)+(3+c)=10\\
\qquad a+b+c+6=10\\
\qquad a+b+c=4.[/tex]
Dessa forma, a equação dada é equivalente à equação [tex]\boxed{a+b+c=4}\,[/tex] e as restrições [tex]~A \geq 1[/tex], [tex]~B \geq 2~[/tex] e [tex]~C \geq 3~[/tex] do enunciado transformam-se em [tex]~A-1 \geq 0[/tex], [tex]~B-2 \geq 0~[/tex] e [tex]~C-3\geq 0~[/tex], ou seja, [tex]~a \geq 0[/tex], [tex]~b \geq 0~[/tex] e [tex]~c\geq 0.[/tex]
Logo, como a equação [tex]a+b+c=4[/tex] possui [tex]P_{6}^{4,2}=15[/tex] soluções ([tex]4[/tex] bolas e [tex]2[/tex] traços), então a equação inicial, com todas as restrições, também possui [tex]\fcolorbox{black}{#E2C1A0}{$15$}[/tex] soluções.
Solução 2:
Poderíamos interpretar esse problema como:
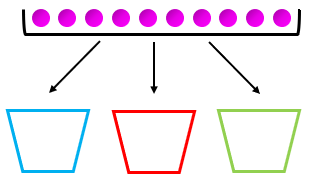
De quantas maneiras podemos distribuir dez bolas iguais em três caixas, de modo que:
- a primeira caixa tenha, pelo menos, uma bola;
- a segunda caixa tenha, pelo menos, duas bolas;
- a terceira caixa tenha, pelo menos, três bolas.
Assim, a princípio, a situação é essa: distribuir dez bolas em três caixas.
Mas, na prática, temos que distribuir apenas quatro bolas, pois uma das bolas já está na primeira caixa, duas já estão na segunda caixa e três, na terceira.
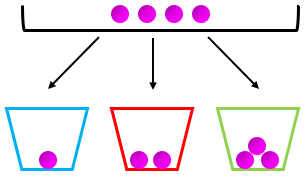
Assim, se [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] são as quantidades de bolas que distribuiremos na primeira caixa, na segunda caixa e na terceira, respectivamente, dentre as quatro restantes, a equação que de fato modela o problema é [tex]a+b+c=4\,.[/tex] E sabemos que essa equação possui [tex]15[/tex] soluções, já que:
[tex]\qquad CR_{3}^{4}=C_{6}^{4}=\dfrac{6!}{4! \cdot 2!}=\fcolorbox{black}{#E2C1A0}{$15$}\,.[/tex]
Quantos são os anagramas da palavra [tex]INSTITUTO[/tex] que não possuem duas letras [tex]T[/tex] juntas?
Observação: Anagrama é toda palavra formada com as mesmas letras de uma dada palavra, podendo ou não ter sentido na linguagem usual. Assim, os anagramas de uma dada palavra são as palavras obtidas pelo “embaralhamento” das letras da palavra original (manter as letras mudando ou não a ordem).
Vamos tomar duas decisões:
Decisão 1: Organizar as letras [tex]I, N, S, I, U[/tex] e [tex]O[/tex].
Observe que são [tex]6[/tex] letras, dentre as quais duas são repetidas. Assim, temos
[tex]\qquad P_{6}^{2}=\dfrac {6!}{2!}=360[/tex] maneiras.
Decisão 2: Após a organizar as letras [tex]I, N, S, I, U[/tex] e [tex]O[/tex], temos [tex]7[/tex] “espaços” para organizar as letras [tex]T[/tex].
Veja um exemplo na imagem a seguir.
![]()
Devemos, então, escolher três desses “espaços” para pôr as letras [tex]T[/tex], o que pode ser feito de
[tex]\qquad C_{7}^{3}=\dfrac {7!}{3! \cdot (7-3)!}=35[/tex] maneiras.
Finalizando, pelo Princípio Multiplicativo, temos [tex]\fcolorbox{black}{#E2C1A0}{$360 \cdot 35=12600$}[/tex] anagramas que não possuem duas letras [tex]T[/tex] juntas.
Solução 2:
Ao organizar as letras [tex]T[/tex], temos [tex]4[/tex] “espaços”:
Nesses “espaços” entrarão as letras [tex]I, N, S, I, U[/tex] e [tex]O[/tex].
Chamemos de [tex]A,B,C[/tex] e [tex]D[/tex] a quantidade de letras que ficarão nesses espaços.
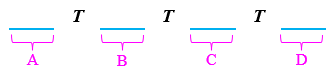
Assim, devemos ter [tex]A+B+C+D=6[/tex]; e, para que não haja duas letras [tex]T[/tex] juntas, devemos ter [tex]B\geq 1[/tex] e [tex]C \geq 1[/tex].
Fazendo [tex]B=b+1[/tex] e [tex]C=c+1[/tex], conseguimos descobrir o número de soluções da equação com as restrições, substituindo essas duas últimas igualdades na equação inicial:
[tex]\qquad A+B+C+D=6\\
\qquad A+b+1+c+1+D=6\\
\qquad A+b+c+D=4.[/tex]
A última equação possui [tex]P_{7}^{4,3}=35[/tex] soluções ([tex]4[/tex] bolas e [tex]3[/tex] traços).
Após escolhermos a quantidade de letras que entrarão em cada espaço, podemos ainda permutá-las, o que pode ser feito de [tex]P_{6}^{2}=\dfrac{6!}{2!}=360[/tex] maneiras.
Pelo Princípio Multiplicativo, temos [tex]\fcolorbox{black}{#E2C1A0}{$35 \cdot 360=12600$}[/tex] anagramas.
De quantas maneiras é possível colocar [tex]6[/tex] anéis diferentes em [tex]4[/tex] dedos da mão? (Considere apenas os casos em que haja pelo menos um anel em cada dedo.)
Pelo enunciado, fica claro que [tex]D_1+D_2+D_3+D_4=6[/tex] e que [tex]D_{1} \geq 1[/tex], [tex]D_{2} \geq 1[/tex], [tex]D_{3} \geq 1[/tex] e [tex]D_{4} \geq 1[/tex].
Fazendo [tex]\,\boxed{D_{1}=d_{1}+1}\;[/tex], [tex]\,\boxed{D_{2}=d_{2}+1}\;[/tex], [tex]\,\boxed{D_{3}=d_{3}+1}\;[/tex] e [tex]\,\boxed{D_{4}=d_{4}+1}\;[/tex] e substituindo essas igualdades na equação [tex]\boxed{D_1+D_2+D_3+D_4=6}[/tex], obtemos a equação [tex]d_{1}+d_{2}+d_{3}+d_{4}=2.[/tex]
Como a última equação possui [tex]P_{5}^{2,3}=\dfrac{5!}{2! \cdot 3!}=10[/tex] soluções, temos [tex]10[/tex] modos de decidir quantos anéis haverá em cada dedo. Porém, determinados em quais dedos vamos colocar anéis, devemos colocar os anéis neles, o que pode ser feito de [tex]P_{6}=6!=720[/tex] modos.
Portanto, pelo Princípio Multiplicativo, há [tex]\fcolorbox{black}{#E2C1A0}{$10\cdot 720=7200$}[/tex] modos de colocar [tex]6[/tex] anéis diferentes em [tex]4[/tex] dedos da mão.
Para o próximo problema, talvez você precise relembrar um pouquinho de probabilidade. Se quiser, visite esta página do nosso Blog!
Eugênio tem três dados que são dodecaedros regulares, com os números inteiros de [tex]1[/tex] a [tex]12[/tex] escritos nas faces.
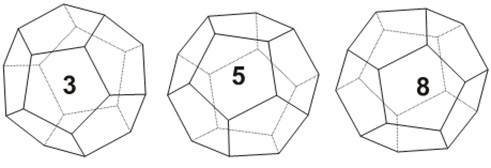
Eugênio sorteia um número inteiro jogando os três dados simultaneamente e somando os três números obtidos (ou seja, ele soma os três números que aparecem na face de cima de cada um dos dados).
a) Qual é a probabilidade de que o número sorteado seja igual a [tex]36[/tex]?
b) Qual é a probabilidade de que o número sorteado seja igual a [tex]30[/tex]?
c) Qual é a probabilidade de que o número sorteado seja maior ou igual a [tex]30[/tex]?
Para que possamos construir um espaço amostral equiprovável, devemos ter [tex]12 \cdot 12 \cdot 12=12^{3}=1728[/tex] casos possíveis. Desta forma, existe apenas um caso favorável [tex](12+12+12=36)[/tex].
Assim, a probabilidade em questão é [tex]\,\fcolorbox{black}{#E2C1A0}{$P=\dfrac{1}{1728}$}.[/tex]
b) Chamemos de [tex]X[/tex], [tex]Y[/tex] e [tex]Z[/tex] os números obtidos em um sorteio em cada dodecaedro.
Nesse item, devemos ter [tex]X+Y+Z=30[/tex], [tex]X \leq 12[/tex], [tex]Y \leq 12[/tex] e [tex]Z \leq 12[/tex].
Fazendo [tex]\boxed{X=12-x}[/tex], [tex]\boxed{Y=12-y}\,[/tex], [tex]\,\boxed{Z=12-z}[/tex] e substituindo essas expressões em [tex]X+Y+Z=30[/tex], obtemos a equação [tex]x+y+z=6[/tex].
Essa equação apresenta [tex]P_{8}^{6,2}=\dfrac{8!}{6! \cdot 2!}=28[/tex] soluções ([tex]6[/tex] bolas e [tex]2[/tex] traços), o que representa o número de casos favoráveis.
Portanto, a probabilidade neste item é dada por [tex]\,\fcolorbox{black}{#E2C1A0}{$P=\dfrac{28}{1728}=\dfrac{7}{432}$}.[/tex]
c) Chamemos. mais uma vez, de [tex]X[/tex], [tex]Y[/tex] e [tex]Z[/tex] os números obtidos em cada dodecaedro. Aqui, devemos ter:
[tex]\qquad 30\leq X+Y+Z \leq36\,[/tex] ; [tex]\,X \leq 12[/tex] ; [tex]\,Y \leq 12\,[/tex] ; [tex]\,Z \leq 12[/tex].
Para resolver essa inequação simultânea, vamos chamar de [tex]F[/tex] a “folga” da solução, definida por [tex]F=36-(X+Y+Z)[/tex]. Note que [tex]F \leq 6[/tex].
Fazendo [tex]\boxed{X=12-x},\; \boxed{Y=12-y}, \,\boxed{Z=12-z}[/tex], teremos a seguinte “folga”:
[tex]\qquad F=36-(12-x)-(12-y)-(12-z)=x+y+z \leq 6[/tex].
Assim, fazendo [tex]F=6-f[/tex], obtemos finalmente [tex]x+y+z+f=6[/tex]
A última equação apresenta [tex]P_{9}^{6,3}=\dfrac{9!}{6! \cdot 3!}=84[/tex] soluções ([tex]6[/tex] bolas e [tex]3[/tex] traços), o que corresponde ao número de casos favoráveis.
Portanto, a probabilidade é [tex]\,\fcolorbox{black}{#E2C1A0}{$P=\dfrac{84}{1728}=\dfrac{7}{144}$}.[/tex]
Agora é com vocês….
Que tal fazer alguns exercícios?
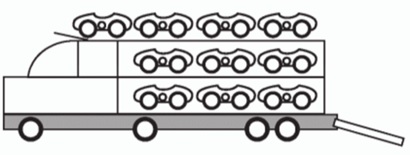
No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores: amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha tem uma cor fixa. A empresa determinou que em todo caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo. Com base nessas informações, quantos são os modelos distintos do brinquedo caminhão-cegonha que essa empresa poderá produzir?
a) [tex]C_{6,4}[/tex]
b) [tex]C_{9,3}[/tex]
c) [tex]C_{10,4}[/tex]
d) [tex]6^{4}[/tex]
e) [tex]4^{6}[/tex]

a) [tex]91[/tex]
b) [tex]136[/tex]
c) [tex]150[/tex]
d) [tex]200[/tex]
e) [tex]210[/tex]
a) [tex]1287[/tex]
b) [tex]14112[/tex]
c) [tex]44200[/tex]
d) [tex]58212[/tex]
e) [tex]62822[/tex]
- Para saber o número total de maneiras de desembarcar as mulheres, basta calcular o número total de soluções da equação [tex]E_{1}+E_{2}+E_{3}+E_{4}+E_{5}+E_{6}=6[/tex].
- Analogamente, o desembarque dos homens pode ser calculado por [tex]E_{1}+E_{2}+E_{3}+E_{4}+E_{5}+E_{6}=4[/tex].
A primeira equação possui [tex]P_{11}^{6,5}[/tex] soluções e a segunda, [tex]P_{9}^{4,5}[/tex].
Utilizando o Princípio Multiplicativo temos como resposta:
[tex]\qquad P_{11}^{6,5} \cdot P_{9}^{4,5}=462 \cdot 126=58212[/tex].
(Obs: Não foi necessário permutar os passageiros, pois no enunciado foi dito que não há distinção entre passageiros do mesmo sexo.)
Note que o tenista deverá descansar em exatamente um dia por bloco.
Se alguma vez ele descansa no dia central de um bloco depois disso ele não poderá descansar no último dia de um bloco; analogamente, se alguma vez ele descansa no primeiro dia de um bloco ele deverá descansar no primeiro dia de todos os blocos que vierem depois.
Assim, ele deve descansar no último dia nos primeiros [tex]z[/tex] blocos, depois descansar no dia central durante [tex]y[/tex] blocos e finalmente descansar no primeiro dia nos últimos [tex]x[/tex] blocos, onde [tex]x + y + z = 10[/tex].
Já vimos que para encontrar o total de soluções inteiras não negativas dessa equação basta contar o número de filas que podemos formar com [tex]12[/tex] elementos ([tex]10[/tex] bolas e [tex]2[/tex] traços).
Assim, o tenista possui [tex]P_{12}^{10,2}=\dfrac{12!}{10! \cdot 2!}=66[/tex] maneiras de descansar nesses dias.
Equipe COM – OBMEP
[1] A Matemática do Ensino Médio (volume 2): Coleção do Professor de Matemática – Elon Lages Lima; Paulo Cesar Pinto Carvalho; Eduardo Wagner e Augusto César Morgado.
[2] A Matemática do Ensino Médio (volume 4): Coleção do Professor de Matemática – Elon Lages Lima; Paulo Cesar Pinto Carvalho; Eduardo Wagner e Augusto César Morgado.
[3] Matemática Discreta: Coleção Profmat – Augusto César Morgado; Paulo Cesar Pinto Carvalho.
[4] Análise Combinatória e Probabilidade – Augusto César Morgado; João Bosco Pitombeira de Carvalho; Paulo Cesar Pinto Carvalho e Pedro Fernandez.
[5] Círculo Matemático de Moscou: Problemas semana-a-semana – Sergey Dorichenko.
[6] Círculos Matemáticos: A Experiência Russa – Dimitri Fomin; Sergey Genkin e Ilia Itenberg.
[7] Notas de aulas do professor Cleber Gouvêa Fernandes (IFRJ).
