Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 6º ano do E. F. – Nível de dificuldade: Médio)
Dois dados comuns foram encostados em uma parede, de modo que só é possível ver três faces de cada um. Marquinhos se aproximou dos dois dados e contou 27 pontos desenhados nessas faces.
Qual o total de pontos que Marquinhos pode ter visto em cada um dos dois dados?

Dica
Em um dado comum, a soma dos pontos de duas faces opostas é sempre [tex]7[/tex].
Se necessário, você pode utilizar o applet abaixo para visualizar essa afirmação.
Um applet para ajudar
Instruções:
(1) Espere o applet carregar. (O aplicativo abrirá uma janela 3D; assim, ele pode demorar um pouquinho para carregar.)
(2) Para movimentar o dado, clique em qualquer lugar da janela do aplicativo com o botão esquerdo do mouse, mantenha o mouse pressionado e faça o movimento.
OBMEP_ srdg, criado com o GeoGebra
Solução
A maior soma de pontos possíveis em três faces de um dado é [tex]6+5+4=15[/tex]. Dessa forma, a quantidade de pontos que Marquinhos viu em cada dado define duas somas, cada uma valendo no máximo [tex]15[/tex], cuja soma é [tex]27[/tex]. (É uma soma de somas, mesmo!).
Observe que:
- Se uma das somas for [tex]15[/tex], a outra será [tex]12[/tex].
- Se uma das somas for [tex]14[/tex], a outra será [tex]13[/tex].
- Se uma das somas for [tex]13[/tex], a outra será [tex]14[/tex].
- Se uma das somas for [tex]12[/tex], a outra será [tex]15[/tex].
- Se uma das somas for [tex]11[/tex], ou menos do que [tex]11[/tex], mesmo que a outra seja [tex]15[/tex], que é o máximo possível, a soma das duas somas seria menor do que [tex]27[/tex]: [tex]11+15=26\lt27[/tex], [tex]10+15=25\lt27[/tex], e assim por diante.
Portanto, temos apenas duas possibilidades: [tex]\boxed{\text{15 e 12}}[/tex] ; [tex]\boxed{\text{14 e 13}}.[/tex]
Será que na prática ambas são possíveis, já que pela posição dos dois dados não é possível observar duas faces que sejam opostas? Vejamos…
- As somas [tex]\boxed{\text{15 e 12}}[/tex] são possíveis de serem obtidas; veja o esqueminha abaixo.
- No caso das somas [tex]\boxed{\text{14 e 13}}[/tex], temos um problema com a soma [tex]13[/tex].
- Utilizando o [tex]6[/tex] teríamos os seguintes casos:
- Utilizando o [tex]5[/tex] teríamos os seguintes casos:
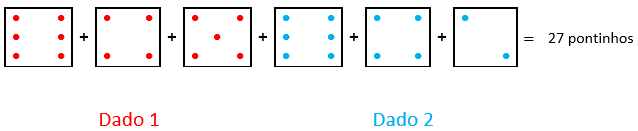
Observe também que, em cada dado, as faces que contêm a quantidade necessária de pontinhos são adjacentes e, portanto, não temos duas faces opostas sendo utilizadas.
Observe que se utilizarmos números naturais distintos menores do que [tex]5[/tex], a maior soma possível seria [tex]4+3+2=9[/tex] e não [tex]13[/tex]. Logo, devemos utilizar o [tex]5[/tex] ou o [tex]6[/tex] na soma de [tex]13[/tex]. Vejamos as possibilidades.
[tex]\qquad \boxed{6+6+1=13}[/tex]; mas não temos duas faces distintas com seis pontinhos.
[tex]\qquad \boxed{6+5+2=13}[/tex]; mas [tex]2[/tex] e [tex]5[/tex] são faces opostas.
[tex]\qquad \boxed{6+4+3=13}[/tex]; mas [tex]3[/tex] e [tex]4[/tex] são faces opostas.
[tex]\qquad \boxed{6+3+4=13}[/tex]; possibilidade já analisada.
[tex]\qquad \boxed{6+2+5=13}[/tex]; possibilidade já analisada.
[tex]\qquad \boxed{6+1+6=13}[/tex]; possibilidade já analisada.
[tex]\qquad \boxed{5+6+2=13}[/tex]; mas [tex]2[/tex] e [tex]5[/tex] são faces opostas.
[tex]\qquad \boxed{5+5+3=13}[/tex]; mas não temos duas faces distintas com cinco pontinhos.
[tex]\qquad \boxed{5+4+4=13}[/tex]; mas não temos duas faces distintas com quatro pontinhos.
[tex]\qquad \boxed{5+3+5=13}[/tex]; possibilidade já analisada.
[tex]\qquad \boxed{5+2+6=13}[/tex]; possibilidade já analisada.
[tex]\qquad \boxed{5+1+7=13}[/tex]; mas não temos faces com sete pontinhos.
Então, de fato, não conseguimos obter [tex]13[/tex] a partir de três faces adjacentes de um dado comum.
Portanto, Marquinhos viu um total de [tex] \, \fcolorbox{black}{#eee0e5}{$ 15\,$}[/tex] em um dado e [tex] \, \fcolorbox{black}{#eee0e5}{$ 12\,$}[/tex] no outro.
Você pode visualizar a solução [tex]15+12[/tex] usando o applet disponibilizado a seguir.
Outro applet para ajudar
Instruções:
(1) Espere o applet carregar. (O aplicativo abrirá uma janela 3D; assim, ele pode demorar um pouquinho para carregar.)
(2) Para ter a mesma visualização do Marquinhos, clique em qualquer lugar da janela do aplicativo com o botão esquerdo do mouse, mantenha o mouse pressionado e o movimente.
OBMEP_ srdg, criado com o GeoGebra
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
