Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
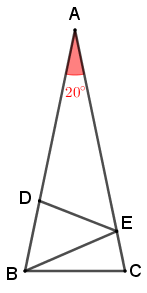
(OPM, 2014 – Adaptado) Na figura abaixo vemos um triângulo isósceles [tex]ABC[/tex] de base [tex]\overline{BC}[/tex] medindo [tex]10\, cm[/tex] e cuja medida do ângulo relativo ao vértice [tex]\hat{A}[/tex] é [tex]20^\circ.[/tex]
Sobre os segmentos [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] foram marcados os pontos [tex]D[/tex] e [tex]E[/tex], ficando então definidos os segmentos [tex]\overline{ED}[/tex] e [tex]\overline{EB}[/tex], ambos com comprimento [tex]10\, cm.[/tex]
Qual é a medida do segmento [tex]\mathbf{\overline{BD}}\, [/tex]?

Lembretes
(1) A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex].
(2) Todo triângulo isósceles possui os ângulos da base com a mesma medida.
Notações:
– Denotaremos a medida do ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]X\widehat{V}Y. [/tex]
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
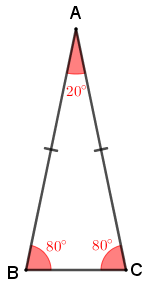
O triângulo [tex]ABC[/tex] é isósceles com base [tex]\overline{BC}[/tex]; assim, seus ângulos internos com vértices em [tex]B[/tex] e [tex]C[/tex] têm a mesma medida. Com isso, como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex], segue que:
- [tex] A \widehat{B} C=A\widehat{C}B=\dfrac{180^\circ-20^\circ}{2}=80^\circ.[/tex]
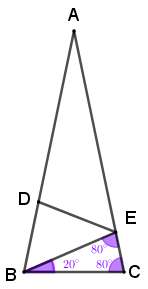
Perceba agora que o triângulo [tex]EBC[/tex] é isósceles com base [tex]\overline{EC}[/tex], já que [tex]\overline{EB}[/tex] e [tex]\overline{BC}[/tex] têm o mesmo comprimento. Logo, segue que:
- [tex] E \widehat{B} C=180^\circ-80^\circ-80^\circ=20^\circ.[/tex]
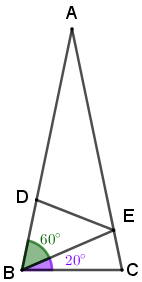
Como [tex] A \widehat{B} C=80^\circ[/tex], [tex] E \widehat{B} C=20^\circ[/tex] e [tex] A \widehat{B} C= E \widehat{B} C+D \widehat{B}E[/tex], concluímos que:
- [tex]D \widehat{B}E= A \widehat{B} C-E \widehat{B} C=80^\circ-20^\circ=60^\circ[/tex].
 |
 |
 |
Você pode estar se perguntando o que todas essas medidas de ângulos têm a ver com um problema no qual precisamos encontrar uma medida de segmento, não é?
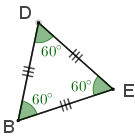
Mas observe que os segmentos [tex]\overline{ED}[/tex] e [tex]\overline{EB}[/tex] têm o mesmo comprimento e, portanto, o triângulo [tex]EDB[/tex] é isósceles. Dessa forma, [tex]B\widehat{D}E= D\widehat{B}E=60^\circ[/tex] e, daí resulta que:
- [tex] D \widehat{E} B=180^\circ-B\widehat{D}E-D\widehat{B}E=180^\circ-60^\circ-60^\circ=60^\circ.[/tex]
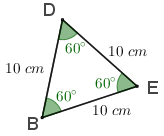
Com isso, podemos concluir que o triângulo [tex]EDB[/tex] é mais do que um triângulo isósceles: [tex]EDB[/tex] é um triângulo equilátero!
E como [tex]\overline{ED}[/tex] e [tex]\overline{EB}[/tex] têm comprimento [tex]10\, cm[/tex], todas as medidas angulares que encontramos nos permitem, finalmente, concluir que a medida do segmento [tex]\overline{BD}[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$10\,cm$}.[/tex]
 |
 |
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
