Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Difícil)
Determine a quantidade de números naturais [tex] \, \boxed{ n=abcd} \, [/tex], de quatro dígitos distintos e não nulos, tais que
[tex]\quad \bullet \, a \gt b[/tex],
[tex]\quad \bullet \, c \gt b[/tex],
[tex]\quad \bullet \, c \gt d.[/tex]

Uma ajuda para os mais novos
Para uma visualização da solução que apresentaremos, utilizaremos uma representação geométrica para os algarismos [tex] \, a, \, b \, , \, c \, , \, d \, .[/tex]
Esse tipo de representação é comum para quem já estudou geometria analítica, mas quem ainda não estudou esse assunto não terá dificuldade de entender o que faremos.
- Vamos representar dois ou mais números naturais distintos como pontos de um segmento de reta, de modo que um número maior seja sempre colocado à direita de um menor.
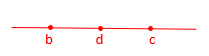
Por exemplo, se [tex]x \, , \, y \, , \, z \, [/tex] são números naturais tais que [tex]y \lt z \lt x [/tex], podemos representá-los como indicado abaixo.
Solução
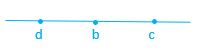
Observe que, pelos dados do problema, [tex] \, b \lt c \, [/tex] e [tex] \, d \lt c.[/tex] Assim, olhando os números [tex] \, \, b \, , \, c \, , \, d \, [/tex] como pontos de um segmento, [tex]c[/tex] está à direita de [tex]b[/tex] e à direita de [tex]d[/tex].
![]()
No entanto, não temos informações comparativas entre [tex]b \, [/tex] e [tex] \, d[/tex]; assim, temos que considerar as duas situações possíveis:
|
► [tex] \, b \lt d\lt c [/tex]
|
► [tex] \, d \lt b\lt c \, [/tex] |
Mas, e o algarismo [tex]a[/tex]?
A única informação que temos sobre [tex]a[/tex] é a de que [tex]a \gt b[/tex]; dessa forma, vamos inserir essa informação nas duas situações acima descritas. Acompanhe…
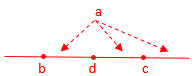
► Do primeiro caso, [tex] \, b \lt d\lt c \, [/tex], resulta que:
|
 |
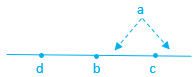
► Do segundo caso, [tex] \, d \lt b\lt c \, [/tex], resulta que:
|
 |
Temos, então cinco possibilidades para os algarismos que satisfazem as condições do problema. Embora cada uma dessas possibilidades gere números [tex]n=abcd [/tex] distintos, podemos contá-las da mesma maneira. Assim, só precisamos contar de quantas maneiras podemos escolher quatro dentre os números [tex]1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9 [/tex]; cada maneira gera cinco números [tex]n[/tex], cada um satisfazendo uma das cinco condições. Por exemplo, se temos os algarismos [tex]2, \, 8, \, 1, \, 5 [/tex], então:
- fazemos [tex] \, b=1, \, a=2, \, d=5, \, c=8[/tex] e obtemos [tex] \, \boxed{ n=2185} \, [/tex];
- fazemos [tex] \, b= 1, \, d=2, \, a=5, \, c=8[/tex] e obtemos [tex] \, \boxed{ n=5182} \, [/tex];
- fazemos [tex] \, b =1, \, d=2, \, c =5, \, a=8[/tex] e obtemos [tex] \, \boxed{ n=8152} \, [/tex];
- fazemos [tex] \, d =1, \, b =2, \, a=5, \, c=8 \, [/tex] e obtemos [tex] \, \boxed{ n=5281} \, [/tex];
- fazemos [tex] \, d=1, \, b=2, \, c =5, \, a=8[/tex] e obtemos [tex] \, \boxed{ n=8251} \, [/tex].
► Os quatro números devem ser escolhidos dentre os nove possíveis sem nos preocuparmos com a ordem, já que, depois de escolhidos, eles serão ordenados convenientemente de cinco formas diferentes. A escolha de quatro entre os nove números poderá ser feita de [tex]C_{9,4}[/tex] modos distintos, onde [tex]C_{9,4}[/tex] indica uma combinação dos [tex]9[/tex] elementos tomados [tex]4[/tex] a [tex]4[/tex]:
[tex]\qquad C_{9,4}=\binom{9}{4}=\dfrac{9!}{(9-4)! \, 4!}=\dfrac{9!}{5! \, 4!}=126[/tex] modos.
► Cada uma das [tex]126[/tex] escolhas gera cinco números que atendem as exigências do problema; assim, o total de números que atendem as condições do problema é [tex] \, \fcolorbox{black}{#eee0e5}{$126 \times 5=630$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |