(A) Problema para ajudar na escola: Quadrado Mágico

Problema
(A partir do 7º ano do E. F. – Nível de dificuldade: Difícil)

---

Um Quadrado Mágico (QM) de ordem $3$ é construído distribuindo-se os números de $1$ a $9$ nas casas de uma tabela $3 \times 3$, um em cada casa, de maneira que a soma dos números de cada coluna, linha ou diagonal seja sempre a mesma.

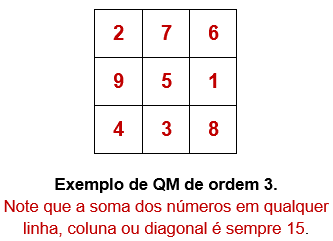
Explique porque, na construção de um QM de ordem $3$, o número $5$ deve ser colocado necessariamente no centro da tabela.

Solução

---

Em primeiro lugar, note que $1+2+…+9=45$ e, como os números são distribuídos em três linhas de mesma soma, esta soma constante (chamada Constante Mágica) deve ser $45\div3=15 .$
Uma das explicações mais elegantes sobre o motivo pelo qual o $5$ deve ser colocado necessariamente no centro do quadrado tem a ver com as possíveis somas de três números de $1$ a $9$, com resultado $15$, sem repetição de números.
São elas:
$\qquad 1+5+9=15$
$\qquad 1+6+8=15$
$\qquad 2+4+9=15$
$\qquad 2+5+8=15$
$\qquad 2+6+7=15$
$\qquad 3+4+8=15$
$\qquad 3+5+7=15$
$\qquad 4+5+6=15$ .
Note, agora, que o número do centro do QM deve ser uma das parcelas de quatro somas distintas com resultado $15$ (somas de uma linha, de uma coluna e de duas diagonais).

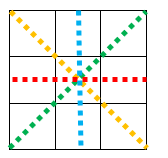
Mas, verificando as opções acima, observamos que o único número que faz parte de quatro somas distintas é o $5$:
$\qquad 1+\fcolorbox{black}{#eee0e5}{$5$}+9=15$
$\qquad 2+\fcolorbox{black}{#eee0e5}{$5$}+8=15$
$\qquad 3+\fcolorbox{black}{#eee0e5}{$5$}+7=15$
$\qquad 4+\fcolorbox{black}{#eee0e5}{$5$}+6=15$.
Assim, o número $5$ deve ser colocado, necessariamente, no centro da tabela que define um Quadrado Mágico (QM) de ordem $3$.

---

Solução elaborada pelos Moderadores do Blog.