Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio )
(UFSCAR, 2007 – Adaptado) Você já deve ter visto parafusos do tipo sextavado. Esse tipo de parafuso é assim denominado pois sua cabeça, local onde se encaixa a chave para apertá-lo ou desapertá-lo, tem seis lados.
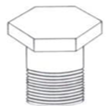
Considere que a chave visualizada à direita da figura abaixo se encaixe perfeitamente na cabeça do parafuso sextavado mostrado à esquerda da figura.
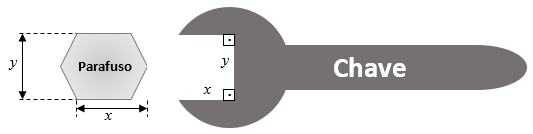
Se a cabeça do parafuso é um hexágono regular cujos lados medem [tex]3\, [/tex]cm , calcule as medidas [tex]x[/tex] e [tex]y[/tex] indicadas na figura.

Lembretes
✐ A partir do seu centro, um hexágono regular pode ser decomposto em seis triângulos equiláteros congruentes cujo comprimento dos lados é o comprimento dos lados do próprio hexágono.
OBMEP_srg, criado com o GeoGebra
✐ Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
De acordo com o Lembrete, vamos decompor o hexágono regular [tex]ABCDEF[/tex] que define a cabeça do parafuso em seis triângulos equiláteros congruentes cujos lados medem [tex]3\, [/tex]cm, a partir do centro [tex]O.[/tex] Em particular, vamos dar destaque aos triângulos equiláteros [tex]\textcolor{#CC66FF}{CDO}[/tex] e [tex]\textcolor{#009900}{BCO}.[/tex]
Como esses triângulos são equiláteros, as respectivas alturas [tex]\overline{DM}[/tex] e [tex]\overline{BM}[/tex] relativas ao lado comum [tex]\overline{OC}[/tex] são também medianas; logo, os segmentos [tex]\overline{OM}[/tex] e [tex]\overline{MC}[/tex] medem [tex]1,5\, [/tex]cm cada um.
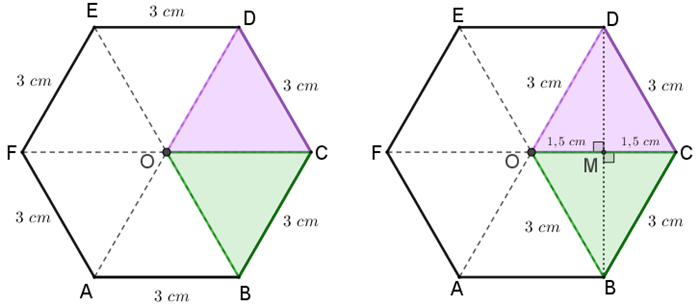
Dessa forma, observando a figura abaixo podemos concluir que:
[tex]\qquad x=AH\\
\qquad x=AB+BH\\
\qquad x=3\text{ cm}+1,5\text{ cm}\\
\qquad \, \fcolorbox{black}{#eee0e5}{$x=4,5 \text{ cm}$}\, .[/tex]
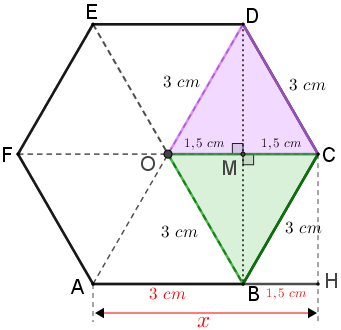
Para obtermos a medida [tex]y[/tex] será necessário determinarmos antes a medida das alturas [tex]\overline{DM}[/tex] e [tex]\overline{BM}[/tex]. Para isso, basta aplicarmos o Teorema de Pitágoras em um dos triângulos [tex]\textcolor{#CC66FF}{CDO}[/tex] ou [tex]\textcolor{#009900}{BCO}:[/tex]
[tex]\qquad h^2+(1,5)^2=3^2\\
\qquad h^2=9-2,25\\
\qquad h^2=6,75\\
\qquad h=\pm\sqrt{6,75}.[/tex]
Como [tex]h\gt 0[/tex], segue que [tex] h=\sqrt{6,75}\text{ cm}\\[/tex].
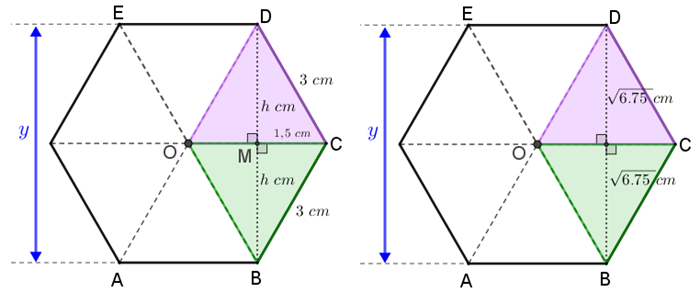
Observando as figuras acima, podemos concluir que:
[tex]\qquad y=DB\\
\qquad y=DM+MB\\
\qquad \, \fcolorbox{black}{#eee0e5}{$y=2\, \sqrt{6,75}\text{ cm}$}\, .[/tex]
Se você prefere trabalhar com frações, observe que:
[tex]\qquad h^2+\left(\dfrac{3}{2}\right)^2=3^2\\
\qquad h^2=9-\dfrac{9}{4}\\
\qquad h^2=\dfrac{27}{4}\\
\qquad h=\sqrt{\dfrac{27}{4}}=\dfrac{3\sqrt{3}}{2}\, ,[/tex]
donde
[tex]\qquad y=DB=2h\\
\qquad y=2\times\dfrac{3\sqrt{3}}{2}\\
\qquad \, \fcolorbox{black}{#eee0e5}{$y=3\sqrt{3}\text{ cm}$}\, .[/tex]
De qualquer modo, [tex]y[/tex] é aproximadamente [tex]5,2\text{ cm}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
