✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
Determinar a área de um trapézio [tex]ABCD[/tex], com bases [tex]\overline{AB}[/tex] e [tex]\overline{CD}[/tex], sabendo-se que [tex]AB = 52 \text{ cm}[/tex], [tex]BC = 12 \text{ cm}[/tex], [tex]CD = 39\text{ cm}[/tex], [tex]DA = 5 \text{ cm}[/tex].
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
Ajuda
Um dos resultados mais conhecidos da Geometria é o "Teorema de Pitágoras":
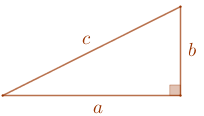
Se um triângulo retângulo tem catetos com comprimentos [tex]a \, [/tex] e [tex] \, b[/tex] e hipotenusa com comprimento [tex]c[/tex], então [tex]\boxed{a^2+b^2=c^2} \, .[/tex]
Mas o que muitas pessoas não sabem é que a recíproca desse teorema também é verdadeira:
Se os lados de um triângulo medem [tex]a \, [/tex], [tex] \, b \, [/tex] e [tex] \, c \, [/tex] e [tex]\boxed{a^2+b^2=c^2} \, [/tex], então esse é um triângulo retângulo cuja hipotenusa tem comprimento [tex]c \, .[/tex]
Solução
Pelo vértice [tex]D[/tex] do trapézio, trace uma paralela ao lado [tex]\overline{BC}[/tex], obtendo o ponto [tex]P[/tex] sobre [tex]\overline{AB}[/tex]. Assim, [tex]PBCD[/tex] é um paralelogramo.
Como os lados paralelos de um paralelogramo têm as mesmas medidas, então:
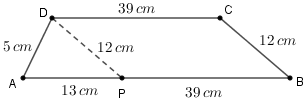
- [tex] PB = 39 \text{ cm}\, [/tex] e [tex] \, DP=12 \text{ cm}.[/tex]
Observe, na figura de referência ao lado, que ficou definido um triângulo [tex] APD[/tex] cujos lados medem
- [tex]AP = 52-39 = 13 \text{ cm}[/tex], [tex] PD = 12 \text{ cm}\, [/tex] e [tex] \, AD = 5 \text{ cm}.[/tex]
Por outro lado, temos que [tex]5^2+12^2=169=13^2[/tex]; assim, de acordo com a Ajuda, [tex] APD[/tex] é um triângulo retângulo e o ângulo [tex]\angle ADP[/tex] é reto, conforme mostra a nova figura de referência abaixo.
Como precisaremos da altura [tex]\textcolor{red}{h}[/tex] do trapézio para calcularmos a sua área, vamos utilizar o triângulo [tex] APD[/tex] para obtê-la.
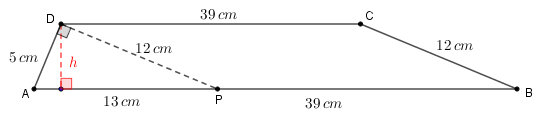
Perceba que cada cateto de um triângulo retângulo pode ser tomado como a altura relativa ao outro cateto; assim, a área [tex]S[/tex] de [tex] APD[/tex] pode ser assim calculada:
[tex]\quad S=\dfrac{\text{base}\times\text{altura}}{2}=\dfrac{5\times 12}{2}=30 \, .[/tex]
Mas, [tex]\textcolor{red}{h}[/tex] é a medida da altura de [tex] APD[/tex] relativa à hipotenusa [tex] \overline{AP}[/tex]; assim, a área [tex]S[/tex] também é dada por [tex]S=\dfrac{13 \times \textcolor{red}{h}}{2}[/tex] e, como [tex]S=30 \, [/tex], então:
[tex]\qquad S=\dfrac{13 \times h}{2}[/tex]
[tex]\qquad 30=\dfrac{13 \times h}{2}[/tex]
[tex]\qquad 60=13 \times h[/tex]
[tex]\qquad h=\dfrac{60}{13} \, .[/tex]
Pronto, já podemos calcular a área do trapézio [tex]ABCD[/tex]:
[tex]\qquad \begin{align*}Área_{trapézio}&=\dfrac{\left(\text{base maior+base menor}\right)\times\text{altura}}{2}\\
&=\dfrac{\left(52+39\right) \times \frac{60}{13}}{2}\\
&=\dfrac{\left(91\right) \times \frac{60}{13}}{2}\\
&=\dfrac{\cancel{91}\times 60}{2\times \cancel{13}}\\
&=\dfrac{7\times \cancel{60}}{\cancel{2}}\\
&=\boxed{210} \, .
\end{align*}[/tex]
Portanto, a área do trapézio [tex]ABCD[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$210 \text{ cm}^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Difícil
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
