✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Médio)
(OPM 2008 – adaptado) O desenho abaixo foi feito em um papel quadriculado.
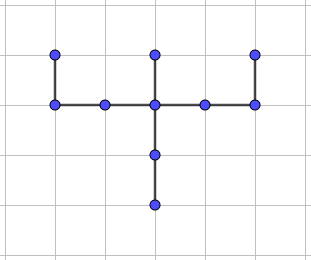Quantos triângulos com vértices nos pontos da figura desenhada é possível construir?
Ajuda
O número de combinações de [tex]n[/tex] elementos, tomados [tex]p[/tex] a [tex]p [/tex], é definido como o "número de maneiras possíveis de escolhermos [tex]p[/tex] objetos a partir de [tex]n[/tex] objetos disponíveis, sem que a ordem utilizada na escolha seja levada em consideração".
Esse número é representado pelos símbolos [tex]C_n^p[/tex] ou [tex]C_{n,p}[/tex] e é dado por:
[tex] \boxed{C_n^p=\dfrac{n!}{\left(n-p\right)! \, p!}}[/tex] .
Solução
Sabemos que para definir um triângulo precisamos de três pontos não colineares; mas vamos inicialmente calcular o número de escolhas possíveis de três pontos quaisquer dentre os dez pontos apresentados, sem que a ordem de escolha seja levada em consideração:
[tex]\qquad C_{10}^3=\dfrac{10!}{\left(10-3\right)! \, 3!}=\dfrac{\cancel{10!}}{\cancel{7!} \, 3!}=\dfrac{10\times 9\times 8}{3\times 2}=\boxed{120}[/tex] .
Mas nestas [tex]120[/tex] escolhas estão incluídas aquelas nas quais os três pontos são colineares, que sabemos não definirem um triângulo. Vamos então descontar desse total a quantidade de escolhas com três pontos colineares. Para isso, veja que temos três tipos de escolha de pontos colineares:
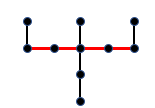
- Os pontos que estão sobre o segmento vermelho indicado na figura ao lado
Neste caso temos
[tex]\qquad C_5^3=\dfrac{5!}{\left(5-3\right)! \, 3!}=\dfrac{\cancel{5!}}{2!\cancel{3!}}=\dfrac{5\times 4}{2}=\boxed{10}[/tex] escolhas.
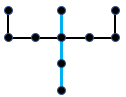
- Os pontos que estão sobre o segmento azul indicado na segunda figura ao lado
Neste caso temos
[tex]\qquad C_4^3=\dfrac{4!}{\left(4-3\right)! \, 3!}=\dfrac{\cancel{4!}}{1!\cancel{3!}}=\boxed{4}[/tex] escolhas.
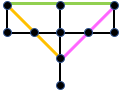
- As escolhas coloridas indicadas na terceira figura ao lado
Neste caso temos [tex]\boxed{3}[/tex] escolhas.
Assim, contamos a mais [tex]\boxed{10+4+3=17}[/tex] escolhas, quando calculamos as [tex]120[/tex] iniciais e, portanto,
o número de triângulos que se pode construir com vértices nos pontos da figura é igual a [tex]\fcolorbox{black}{#eee0e5}{$120 − 17 = 103$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |