Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Uma fábrica produz vários modelos para bandeirinhas que podem ser utilizadas em festas de aniversário.
Bianca escolheu, para a sua festa de dez anos, bandeirinhas confeccionadas em quadrados de papel nos quais são desenhados dois quadrados coloridos de verde e de azul e cujos vértices são pontos médios dos lados dos quadrados nos quais estão inscritos, conforme mostra a figura.
Em cada bandeirinha, qual a fração que está colorida de azul?

Solução
Para resolver este problema, vamos precisar da relação entre a área de um quadrado e a área do quadrado definido pelos pontos médios do primeiro quadrado.
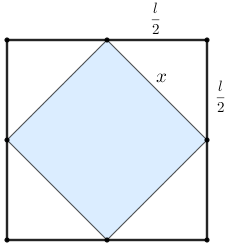
- Se você conhece o Teorema de Pitágoras, chame de [tex]l[/tex] o comprimento dos lados do quadrado inicial.
Ligando os pontos médios de dois lados adjacentes desse quadrado, obtemos um triângulo retângulo cujos catetos medem ambos [tex]\dfrac{l}{2}[/tex] e cuja hipotenusa é o lado do quadrado menor, de medida, digamos, [tex]x[/tex].
Então, pelo Teorema de Pitágoras:
[tex]\qquad\qquad x^2=\left(\dfrac{l}{2}\right)^2+\left(\dfrac{l}{2}\right)^2[/tex]
[tex]\qquad\qquad x^2=\dfrac{l^2}{4}+\dfrac{l^2}{4}=\dfrac{l^2}{2}.[/tex]
Sendo [tex]x \, [/tex] e [tex] \, l[/tex] medidas de lados de quadrados, [tex]x\gt 0 \, [/tex] e [tex] \, l\gt 0[/tex]; logo,
[tex]\qquad x=\sqrt{\dfrac{l^2}{2}}=\dfrac{l}{\sqrt{2}}.[/tex]
Agora, observe que a área do quadrado interno é [tex] x^2=\boxed{\dfrac{l^2}{2}} \, [/tex] e a área do quadrado inicial é [tex]\boxed{l^2} \, [/tex]; assim, a área do quadrado interno é metade da área do quadrado inicial.
- Agora, se você não conhece o Teorema de Pitágoras, chame de [tex]l[/tex] o comprimento dos lados do quadrado inicial e de [tex]x[/tex] o comprimento dos lados do quadrado menor.
Trace o segmento horizontal e o segmento vertical determinados pelos pontos médios do quadrado maior (vértices do quadrado menor) e observe que ficam definidos oito triângulos retângulos cujos catetos medem ambos [tex]\dfrac{l}{2}[/tex] e cuja hipotenusa mede [tex]x[/tex].
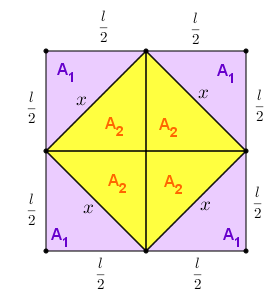
Esses oito triângulos são congruentes e cada um tem área [tex]\dfrac{\frac{l}{2}\times \frac{l}{2}}{2}=\dfrac{l^2}{8} \, [/tex]; assim, [tex]\boxed{A_1=\dfrac{l^2}{8}} \, [/tex] e [tex]\boxed{A_2=\dfrac{l^2}{8}} [/tex] . Desta forma segue que:
[tex]\qquad \boxed{\text{Área do quadrado maior}}= 4A_1+4A_2=8\dfrac{l^2}{8}=\boxed{l^2} [/tex] ;
[tex]\qquad \boxed{\text{Área do quadrado menor}}= 4A_2=4\dfrac{l^2}{8}=\boxed{\dfrac{l^2}{2}} \, .[/tex]
A primeira área já conhecíamos, pois sabemos que [tex]l[/tex] é o comprimento dos lados do quadrado maior; mas a segunda área é a que permite concluir que a área do quadrado interno é metade da área do quadrado inicial.
Podemos agora resolver o problema; para isso, sejam Área 1, Área 2 e Área 3 as áreas dos três quadrados, conforme indica a figura abaixo.
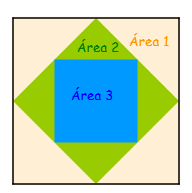
Note que, se [tex]A[/tex] é a área do quadrado maior, então:
Área 1[tex]=A\\[/tex]
Área 2[tex]=\dfrac{A}{2}\\[/tex]
Área 3[tex]=\dfrac{\frac{A}{2}}{2}=\dfrac{A}{4}.[/tex]
Como em cada bandeirinha a área colorida de azul é Área 3 e a área da bandeirinha é Área 1, temos que um quarto de cada bandeirinha está colorida de azul.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
