.Probleminha: Olimpíadas

Problema
(Indicado a partir do 1º ano do E. M.)

---

Uma escola realizou duas olimpíadas neste ano: a Olimpíada de Matemática e a Olimpíada de História. Com relação à participação dos [tex]940[/tex] alunos da escola nessas duas olimpíadas, sabe-se que:

• [tex]15\%[/tex] dos alunos não participaram de nenhuma das olimpíadas;
• [tex]455[/tex] participaram da Olimpíada de Matemática;
• [tex]424[/tex] participaram da Olimpíada de História.

Calcule o número total de alunos da escola que participaram das duas olimpíadas.

Solução

---

Primeiro calculamos quanto é [tex]15\%[/tex] de [tex]940[/tex]: [tex]\dfrac{15}{100}\times 940 =141[/tex].
Assim, [tex]141[/tex] alunos não participaram de olimpíadas.
Desta forma, [tex]940-141=799[/tex] alunos participaram de alguma olimpíada.
Vamos denotar por [tex]x[/tex] a quantidade de alunos da escola que participaram das duas Olimpíadas e vamos construir um diagrama de Venn para visualizarmos melhor os dados que temos.

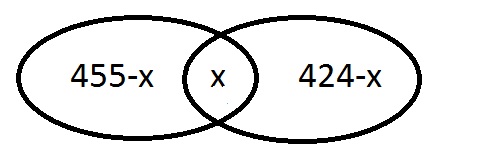
Observando o diagrama, obtemos a equação [tex]\boxed{455+424-x=799} \, [/tex], cuja solução é [tex]\boxed{x=80} \, .[/tex]
Portanto, [tex]\fcolorbox{black}{#eee0e5}{$80$}[/tex] alunos participaram das duas olimpíadas realizadas pela escola.

---

Solução elaborada pelos Moderadores do Blog.