 |
Apresentaremos aqui algumas definições e propriedades básicas de Conjuntos e utilizaremos diagramas de Venn para ilustrá-las.
|
Um pouco da linguagem de conjuntos
Uma das formas de se representar um conjunto é utilizando diagramas conhecidos por “diagramas de Venn“. De modo geral, um diagrama é uma representação visual simplificada de um determinado conceito ou ideia; nos diagramas de Venn os conjuntos são representados por linhas fechadas contidas em um plano e seus elementos são dispostos na região do plano limitada pela linha. Os diagramas de Venn têm o nome de seu criador, John Venn – matemático e lógico inglês que viveu de 1834 a 1923.
Por exemplo, na figura abaixo temos a representação dos conjuntos [tex]A = \{2, 4, 7, 9, 12\}[/tex], [tex]B = \{2, 5, 6, 9, 10, 15\}[/tex] e [tex]S =\{2, 4, 5, 6, 7, 8, 9, 10, 12, 15\}[/tex] por meio de diagramas de Venn.
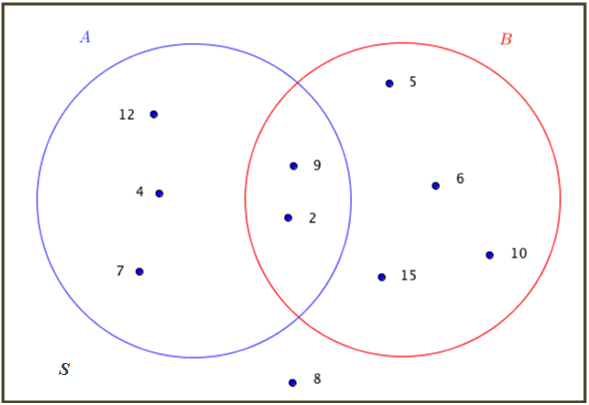
Esse tipo de representação pode ajudar a entender melhor as operações entre conjuntos, bem como perceber algumas de suas propriedades.
Vamos utilizar diagramas de Venn para ilustrar e tentar entender algumas definições que aparecem de vez em quando nos nossos estudos.
I – Relação de Pertinência
Os objetos que compõem um conjunto são denominados “elementos” do conjunto em questão. A pertinência a um conjunto é usualmente indicada pelo símbolo [tex]\in[/tex] e, a não pertinência, pelo símbolo [tex]\notin [/tex]. Assim:
► a notação [tex]x \in X[/tex] significa que “o objeto [tex]x[/tex] é elemento do conjunto [tex]X[/tex]”;
► a notação [tex]b \notin B[/tex] indica que “o objeto [tex]b[/tex] não é elemento do conjunto [tex]B[/tex]”.
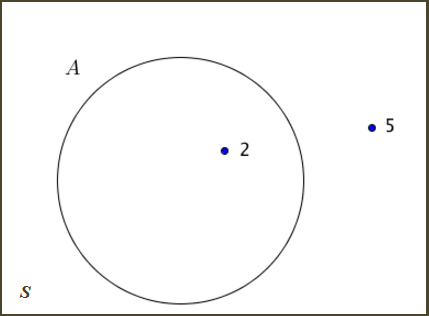
Dessa forma, utilizando a figura abaixo, podemos usar as expressões:
● [tex]2 \in A[/tex] para indicar que o número [tex]2[/tex] é elemento do conjunto [tex]A[/tex].
● [tex]5 \notin A[/tex] para indicar que o número [tex]5[/tex] não é elemento do conjunto [tex]A[/tex].
Dependendo do contexto, o símbolo [tex]\in[/tex] pode ser lido como
– “é elemento de”;
– “é membro de”;
– “está em”, “pertence a”;
e a sua negação [tex]\notin [/tex] pode ser lida como
– “não é elemento de”;
– “não é membro de”;
– “não está em”, “não pertence a”.
II – Relação de Inclusão
Se todo elemento de um conjunto [tex]A[/tex] é também elemento de um conjunto [tex]B[/tex], dizemos que [tex]A[/tex] está contido em [tex]B[/tex] (ou que [tex]A[/tex] é subconjunto de [tex]B[/tex]) e utilizamos a notação [tex]A \subset B[/tex].
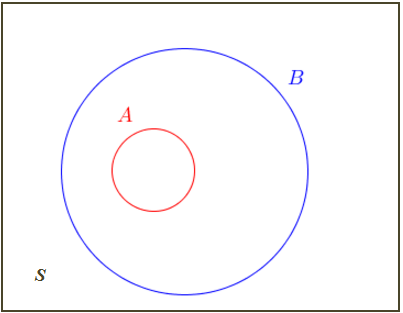
Com relação à figura acima, podemos escrever que:
► [tex]A \subset B[/tex], para indicar que [tex]A[/tex] é subconjunto de [tex]B[/tex];
► [tex]A \subset S[/tex], para indicar que [tex]A[/tex] é subconjunto de [tex]S[/tex];
► [tex]B \subset S[/tex], para indicar que [tex]B[/tex] é subconjunto de [tex]S[/tex];
► [tex]A \subset B \subset S[/tex], para indicar as três inclusões.
III – Operações com conjuntos
Assim como podemos somar e multiplicar números, existem algumas operações que podemos fazer com conjuntos. Dessa forma, é possível criarmos novos conjuntos a partir de conjuntos dados utilizando essas operações, dentre as quais destacamos: a união, a interseção e a diferença. Vamos relembrar como efetuar cada uma delas e ilustrá-las com diagramas de Venn.
União de conjuntos
A união de dois conjuntos [tex]A[/tex] e [tex]B[/tex] é o conjunto indicado por [tex]A \cup B[/tex] e formado por todos os elementos de [tex]A[/tex] e por todos os elementos de [tex]B[/tex].
Em símbolos:
[tex]\qquad A \cup B = \{ x \, ; \, x \in A \,\textrm{ou}\, x \in B\}[/tex].
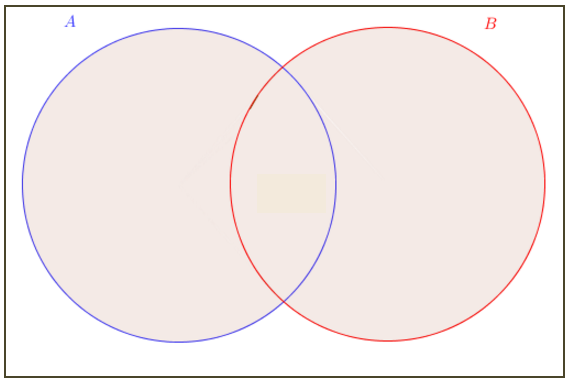
Na figura acima, [tex]A[/tex] e [tex]B[/tex] são representados pelos círculos e [tex]A \cup B[/tex] é a parte sombreada.
Interseção de conjuntos
A interseção de dois conjuntos [tex]A[/tex] e [tex]B[/tex] é o conjunto indicado por [tex]A \cap B[/tex] e formado pelos elementos comuns a [tex]A[/tex] e a [tex]B[/tex].
Assim:
[tex]\qquad A \cap B = \{ x \, ; \, x \in A \,\textrm{e}\, x \in B\}[/tex].
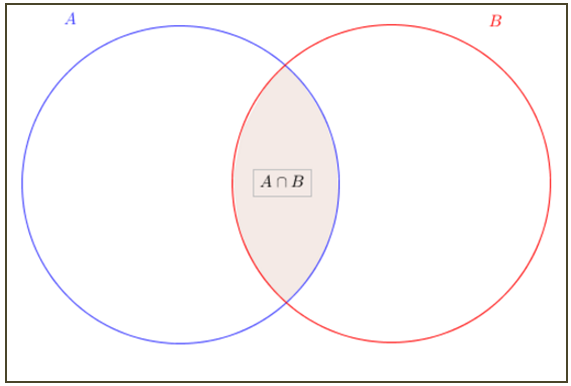
Na figura acima, [tex]A[/tex] e [tex]B[/tex] são também representados pelos círculos e [tex]A \cap B[/tex] é a parte sombreada.
Diferença de conjuntos
A diferença entre dois conjuntos [tex]A[/tex] e [tex]B[/tex] é o conjunto indicado por [tex]A – B[/tex] e formado pelos elementos de [tex]A[/tex] que não são elementos de [tex]B[/tex].
Dessa forma:
[tex]\qquad A – B = \{ x \, ; \, x \in A \,\textrm{e}\, x \notin B\}[/tex].
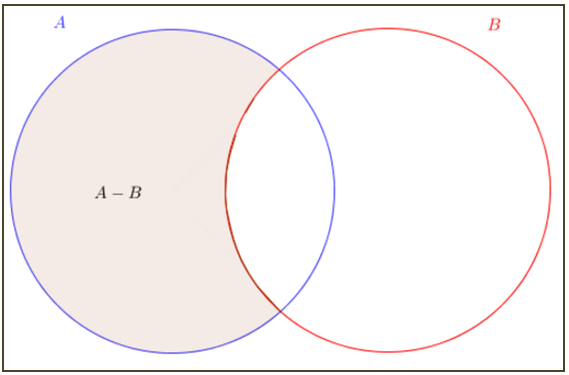
Na figura acima, uma vez mais, [tex]A[/tex] e [tex]B[/tex] são representados pelos círculos e [tex]A – B[/tex] é a parte sombreada.
Quando temos [tex]A[/tex] e [tex]B[/tex] conjuntos tais que [tex]B \subset A[/tex], a diferença [tex]A – B[/tex] é denominada o complementar de [tex]B[/tex], com relação a [tex]A[/tex] e indicada como [tex]\complement^A_B [/tex]. Particularmente, se [tex]S[/tex] é um conjunto que contém todos os conjuntos envolvidos em uma determinada discussão, a diferença [tex]S – X[/tex] é dita, simplesmente, o complementar de [tex]X[/tex] e é indicada com a notação [tex]\complement X [/tex] ou [tex]\overline{X}[/tex].
Podemos utilizar diagramas de Venn para ajudar no entendimento de propriedades dessas três operações definidas. Abaixo vamos apresentar quatro dessas propriedades e ilustrar duas delas.
IV – Algumas propriedades importantes
Sejam [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] conjuntos quaisquer; então valem as propriedades abaixo.
► Comutatividade da união
[tex]\qquad (A \cup B) = (B \cup A)[/tex]
►Comutatividade da interseção
[tex]\qquad (A \cap B) = (B \cap A)[/tex]
► Distributividade da união em relação à interseção
[tex]\qquad A \cup (B \cap C) = (A \cup B) \cap (A \cup C)[/tex]
►Distributividade da interseção em relação à união
[tex]\qquad A \cap (B \cup C) = (A \cap B) \cup (A \cap C)[/tex]
Se [tex]A[/tex] e [tex]B[/tex] forem subconjuntos de um conjunto [tex]S[/tex], então valem também as duas próximas propriedades.
►Leis de De Morgan
[tex]\qquad \overline{A} \cup \overline{B} = \overline{A \cap B}[/tex]
[tex]\qquad \overline{A} \cap \overline{B} = \overline{A \cup B}[/tex]
Observação: Em função das comutatividades da união e da interseção, as duas distributividades podem ser assim reescritas:
[tex]\qquad (B \cap C) \cup A = (B \cup A) \cap (C \cup A)[/tex];
[tex]\qquad (B \cup C) \cap A = (B \cap A) \cup (C \cap A)[/tex].
Ilustrações
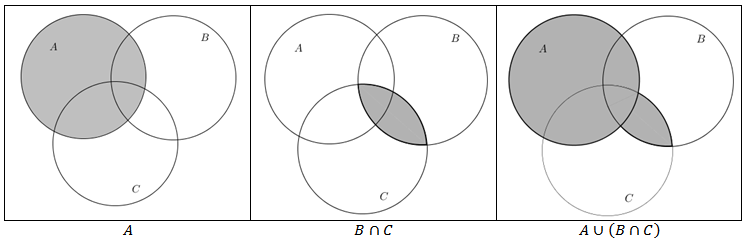
(1) Os próximos diagramas ilustram a propriedade distributiva [tex] A \cup (B \cap C) = (A \cup B) \cap (A \cup C)[/tex].
∎ Para obtermos a respectiva representação do conjunto [tex] A \cup (B \cap C)[/tex] seguimos os seguintes passos:
▪ Sombreamos o conjunto [tex]A[/tex];
▪ Sombreamos a interseção [tex]B \cap C[/tex];
▪ Sombreamos a união de [tex]A[/tex] e a interseção [tex]B \cap C[/tex].
∎ Para obtermos a respectiva representação do conjunto [tex] (A \cup B) \cap (A \cup C)[/tex] seguimos os seguintes passos:
▪ Sombreamos os conjuntos [tex]A[/tex] e [tex]B[/tex] para ilustrar a união [tex] A \cup B[/tex];
▪ Sombreamos os conjuntos [tex]A[/tex] e [tex]C[/tex] para ilustrar a união [tex] A \cup C[/tex];
▪ Fizemos a sobreposição das representações das uniões [tex]A \cup B \, [/tex] e [tex]A \cup C \, [/tex] e sombreamos a interseção.
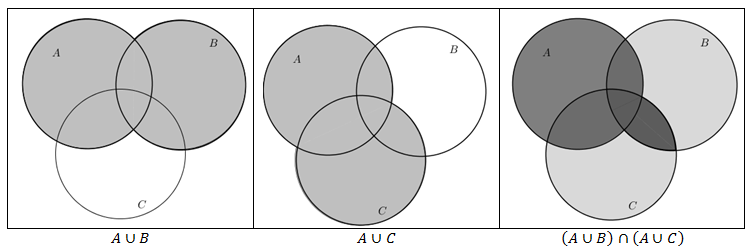
Observem que os sombreamentos finais dos dois passo a passos ilustram a igualdade em questão.
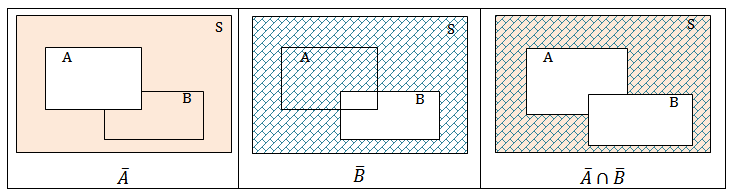
(2) Consideraremos [tex]A[/tex] e [tex]B[/tex] subconjuntos de um conjunto [tex]S[/tex]. Os próximos diagramas ilustram a segunda lei de De Morgan [tex]\overline{A} \cap \overline{B} = \overline{A \cup B}[/tex].
∎ Para a representação do conjunto [tex] \overline{A} \cap \overline{B}[/tex] seguimos os seguintes passos:
▪ Colorimos o complementar de [tex] A[/tex], com relação a [tex] S[/tex];
▪ Colorimos o complementar de[tex]B[/tex], com relação a [tex] S[/tex];
▪ Colorimos a interseção de [tex]\overline A[/tex] e [tex]\overline B[/tex].
∎ Para obtermos a representação do conjunto [tex]\overline{A \cup B}[/tex] seguimos os seguintes passos:
▪ Colorimos a união dos conjuntos [tex]A[/tex] e [tex]B[/tex];
▪ Colorimos o complementar da união [tex] A \cap B[/tex].
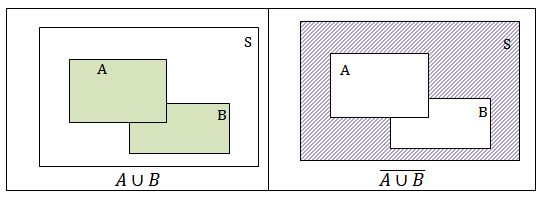
Observem que as regiões coloridas dos últimos diagramas dos dois passo a passos ilustram a igualdade em questão.
Para quem gosta de resolver exercícios …
V – Exercícios
1. Represente conjuntos pelos diagramas de Venn e ilustre as propriedades que não foram ilustradas.
[tex]\qquad (A \cup B) = (B \cup A)[/tex]
[tex]\qquad (A \cap B) = (B \cap A)[/tex]
[tex]\qquad A \cup (B \cap C) = (A \cup B) \cap (A \cup C)[/tex]
[tex]\qquad A \cap (B \cup C) = (A \cap B) \cup (A \cap C)[/tex]
[tex]\qquad \overline{A} \cup \overline{B} = \overline{A \cap B}[/tex]
2. Quais das seguintes igualdades são verdadeiras?
(a) [tex](A \cup B) \cap (A \cup C) = A \cup (B \cap C)[/tex]
(b) [tex]A \cup B = (A \cap \overline{B}) \cup B[/tex]
(c) [tex]\overline{A} \cap B = A \cup B[/tex]
(d) [tex](\overline{A \cup B}) \cap C = \overline{A} \cap \overline{B} \cap C[/tex]
(e) [tex](A \cap B) \cap (\overline{B} \cap C) = \emptyset[/tex]
(f) [tex](A \cap B) \cup (A \cap \overline{B}) = A[/tex]
Equipe COM – OBMEP
